Difference between revisions of "Aufgaben:Exercise 2.08Z: Addition and Multiplication in GF(2 power 3)"
From LNTwww
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Definition und Eigenschaften von Reed–Solomon–Codes }} [[File:|right|]] ===Fragebogen=== <quiz display=simpl…“) |
|||
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} |
| + | [[File:P_ID2536__KC_Z_2_8.png|right|frame|$\rm GF(2^3)$: Incomplete addition and multiplication tables]] | ||
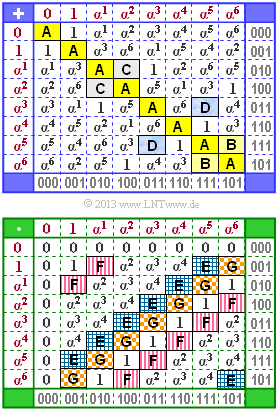
| + | The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields $($highlighted in color$)$ should be completed. | ||
| + | The elements are given both | ||
| + | *in the exponent representation $($with red lettering, left and above$)$ and | ||
| − | + | *in the coefficient representation (gray lettering, right and below). | |
| − | |||
| + | From this assignment one can already recognize the underlying irreducible polynomial $p(\alpha)$. | ||
| − | + | *Additions $($and subtractions$)$ are best done in the coefficient representation $($or with polynomials firmly linked to it$)$. | |
| + | |||
| + | *For multiplications, however, the exponential representation is more convenient. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes| "Definition and Properties of Reed-Solomon Codes"]]. | ||
| + | |||
| + | * However, reference is also made to the chapter [[Channel_Coding/Extension_Field| "Extension Field"]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What element does the "$\rm A$" stand for in the addition table? |
| − | |type=" | + | |type="()"} |
| − | - | + | + $\rm A = 0$, |
| − | + | - $\rm A = 1$, | |
| + | - $\rm A = \alpha^1$, | ||
| + | {What element does the "$\rm B$" stand for in the addition table? | ||
| + | |type="()"} | ||
| + | - $\rm B = 0$, | ||
| + | - $\rm B = 1$, | ||
| + | + $\rm B = \alpha^1$. | ||
| − | { | + | {What element does the "$\rm C$" stand for in the addition table? |
| − | |type=" | + | |type="()"} |
| − | $\alpha$ = | + | - $\rm C = \alpha^2$, |
| + | - $\rm C = \alpha^3$, | ||
| + | + $\rm C = \alpha^4$. | ||
| + | {What element does the "$\rm D$" stand for in the addition table? | ||
| + | |type="()"} | ||
| + | + $\rm D = \alpha^2$, | ||
| + | - $\rm D = \alpha^3$, | ||
| + | - $\rm D = \alpha^4$. | ||
| + | {What assignments apply in the multiplication table? | ||
| + | |type="[]"} | ||
| + | + $\rm E = \alpha^5$, | ||
| + | + $\rm F = \alpha^1$, | ||
| + | + $\rm G = \alpha^6$. | ||
| + | {What irreducible polynomial underlies these tables? | ||
| + | |type="()"} | ||
| + | - $p(\alpha) = \alpha^2 + \alpha + 1$, | ||
| + | - $p(\alpha) = \alpha^3 + \alpha^2 + 1$, | ||
| + | + $p(\alpha) = \alpha^3 + \alpha + 1$. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Adding any element of an extension field based on $\rm GF(2)$ to itself always yields $0$, as can be easily seen from the coefficient representation, for example: |
| − | '''2 | + | :$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 |
| − | '''3 | + | \hspace{0.05cm}.$$ |
| − | '''4 | + | |
| − | '''5 | + | *That is: $\rm A$ stands for the zero element ⇒ <u>Solution 1</u>. |
| − | + | ||
| − | + | ||
| − | {{ | + | |
| + | '''(2)''' $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ <u>Solution 3</u>: | ||
| + | :$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *One could have found this result more simply, since in each row and column each element occurs exactly once. | ||
| + | |||
| + | *After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' $\rm C$ is the result of the sum $\alpha^1 +\alpha^2$ ⇒ <u>Solution 3</u>: | ||
| + | :$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ <u>Solution 1</u>: | ||
| + | :$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' <u>All proposed solutions</u> are correct, as can be seen from row 2 (multiplication with the "identity element"): | ||
| + | [[File:P_ID2573__KC_Z_2_8e.png|right|frame|$\rm GF(2^3)$: Complete addition and multiplication tables]] | ||
| + | *The complete tables for addition and multiplication are shown opposite. | ||
| + | |||
| + | *Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve. | ||
| + | |||
| + | |||
| + | '''(6)''' Correct here is the <u>proposed solution 3</u>: | ||
| + | * All polynomials are indeed irreducible. However, one needs a degree-3 polynomial for $\rm GF(2^3)$. | ||
| + | |||
| + | *The third proposed solution results from the relation | ||
| + | :$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$ | ||
| + | {{ML-Fuß}} | ||
| − | |||
| − | ^]] | + | [[Category:Channel Coding: Exercises|^2.3 Reed–Solomon Codes^]] |
Latest revision as of 16:40, 10 October 2022
The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields $($highlighted in color$)$ should be completed.
The elements are given both
- in the exponent representation $($with red lettering, left and above$)$ and
- in the coefficient representation (gray lettering, right and below).
From this assignment one can already recognize the underlying irreducible polynomial $p(\alpha)$.
- Additions $($and subtractions$)$ are best done in the coefficient representation $($or with polynomials firmly linked to it$)$.
- For multiplications, however, the exponential representation is more convenient.
Hints:
- This exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- However, reference is also made to the chapter "Extension Field".
Questions
Solution
(1) Adding any element of an extension field based on $\rm GF(2)$ to itself always yields $0$, as can be easily seen from the coefficient representation, for example:
- $$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$
- That is: $\rm A$ stands for the zero element ⇒ Solution 1.
(2) $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ Solution 3:
- $$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$
- One could have found this result more simply, since in each row and column each element occurs exactly once.
- After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column.
(3) $\rm C$ is the result of the sum $\alpha^1 +\alpha^2$ ⇒ Solution 3:
- $$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$
(4) $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ Solution 1:
- $$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$
(5) All proposed solutions are correct, as can be seen from row 2 (multiplication with the "identity element"):
- The complete tables for addition and multiplication are shown opposite.
- Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve.
(6) Correct here is the proposed solution 3:
- All polynomials are indeed irreducible. However, one needs a degree-3 polynomial for $\rm GF(2^3)$.
- The third proposed solution results from the relation
- $$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$