Difference between revisions of "Aufgaben:Exercise 2.08Z: Addition and Multiplication in GF(2 power 3)"
From LNTwww
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} | {{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} | ||
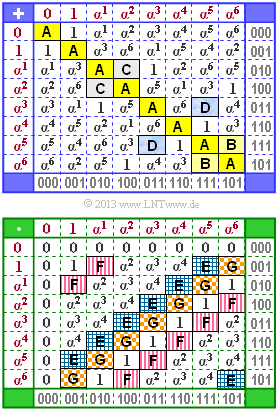
| − | [[File:P_ID2536__KC_Z_2_8.png|right|frame|$\rm GF(2^3)$: Incomplete addition and multiplication tables]] | + | [[File:P_ID2536__KC_Z_2_8.png|right|frame|$\rm GF(2^3)$: Incomplete addition and multiplication tables]] |
| − | The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields (highlighted in color) should be completed. | + | The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields $($highlighted in color$)$ should be completed. |
| − | The elements are given both in the exponent representation (with red lettering, left and above | + | The elements are given both |
| + | *in the exponent representation $($with red lettering, left and above$)$ and | ||
| − | *Additions (and subtractions) are best done in the coefficient representation (or with | + | *in the coefficient representation (gray lettering, right and below). |
| − | *For multiplications, however, the | + | |
| + | |||
| + | From this assignment one can already recognize the underlying irreducible polynomial $p(\alpha)$. | ||
| + | |||
| + | *Additions $($and subtractions$)$ are best done in the coefficient representation $($or with polynomials firmly linked to it$)$. | ||
| + | |||
| + | *For multiplications, however, the exponential representation is more convenient. | ||
| Line 16: | Line 23: | ||
Hints: | Hints: | ||
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes| "Definition and Properties of Reed-Solomon Codes"]]. |
| − | * However, reference is also made to the chapter [[Channel_Coding/Extension_Field| "Extension Field"]]. | + | |
| + | * However, reference is also made to the chapter [[Channel_Coding/Extension_Field| "Extension Field"]]. | ||
| Line 23: | Line 31: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What element does the $\rm A$ stand for in the addition table? | + | {What element does the "$\rm A$" stand for in the addition table? |
|type="()"} | |type="()"} | ||
+ $\rm A = 0$, | + $\rm A = 0$, | ||
| Line 29: | Line 37: | ||
- $\rm A = \alpha^1$, | - $\rm A = \alpha^1$, | ||
| − | {What element does the $\rm B$ stand for in the addition table? | + | {What element does the "$\rm B$" stand for in the addition table? |
|type="()"} | |type="()"} | ||
- $\rm B = 0$, | - $\rm B = 0$, | ||
| Line 35: | Line 43: | ||
+ $\rm B = \alpha^1$. | + $\rm B = \alpha^1$. | ||
| − | {What element does the $\rm C$ stand for in the addition table? | + | {What element does the "$\rm C$" stand for in the addition table? |
|type="()"} | |type="()"} | ||
- $\rm C = \alpha^2$, | - $\rm C = \alpha^2$, | ||
| Line 41: | Line 49: | ||
+ $\rm C = \alpha^4$. | + $\rm C = \alpha^4$. | ||
| − | {What element does the $\rm D$ stand for in the addition table? | + | {What element does the "$\rm D$" stand for in the addition table? |
|type="()"} | |type="()"} | ||
+ $\rm D = \alpha^2$, | + $\rm D = \alpha^2$, | ||
| Line 62: | Line 70: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Adding any element of an extension field based on $\rm GF(2)$ to itself always yields $0$, as can be easily seen from the coefficient representation, for example: | + | '''(1)''' Adding any element of an extension field based on $\rm GF(2)$ to itself always yields $0$, as can be easily seen from the coefficient representation, for example: |
:$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 | :$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | That is: $\rm A$ stands for the zero element ⇒ <u>Solution 1</u>. | + | *That is: $\rm A$ stands for the zero element ⇒ <u>Solution 1</u>. |
| − | '''(2)''' $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ <u>Solution 3</u>: | + | '''(2)''' $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ <u>Solution 3</u>: |
:$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$ | :$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$ | ||
| − | *One could have found this result more simply, since in each row and column each element occurs exactly once. | + | *One could have found this result more simply, since in each row and column each element occurs exactly once. |
| − | *After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column. | + | |
| + | *After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column. | ||
| − | '''(3)''' $\rm C$ is the result of the sum | + | '''(3)''' $\rm C$ is the result of the sum $\alpha^1 +\alpha^2$ ⇒ <u>Solution 3</u>: |
:$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$ | :$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$ | ||
| − | '''(4)''' $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ <u>Solution 1</u>: | + | '''(4)''' $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ <u>Solution 1</u>: |
:$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 | :$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 89: | Line 98: | ||
| − | '''(5)''' <u>All proposed solutions</u> are correct, as can be seen from row 2 (multiplication with the identity element): | + | '''(5)''' <u>All proposed solutions</u> are correct, as can be seen from row 2 (multiplication with the "identity element"): |
| − | [[File:P_ID2573__KC_Z_2_8e.png|right|frame|$\rm GF(2^3)$: Complete addition and multiplication tables]] | + | [[File:P_ID2573__KC_Z_2_8e.png|right|frame|$\rm GF(2^3)$: Complete addition and multiplication tables]] |
*The complete tables for addition and multiplication are shown opposite. | *The complete tables for addition and multiplication are shown opposite. | ||
| − | *Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve. | + | |
| + | *Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve. | ||
| − | '''(6)''' Correct here is the <u>proposed solution 3</u>: | + | '''(6)''' Correct here is the <u>proposed solution 3</u>: |
| − | * All polynomials are indeed irreducible. However, one needs a degree 3 polynomial for $\rm GF(2^3)$. | + | * All polynomials are indeed irreducible. However, one needs a degree-3 polynomial for $\rm GF(2^3)$. |
| + | |||
*The third proposed solution results from the relation | *The third proposed solution results from the relation | ||
:$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
Latest revision as of 16:40, 10 October 2022
The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields $($highlighted in color$)$ should be completed.
The elements are given both
- in the exponent representation $($with red lettering, left and above$)$ and
- in the coefficient representation (gray lettering, right and below).
From this assignment one can already recognize the underlying irreducible polynomial $p(\alpha)$.
- Additions $($and subtractions$)$ are best done in the coefficient representation $($or with polynomials firmly linked to it$)$.
- For multiplications, however, the exponential representation is more convenient.
Hints:
- This exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- However, reference is also made to the chapter "Extension Field".
Questions
Solution
(1) Adding any element of an extension field based on $\rm GF(2)$ to itself always yields $0$, as can be easily seen from the coefficient representation, for example:
- $$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$
- That is: $\rm A$ stands for the zero element ⇒ Solution 1.
(2) $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ Solution 3:
- $$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$
- One could have found this result more simply, since in each row and column each element occurs exactly once.
- After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column.
(3) $\rm C$ is the result of the sum $\alpha^1 +\alpha^2$ ⇒ Solution 3:
- $$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$
(4) $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ Solution 1:
- $$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$
(5) All proposed solutions are correct, as can be seen from row 2 (multiplication with the "identity element"):
- The complete tables for addition and multiplication are shown opposite.
- Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve.
(6) Correct here is the proposed solution 3:
- All polynomials are indeed irreducible. However, one needs a degree-3 polynomial for $\rm GF(2^3)$.
- The third proposed solution results from the relation
- $$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$