Difference between revisions of "Aufgaben:Exercise 2.10Z: Noise with DSB-AM and SSB-AM"
m |
m |
||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Single-Sideband_Modulation |
}} | }} | ||
| − | [[File:EN_Mod_Z_2_9_c.png|right|frame|Shared block diagram for DSB-AM and SSB-AM]] | + | [[File:EN_Mod_Z_2_9_c.png|right|frame|Shared block diagram for <br>DSB-AM and SSB-AM]] |
| − | Now the influence of noise on the sink-to-noise ratio $10 · \lg ρ_v$ for both DSB–AM and SSB–AM transmission will be compared. The illustration shows the underlying block diagram. | + | Now the influence of noise on the sink-to-noise power ratio $10 · \lg ρ_v$ for both $\rm DSB–AM$ and $\rm SSB–AM$ transmission will be compared. The illustration shows the underlying block diagram. |
The differences between the two system variants are highlighted in red on the image, namely the modulator (DSB or SSB) as well as the dimensionless constant | The differences between the two system variants are highlighted in red on the image, namely the modulator (DSB or SSB) as well as the dimensionless constant | ||
| − | :$$ K = \left\{ \begin{array}{c} 2/\alpha_{\rm K} \\ 4/\alpha_{\rm K} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{ | + | :$$ K = \left\{ \begin{array}{c} 2/\alpha_{\rm K} \\ 4/\alpha_{\rm K} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\rm DSB} \hspace{0.05cm}, \\ {\rm SSB} \hspace{0.05cm} \\ \end{array}$$ |
| − | of the receiver-side carrier signal $z_{\rm E}(t) = K · \cos(ω_{\rm T} · t)$, which is assumed to be frequency and phase synchronous with the carrier signal $z(t)$ at the transmitter. | + | of the receiver-side carrier signal $z_{\rm E}(t) = K · \cos(ω_{\rm T} · t)$, which is assumed to be frequency and phase synchronous with the carrier signal $z(t)$ at the transmitter. |
| − | The system | + | The system characteristics |
| + | *frequency-independent channel transmission factor $α_{\rm K}$, | ||
| + | *transmission power $P_{\rm S}$, | ||
| + | *one–sided noise power density $N_{\rm 0}$, | ||
| + | *bandwidth $B_{\rm NF}$ of the source signal, | ||
| + | |||
| + | |||
| + | captured by the shared performance parameter are labelled in green: | ||
:$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ | :$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ | ||
| Line 18: | Line 25: | ||
Further note: | Further note: | ||
* The cosine signal $q(t)$ with frequency $B_{\rm NF}$ stands for a source signal with bandwidth $B_{\rm NF}$ composed of multiple frequencies. | * The cosine signal $q(t)$ with frequency $B_{\rm NF}$ stands for a source signal with bandwidth $B_{\rm NF}$ composed of multiple frequencies. | ||
| − | * DSB–AM with carrier is parameterized by | + | *The relationship between the transmission power $P_{\rm S}$ and the power $P_{q}$ of the source signal depends, among other things, on the modulation method. |
| − | * The frequency-independent channel transmission factor $α_{\rm K}$ is balanced by the constant $K$ | + | * "DSB–AM with carrier" is parameterized by the modulation depth $m = A_{\rm N}/A_{\rm T}$, <br>while "SSB-AM" is determined by the sideband-to-carrier ratio $μ = A_{\rm N}/(2 · A_{\rm T})$. |
| − | * The sink SNR can thus be given as follows $(T_0$ indicates the period of the source signal$)$: | + | * The frequency-independent channel transmission factor $α_{\rm K}$ is balanced by the constant $K$, so that in the noise-free case $(N_0 = 0)$, <br>the sink signal $v(t)$ matches the source signal $q(t)$. |
| − | :$$ \rho_{v } = \frac{P_{q}}{P_{\varepsilon }}\hspace{0.5cm}{\rm | + | * The sink SNR can thus be given as follows $(T_0$ indicates the period of the source signal$)$: |
| + | :$$ \rho_{v } = \frac{P_{q}}{P_{\varepsilon }}\hspace{0.5cm}{\rm with}\hspace{0.5cm} P_{q} = \frac{1}{T_{\rm 0}}\cdot\int_{0}^{ T_{\rm 0}} {q^2(t)}\hspace{0.1cm}{\rm d}t, \hspace{0.5cm}P_{\varepsilon} = \int_{-B_{\rm NF}}^{ +B_{\rm NF}} \hspace{-0.1cm}{\it \Phi_{\varepsilon}}(f)\hspace{0.1cm}{\rm d}f\hspace{0.05cm}.$$ | ||
| Line 27: | Line 35: | ||
| − | + | Hints: | |
| − | *This exercise belongs to the chapter [[Modulation_Methods/Single-Sideband_Modulation|Single- | + | *This exercise belongs to the chapter [[Modulation_Methods/Single-Sideband_Modulation|"Single-Sideband Modulation"]]. |
| − | *Particular reference is made to the | + | *Particular reference is made to the section [[Modulation_Methods/Single-Sideband_Modulation#Sideband-to-carrier_ratio|"Sideband-to-carrier ratio"]]. |
| − | *The results for DSB–AM can be found | + | *The results for DSB–AM can be found in the section [[Modulation_Methods/Synchronous_Demodulation#Sink_SNR_and_the_performance_parameter|"Sink SNR and the performance parameter"]]. |
| Line 42: | Line 50: | ||
- Envelope demodulation. | - Envelope demodulation. | ||
| − | {Which relationship holds between the quantities $ρ_v$ and $ξ$ for <u> | + | {Which relationship holds between the quantities $ρ_v$ and $ξ$ for <u>double-sideband AM without carrier</u> $(m → ∞)$? |
|type="[]"} | |type="[]"} | ||
- $ρ_v = 2 · ξ$. | - $ρ_v = 2 · ξ$. | ||
| Line 48: | Line 56: | ||
- $ρ_v = ξ/2$. | - $ρ_v = ξ/2$. | ||
| − | {Which relationship holds between $ρ_v$ and $ξ$ for <u> | + | {Which relationship holds between $ρ_v$ and $ξ$ for <u>single-sideband AM without carrier</u> as $(μ → ∞)$? |
|type="[]"} | |type="[]"} | ||
- $ρ_v = 2 · ξ$. | - $ρ_v = 2 · ξ$. | ||
| Line 54: | Line 62: | ||
- $ρ_v = ξ/2$. | - $ρ_v = ξ/2$. | ||
| − | {Let $ξ = 10^4$. Calculate the sink-to-noise ratio of <u> | + | {Let $ξ = 10^4$. Calculate the sink-to-noise ratio of <u>double-sideband AM</u> for modulation depths $m = 0.5$ and $m = 1$. |
|type="{}"} | |type="{}"} | ||
$m = 0.5\text{:} \ \ 10 · \lg \ ρ_v \ = \ $ { 30.46 3% } $\ \rm dB$ | $m = 0.5\text{:} \ \ 10 · \lg \ ρ_v \ = \ $ { 30.46 3% } $\ \rm dB$ | ||
$m = 1.0\text{:} \ \ 10 · \lg \ ρ_v \ = \ $ { 35.23 3% } $\ \rm dB$ | $m = 1.0\text{:} \ \ 10 · \lg \ ρ_v \ = \ $ { 35.23 3% } $\ \rm dB$ | ||
| − | { | + | {Further let $ξ = 10^4$. Calculate the sink-to-noise ratio of <u>single-sideband AM</u> for the parameters $μ = 0.354$ and $μ = 0.707$. |
|type="{}"} | |type="{}"} | ||
$μ = 0.354\text{:} \ \ \ 10 · \lg \ ρ_v \ = \ $ { 30.46 3% } $\ \rm dB$ | $μ = 0.354\text{:} \ \ \ 10 · \lg \ ρ_v \ = \ $ { 30.46 3% } $\ \rm dB$ | ||
| Line 69: | Line 77: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' We are dealing with a <u>synchronous demodulator</u>. <u>Answer 1</u> is correct. |
| + | |||
| + | '''(2)''' <u>Answer 2</u> is correct: | ||
| + | *For DSB–AM without a carrier, $P_{\rm S} = P_q/2$. This is simultaneously the power of the useful component of the sink signal $v(t)$. | ||
| + | *The power-spectral density ${\it Φ}_ε(f)$ of the $v(t)$ noise component results from the convolution: | ||
| + | [[File:P_ID1048__Mod_Z_2_9_b.png|right|frame|Noise power density <br>in double-sideband AM]] | ||
| + | [[File:P_ID1049__Mod_Z_2_9_c.png|right|frame|Noise power density <br>in upper-sideband AM]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
:$${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{1}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$ | :$${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{1}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$ | ||
| − | * | + | *The expression $\big[$ ... $\big]$ describes the power-spectral density of a cosine signal with the signal amplitude $K = 2$. |
| − | * | + | *The correction of channel attenuation is considered with $1/α_K^2$ . |
| − | * | + | *Thus, taking ${\it \Phi}_n(f) = N_0/2$ into account, we get: |
:$${\it \Phi}_\varepsilon(f) = \frac{N_0}{\alpha_{\rm K}^2} | :$${\it \Phi}_\varepsilon(f) = \frac{N_0}{\alpha_{\rm K}^2} | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \int_{-B_{\rm NF}}^{+B_{\rm NF}} {{\it \Phi}_\varepsilon(f) }\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$ | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \int_{-B_{\rm NF}}^{+B_{\rm NF}} {{\it \Phi}_\varepsilon(f) }\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$ | ||
| − | * | + | *From this, it follows for the the signal-to-noise power ratio $\rm (SNR)$: |
:$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}\hspace{0.15cm}\underline { = \xi} \hspace{0.05cm}.$$ | :$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}\hspace{0.15cm}\underline { = \xi} \hspace{0.05cm}.$$ | ||
| − | + | '''(3)''' <u>Answer 2</u> is correct: | |
| − | '''(3)''' | + | *In contrast to DSB, $P_S = P_q/4$ holds for SSB, as well as |
| − | * | ||
:$${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{4}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$ | :$${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{4}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$ | ||
| − | * | + | *Taking $B_{\rm HF} = B_{\rm NF}$ into account (see adjacent diagram for USB modulation), we now get: |
:$${\it \Phi}_\varepsilon(f) = \frac{2 \cdot N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \frac{4 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$ | :$${\it \Phi}_\varepsilon(f) = \frac{2 \cdot N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \frac{4 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$ | ||
| − | * | + | *This means: When without carrier, single-sideband modulation demonstrates the same noise behaviour as DSB-AM. |
| − | '''(4)''' | + | '''(4)''' Assuming a cosine carrier with amplitude $A_{\rm T}$ and a similarly cosine source signal $q(t)$, we get for DSB with carrier: |
:$$ s(t) = \big (q(t) + A_{\rm T}\big ) \cdot \cos( \omega_{\rm T} \cdot t) | :$$ s(t) = \big (q(t) + A_{\rm T}\big ) \cdot \cos( \omega_{\rm T} \cdot t) | ||
= A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t) + \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}+ \omega_{\rm N}) \cdot t \big)+ \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}- \omega_{\rm N}) \cdot t\big)\hspace{0.05cm}.$$ | = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t) + \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}+ \omega_{\rm N}) \cdot t \big)+ \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}- \omega_{\rm N}) \cdot t\big)\hspace{0.05cm}.$$ | ||
| − | * | + | *The transmission power is thus given by |
:$$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + 2 \cdot \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.05cm}.$$ | :$$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + 2 \cdot \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.05cm}.$$ | ||
| − | * | + | *Taking $P_q = A_{\rm N}^2/2$ and $m = A_{\rm N}/A_{\rm T}$ into account, this can also be written as: |
:$$P_{\rm S}= \frac{A_{\rm N}^2}{4} \cdot \left[ 1 + \frac{2 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{2} \cdot \left[ 1 + {2 }/{m^2}\right]\hspace{0.05cm}.$$ | :$$P_{\rm S}= \frac{A_{\rm N}^2}{4} \cdot \left[ 1 + \frac{2 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{2} \cdot \left[ 1 + {2 }/{m^2}\right]\hspace{0.05cm}.$$ | ||
| − | * | + | *With the noise power $P_ε$ according to subtask '''(2)''' we thus obtain: |
:$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}\cdot (1 + 2/m^2)}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{2 }/{m^2}} \hspace{0.05cm}.$$ | :$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}\cdot (1 + 2/m^2)}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{2 }/{m^2}} \hspace{0.05cm}.$$ | ||
| − | * | + | *And in logarithmic representation: |
:$$ 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{2 }/{m^2}}\right] \hspace{0.05cm}.$$ | :$$ 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{2 }/{m^2}}\right] \hspace{0.05cm}.$$ | ||
:$$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 0.5) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (9) \hspace{0.15cm}\underline {= 30.46\, {\rm dB}}$$ | :$$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 0.5) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (9) \hspace{0.15cm}\underline {= 30.46\, {\rm dB}}$$ | ||
| Line 115: | Line 124: | ||
| − | '''(5)''' | + | '''(5)''' In "SSB–AM" there is only one sideband. |
| − | * | + | *Therefore, considering the sideband-to-carrier ratio $μ = A_{\rm N}/(2A_{\rm T})$ gives: |
:$$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = {A_{\rm N}^2}/{8} \cdot \big[ 1 + {4 \cdot A_{\rm T}^2}/{A_{\rm N}^2}\big] = {P_q}/{4} \cdot \big[ 1 + {1 }/{\mu^2}\big] \hspace{0.05cm}.$$ | :$$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = {A_{\rm N}^2}/{8} \cdot \big[ 1 + {4 \cdot A_{\rm T}^2}/{A_{\rm N}^2}\big] = {P_q}/{4} \cdot \big[ 1 + {1 }/{\mu^2}\big] \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, with the noise power from subtask '''(3)''' we obtain: |
:$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{4 \cdot P_{\rm S}\cdot (1 + 1/\mu^2)}{4 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{1 }/{\mu^2}}\hspace{0.3cm} | :$$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{4 \cdot P_{\rm S}\cdot (1 + 1/\mu^2)}{4 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{1 }/{\mu^2}}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\big[{1 +{1 }/{\mu^2}}\big] \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\big[{1 +{1 }/{\mu^2}}\big] \hspace{0.05cm}.$$ | ||
| − | * | + | *So we get the same result with SSB-AM as in DSB-AM with a modulation depth of $m = \sqrt{2} · μ$. From this, it further follows: |
| − | + | :$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm SSB,} \hspace{0.1cm}\mu = {0.5}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm DSB,} \hspace{0.1cm}m=0.5) \hspace{0.15cm}\underline {=30.46\,{\rm dB}},$$ | |
| − | :$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm | + | :$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm SSB,} \hspace{0.1cm}\mu = {1.0}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm DSB,} \hspace{0.1cm}m=1.0) \hspace{0.15cm}\underline {=35.23\,{\rm dB}}\hspace{0.05cm}.$$ |
| − | :$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:13, 9 April 2022
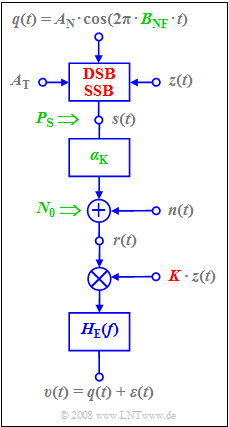
Now the influence of noise on the sink-to-noise power ratio $10 · \lg ρ_v$ for both $\rm DSB–AM$ and $\rm SSB–AM$ transmission will be compared. The illustration shows the underlying block diagram.
The differences between the two system variants are highlighted in red on the image, namely the modulator (DSB or SSB) as well as the dimensionless constant
- $$ K = \left\{ \begin{array}{c} 2/\alpha_{\rm K} \\ 4/\alpha_{\rm K} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\rm DSB} \hspace{0.05cm}, \\ {\rm SSB} \hspace{0.05cm} \\ \end{array}$$
of the receiver-side carrier signal $z_{\rm E}(t) = K · \cos(ω_{\rm T} · t)$, which is assumed to be frequency and phase synchronous with the carrier signal $z(t)$ at the transmitter.
The system characteristics
- frequency-independent channel transmission factor $α_{\rm K}$,
- transmission power $P_{\rm S}$,
- one–sided noise power density $N_{\rm 0}$,
- bandwidth $B_{\rm NF}$ of the source signal,
captured by the shared performance parameter are labelled in green:
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
Further note:
- The cosine signal $q(t)$ with frequency $B_{\rm NF}$ stands for a source signal with bandwidth $B_{\rm NF}$ composed of multiple frequencies.
- The relationship between the transmission power $P_{\rm S}$ and the power $P_{q}$ of the source signal depends, among other things, on the modulation method.
- "DSB–AM with carrier" is parameterized by the modulation depth $m = A_{\rm N}/A_{\rm T}$,
while "SSB-AM" is determined by the sideband-to-carrier ratio $μ = A_{\rm N}/(2 · A_{\rm T})$. - The frequency-independent channel transmission factor $α_{\rm K}$ is balanced by the constant $K$, so that in the noise-free case $(N_0 = 0)$,
the sink signal $v(t)$ matches the source signal $q(t)$. - The sink SNR can thus be given as follows $(T_0$ indicates the period of the source signal$)$:
- $$ \rho_{v } = \frac{P_{q}}{P_{\varepsilon }}\hspace{0.5cm}{\rm with}\hspace{0.5cm} P_{q} = \frac{1}{T_{\rm 0}}\cdot\int_{0}^{ T_{\rm 0}} {q^2(t)}\hspace{0.1cm}{\rm d}t, \hspace{0.5cm}P_{\varepsilon} = \int_{-B_{\rm NF}}^{ +B_{\rm NF}} \hspace{-0.1cm}{\it \Phi_{\varepsilon}}(f)\hspace{0.1cm}{\rm d}f\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Single-Sideband Modulation".
- Particular reference is made to the section "Sideband-to-carrier ratio".
- The results for DSB–AM can be found in the section "Sink SNR and the performance parameter".
Questions
Solution
(2) Answer 2 is correct:
- For DSB–AM without a carrier, $P_{\rm S} = P_q/2$. This is simultaneously the power of the useful component of the sink signal $v(t)$.
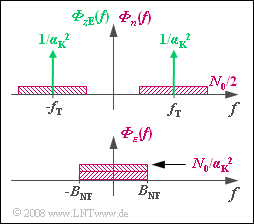
- The power-spectral density ${\it Φ}_ε(f)$ of the $v(t)$ noise component results from the convolution:
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{1}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
- The expression $\big[$ ... $\big]$ describes the power-spectral density of a cosine signal with the signal amplitude $K = 2$.
- The correction of channel attenuation is considered with $1/α_K^2$ .
- Thus, taking ${\it \Phi}_n(f) = N_0/2$ into account, we get:
- $${\it \Phi}_\varepsilon(f) = \frac{N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \int_{-B_{\rm NF}}^{+B_{\rm NF}} {{\it \Phi}_\varepsilon(f) }\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
- From this, it follows for the the signal-to-noise power ratio $\rm (SNR)$:
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}\hspace{0.15cm}\underline { = \xi} \hspace{0.05cm}.$$
(3) Answer 2 is correct:
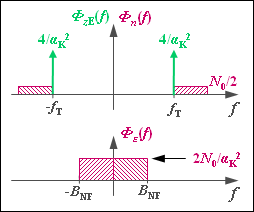
- In contrast to DSB, $P_S = P_q/4$ holds for SSB, as well as
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{4}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
- Taking $B_{\rm HF} = B_{\rm NF}$ into account (see adjacent diagram for USB modulation), we now get:
- $${\it \Phi}_\varepsilon(f) = \frac{2 \cdot N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \frac{4 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
- This means: When without carrier, single-sideband modulation demonstrates the same noise behaviour as DSB-AM.
(4) Assuming a cosine carrier with amplitude $A_{\rm T}$ and a similarly cosine source signal $q(t)$, we get for DSB with carrier:
- $$ s(t) = \big (q(t) + A_{\rm T}\big ) \cdot \cos( \omega_{\rm T} \cdot t) = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t) + \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}+ \omega_{\rm N}) \cdot t \big)+ \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}- \omega_{\rm N}) \cdot t\big)\hspace{0.05cm}.$$
- The transmission power is thus given by
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + 2 \cdot \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.05cm}.$$
- Taking $P_q = A_{\rm N}^2/2$ and $m = A_{\rm N}/A_{\rm T}$ into account, this can also be written as:
- $$P_{\rm S}= \frac{A_{\rm N}^2}{4} \cdot \left[ 1 + \frac{2 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{2} \cdot \left[ 1 + {2 }/{m^2}\right]\hspace{0.05cm}.$$
- With the noise power $P_ε$ according to subtask (2) we thus obtain:
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}\cdot (1 + 2/m^2)}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{2 }/{m^2}} \hspace{0.05cm}.$$
- And in logarithmic representation:
- $$ 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{2 }/{m^2}}\right] \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 0.5) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (9) \hspace{0.15cm}\underline {= 30.46\, {\rm dB}}$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 1.0) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (3) \hspace{0.15cm}\underline {= 35.23\, {\rm dB} \hspace{0.05cm}}.$$
(5) In "SSB–AM" there is only one sideband.
- Therefore, considering the sideband-to-carrier ratio $μ = A_{\rm N}/(2A_{\rm T})$ gives:
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = {A_{\rm N}^2}/{8} \cdot \big[ 1 + {4 \cdot A_{\rm T}^2}/{A_{\rm N}^2}\big] = {P_q}/{4} \cdot \big[ 1 + {1 }/{\mu^2}\big] \hspace{0.05cm}.$$
- Thus, with the noise power from subtask (3) we obtain:
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{4 \cdot P_{\rm S}\cdot (1 + 1/\mu^2)}{4 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{1 }/{\mu^2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\big[{1 +{1 }/{\mu^2}}\big] \hspace{0.05cm}.$$
- So we get the same result with SSB-AM as in DSB-AM with a modulation depth of $m = \sqrt{2} · μ$. From this, it further follows:
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm SSB,} \hspace{0.1cm}\mu = {0.5}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm DSB,} \hspace{0.1cm}m=0.5) \hspace{0.15cm}\underline {=30.46\,{\rm dB}},$$
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm SSB,} \hspace{0.1cm}\mu = {1.0}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm DSB,} \hspace{0.1cm}m=1.0) \hspace{0.15cm}\underline {=35.23\,{\rm dB}}\hspace{0.05cm}.$$