Difference between revisions of "Aufgaben:Exercise 2.11: Reed-Solomon Decoding according to "Erasures""
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel}} |
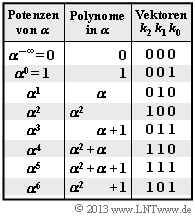
| − | [[File:P_ID2542__KC_A_2_11_neu.png|right|frame|${\rm GF}(2^3)$, | + | [[File:P_ID2542__KC_A_2_11_neu.png|right|frame|${\rm GF}(2^3)$, represented as powers, polynomials and coefficient vectors]] |
| − | + | We consider here an encoding and decoding system corresponding to the [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel#Block_diagram_and_requirements_for_RS_fault_detection| "graph"]] in the theory section for this chapter. To be noted: | |
| − | * | + | * The Reed–Solomon code is given by the generator matrix $\mathbf{G}$ and the parity-check matrix $\mathbf{H}$ where all elements are from the Galois field $\rm GF(2^3) \ \backslash \ \{0\}$ : |
:$${ \boldsymbol{\rm G}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | :$${ \boldsymbol{\rm G}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 18: | Line 18: | ||
\end{pmatrix} \hspace{0.05cm}.$$ | \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | * | + | * All code symbols $c_i ∈ \{0, \, 1, \, \alpha, \, \alpha^2, \, \alpha^3, \, \alpha^4, \, \alpha^5, \, \alpha^6\}$ are represented by $m = 3$ bits and transmitted via the erasure channel (highlighted in green in the graphic) $(m$ BEC$)$ . A code symbol is already marked as an erasure (<i>Erasure</i> ) $\rm E$ if one of the three associated bits is uncertain. |
| − | * | + | * The <i>code word finder</i> (CWF) has the exercise of generating the regenerated codeword $\underline{z}$ from the partially erased received word $\underline{y}$ . It must be ensured that the result $\underline{z}$ is indeed a valid Reed–Solomon codeword. |
| − | * | + | * If the received word $\underline{y}$ contains too many erasures, the decoder outputs a message of the type "symbol cannot be decoded". So no attempt is made to estimate the codeword. If $\underline{z}$ is output, this is also correct: $\underline{z} = \underline{c}$. |
| − | * | + | * The sought information value $\underline{v} = \underline{u}$ results from the inverse coder function $\underline{v} = {\rm enc}^{-1}(\underline{z})$. With the generator matrix $\mathbf{G}$ this can be realized as follows: |
:$$\underline{c} = {\rm enc}(\underline{u}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u} \cdot {\boldsymbol{\rm G}} | :$$\underline{c} = {\rm enc}(\underline{u}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u} \cdot {\boldsymbol{\rm G}} | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{z} = {\rm enc}(\underline{v}) | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{z} = {\rm enc}(\underline{v}) | ||
| Line 34: | Line 34: | ||
| − | + | Hints: | |
| − | * | + | * This exercise refers to the chapter [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel| "Reed–Solomon Decoding at the Erasure Channel"]]. |
| − | * | + | * Regarding the <i>code word finder</i>, we refer in particular to the pages [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel#Procedure_using_the_RSC_as_an_example_.287.2C_3.2C_5. 298| "procedure"]] and [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel#Solution_of_the_matrix_equations_using_the_example_of_the_RSC_.287.2C_3.2C_5.298| "Solution of the matrix equations"]]. |
| − | * | + | * All calculations are to be performed in $\rm GF(2^3)$ . The upper graph describes their $q = 8$ elements in power , polynomial and coefficient vector representation. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Specify the code parameters of the present Reed–Solomon code. |
|type="{}"} | |type="{}"} | ||
$n \ = \ ${ 7 } | $n \ = \ ${ 7 } | ||
| Line 49: | Line 49: | ||
$d_{\rm min} \ = \ ${ 4 } | $d_{\rm min} \ = \ ${ 4 } | ||
| − | { | + | {Can the received vector $\underline{y} = (0, \, 0, \, 0,\, 0, \, 0, \, 0, \, {\rm E})$ be decoded?? |
|type="()"} | |type="()"} | ||
| − | + | + | + YES. |
| − | - | + | - NO. |
| − | { | + | {Can the received vector $\underline{y} = (\rm E, \, E, \, 1, \, 1, \, 1, \, 1, \, 1)$ be decoded? |
|type="()"} | |type="()"} | ||
| − | + | + | + YES. |
| − | - | + | - NO. |
| − | { | + | {What is the result of decoding $\underline{y} = (\rm E, \, E, \, E, \, 0, \, 1, \, \alpha, \, 0)$? |
|type="()"} | |type="()"} | ||
- $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0$. | - $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0$. | ||
+ $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3$. | + $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3$. | ||
- $z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3$. | - $z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3$. | ||
| − | - | + | - The decoding does not lead to any result. |
| − | { | + | {What is the result of decoding $\underline{y} = (\rm E, \, E, \, E, \, 0, \, 1, \, \alpha, \, E)$? |
|type="()"} | |type="()"} | ||
- $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0, \ z_6 = 1$. | - $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0, \ z_6 = 1$. | ||
- $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3, \ z_6 = 1$. | - $z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3, \ z_6 = 1$. | ||
- $z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3, \ z_6 = 1$. | - $z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3, \ z_6 = 1$. | ||
| − | + | + | + The decoding does not lead to any result. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The number of columns of the parity-check matrix $\mathbf{H}$ indicates the code length: $n \ \underline{= 7}$. |
| − | * | + | *The same result is obtained if we assume the order $q = 8$ of the Galois field. For the Reed–Solomon codes $n = q - 1$ is valid. |
| − | * | + | *The number of rows of the parity-check matrix is equal to $n - k = 3 \ \Rightarrow \ k \ \underline{= 4}$. |
| − | * | + | *Of all Reed–Solomon codes, the [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes#Singleton_bound_and_minimum_distance| "Singleton bound"]] is satisfied ⇒ $d_{\rm min} = n - k + 1 \ \underline{= 4}$. |
| − | * | + | *Thus, it is the Reed–Solomon code $(7, \, 4, \, 4)_8$. |
| − | '''(2)''' | + | '''(2)''' Decoding is certainly possible as long as the number $e$ of extinctions is smaller than the minimum distance $d_{\rm min}$. This condition is fulfilled here ⇒ <b><u>YES</u></b>. |
| − | * | + | *Since the null word is allowed in all RS codes and every other codeword contains at least four symbols not equal to "$0$", it is already certain without calculation that the null word was sent. |
| − | * | + | *The formal calculation confirms this result: |
:$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} = | :$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 106: | Line 106: | ||
| − | '''(3)''' | + | '''(3)''' Again $e = 2$ is smaller than $d_{\rm min} = 4$ ⇒ <b><u>YES</u></b>. |
| − | * | + | *Since $(1, \, 1, \, 1, \, 1, \, 1, \, 1, \, 1)$ is also a valid codeword, we expect $z_0 = 1$ und $z_1 = 1$ in the formal verification. |
:$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | :$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 143: | Line 143: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *In this calculation, we varied between the polynomial representation and the coefficient representation on the data side. Thus the system of equations reads: |
:$$\begin{pmatrix} | :$$\begin{pmatrix} | ||
(001) + (010) \\ | (001) + (010) \\ | ||
| Line 173: | Line 173: | ||
\end{pmatrix}\hspace{0.05cm}.$$ | \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | * | + | *The second form is obtained by substituting the third row from the modulo $2$ sum of rows 2 and 3. |
| − | * | + | *From the last row now follows $z_1 = 1$ and the rows 1 and 2 are then: |
:$$(1)\hspace{0.3cm}z_0 + (010) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (011)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm},$$ | :$$(1)\hspace{0.3cm}z_0 + (010) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (011)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm},$$ | ||
:$$(2)\hspace{0.3cm}z_0 + (100) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (101)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm}. $$ | :$$(2)\hspace{0.3cm}z_0 + (100) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (101)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm}. $$ | ||
| − | * | + | *Both equations lead to the same result $z_0 = 1, \ z_1 = 1$. The decoding is successful. |
| − | '''(4)''' | + | '''(4)''' Decoding happens on following steps: |
:$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | :$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 238: | Line 238: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *We now replace row 2 with the modulo $2$ sum of rows 1 and 2, and row 3 with the modulo $2$ sum of rows 1 and 3: |
:$$\begin{pmatrix} | :$$\begin{pmatrix} | ||
(001) &(010) &(100)\\ | (001) &(010) &(100)\\ | ||
| Line 256: | Line 256: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *From the last row follows $z_1 + z_2 = 0 \ \Rightarrow \ z_2 = z_1$. Substituting into the second row of this matrix equation we get: |
:$$\big[(110) + (010)\big] \cdot z_1 = (100) \cdot z_1 = (111) \hspace{0.2cm} \Rightarrow \hspace{0.2cm} | :$$\big[(110) + (010)\big] \cdot z_1 = (100) \cdot z_1 = (111) \hspace{0.2cm} \Rightarrow \hspace{0.2cm} | ||
\alpha^2 \cdot z_1 = \alpha^5\hspace{0.2cm}\Rightarrow \hspace{0.2cm} | \alpha^2 \cdot z_1 = \alpha^5\hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| Line 262: | Line 262: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *With this result follows from the first matrix row: |
:$$z_0 + \big[(010) + (100)\big] \cdot z_1 = z_0 + (110) \cdot z_1 = (011) $$ | :$$z_0 + \big[(010) + (100)\big] \cdot z_1 = z_0 + (110) \cdot z_1 = (011) $$ | ||
:$$\Rightarrow \hspace{0.2cm} z_0 + \alpha^4 \cdot \alpha^3 = z_0 + 1 = \alpha^3 | :$$\Rightarrow \hspace{0.2cm} z_0 + \alpha^4 \cdot \alpha^3 = z_0 + 1 = \alpha^3 | ||
| Line 268: | Line 268: | ||
z_0 = \alpha^3 + 1 = ( \alpha + 1) +1\hspace{0.15cm} \underline{= \alpha}\hspace{0.05cm}.$$ | z_0 = \alpha^3 + 1 = ( \alpha + 1) +1\hspace{0.15cm} \underline{= \alpha}\hspace{0.05cm}.$$ | ||
| − | * | + | *The correct solution is therefore <u>proposal solution 2</u>. |
| − | '''(5)''' | + | '''(5)''' Correct is <u>proposed solution 4</u>. Reason: |
| − | * | + | * Four information symbols cannot be obtained from the three known symbols $0, \, 1, \, \alpha$. |
| − | * | + | *The $\mathbf{H}$ matrix of this $(7, \, 4, \, 4)_8$ code has exactly $n - k = 3$ rows. |
| − | * | + | *This also means that you have only three equations. But you would need four equations for the unknowns $z_0, \ z_1, \ z_2$ and $z_6$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 23:35, 3 September 2022
We consider here an encoding and decoding system corresponding to the "graph" in the theory section for this chapter. To be noted:
- The Reed–Solomon code is given by the generator matrix $\mathbf{G}$ and the parity-check matrix $\mathbf{H}$ where all elements are from the Galois field $\rm GF(2^3) \ \backslash \ \{0\}$ :
- $${ \boldsymbol{\rm G}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},$$
- $${ \boldsymbol{\rm H}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$
- All code symbols $c_i ∈ \{0, \, 1, \, \alpha, \, \alpha^2, \, \alpha^3, \, \alpha^4, \, \alpha^5, \, \alpha^6\}$ are represented by $m = 3$ bits and transmitted via the erasure channel (highlighted in green in the graphic) $(m$ BEC$)$ . A code symbol is already marked as an erasure (Erasure ) $\rm E$ if one of the three associated bits is uncertain.
- The code word finder (CWF) has the exercise of generating the regenerated codeword $\underline{z}$ from the partially erased received word $\underline{y}$ . It must be ensured that the result $\underline{z}$ is indeed a valid Reed–Solomon codeword.
- If the received word $\underline{y}$ contains too many erasures, the decoder outputs a message of the type "symbol cannot be decoded". So no attempt is made to estimate the codeword. If $\underline{z}$ is output, this is also correct: $\underline{z} = \underline{c}$.
- The sought information value $\underline{v} = \underline{u}$ results from the inverse coder function $\underline{v} = {\rm enc}^{-1}(\underline{z})$. With the generator matrix $\mathbf{G}$ this can be realized as follows:
- $$\underline{c} = {\rm enc}(\underline{u}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u} \cdot {\boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{z} = {\rm enc}(\underline{v}) = \underline{v} \cdot {\boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{v} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm enc}^{-1}(\underline{z}) = \underline{z} \cdot {\boldsymbol{\rm G}}^{\rm T}\hspace{0.05cm}.$$
Hints:
- This exercise refers to the chapter "Reed–Solomon Decoding at the Erasure Channel".
- Regarding the code word finder, we refer in particular to the pages "procedure" and "Solution of the matrix equations".
- All calculations are to be performed in $\rm GF(2^3)$ . The upper graph describes their $q = 8$ elements in power , polynomial and coefficient vector representation.
Questions
Solution
(1) The number of columns of the parity-check matrix $\mathbf{H}$ indicates the code length: $n \ \underline{= 7}$.
- The same result is obtained if we assume the order $q = 8$ of the Galois field. For the Reed–Solomon codes $n = q - 1$ is valid.
- The number of rows of the parity-check matrix is equal to $n - k = 3 \ \Rightarrow \ k \ \underline{= 4}$.
- Of all Reed–Solomon codes, the "Singleton bound" is satisfied ⇒ $d_{\rm min} = n - k + 1 \ \underline{= 4}$.
- Thus, it is the Reed–Solomon code $(7, \, 4, \, 4)_8$.
(2) Decoding is certainly possible as long as the number $e$ of extinctions is smaller than the minimum distance $d_{\rm min}$. This condition is fulfilled here ⇒ YES.
- Since the null word is allowed in all RS codes and every other codeword contains at least four symbols not equal to "$0$", it is already certain without calculation that the null word was sent.
- The formal calculation confirms this result:
- $${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} \alpha^6\\ \alpha^{5}\\ \alpha^{4} \end{pmatrix} \cdot z_6 = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_6 = 0 \hspace{0.05cm}. $$
(3) Again $e = 2$ is smaller than $d_{\rm min} = 4$ ⇒ YES.
- Since $(1, \, 1, \, 1, \, 1, \, 1, \, 1, \, 1)$ is also a valid codeword, we expect $z_0 = 1$ und $z_1 = 1$ in the formal verification.
- $${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \cdot\begin{pmatrix} 1\\ 1\\ 1\\ 1\\ 1 \end{pmatrix}= \begin{pmatrix} \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6\\ \alpha^4 + \alpha^6 + \alpha^1 + \alpha^{3} + \alpha^{5}\\ \alpha^6 + \alpha^2 + \alpha^{5} + \alpha^{1} + \alpha^{4} \end{pmatrix}$$
- $$\Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \begin{pmatrix} (100) + (011) + (110) + (111) + (101)\\ (110) + (101) + (010) + (011) + (111)\\ (101) + (100) + (111) + (010) + (110) \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (010) \end{pmatrix} = \begin{pmatrix} \alpha^3\\ \alpha^6\\ \alpha^1 \end{pmatrix} \hspace{0.05cm}. $$
- In this calculation, we varied between the polynomial representation and the coefficient representation on the data side. Thus the system of equations reads:
- $$\begin{pmatrix} (001) + (010) \\ (001) + (100)\\ (001) + (011) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1 \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (010) \end{pmatrix} \hspace{0.25cm} \Rightarrow \hspace{0.25cm} \begin{pmatrix} (001) + (010) \\ (001) + (100)\\ (000) + (111) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1 \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (111) \end{pmatrix}\hspace{0.05cm}.$$
- The second form is obtained by substituting the third row from the modulo $2$ sum of rows 2 and 3.
- From the last row now follows $z_1 = 1$ and the rows 1 and 2 are then:
- $$(1)\hspace{0.3cm}z_0 + (010) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (011)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm},$$
- $$(2)\hspace{0.3cm}z_0 + (100) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (101)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm}. $$
- Both equations lead to the same result $z_0 = 1, \ z_1 = 1$. The decoding is successful.
(4) Decoding happens on following steps:
- $${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \cdot\begin{pmatrix} 0\\ 1\\ \alpha\\ 0 \end{pmatrix}= \begin{pmatrix} \alpha^4 + \alpha^6\\ \alpha^1 + \alpha^{4}\\ \alpha^5 + \alpha^2 \end{pmatrix}= \begin{pmatrix} (110) + (101)\\ (010) + (110)\\ (111) + (100) \end{pmatrix} = \begin{pmatrix} (011)\\ (100)\\ (011) \end{pmatrix} \hspace{0.05cm},$$
- $${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline {z}_{\rm E}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & \alpha^1 & \alpha^2\\ 1 & \alpha^2 & \alpha^4\\ 1 & \alpha^3 & \alpha^6 \end{pmatrix} \cdot\begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} (001) &(010) &(100)\\ (001) &(100) &(110)\\ (001) &(011) &(101) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}= \begin{pmatrix} (011)\\ (100)\\ (011) \end{pmatrix} \hspace{0.05cm}. $$
- We now replace row 2 with the modulo $2$ sum of rows 1 and 2, and row 3 with the modulo $2$ sum of rows 1 and 3:
- $$\begin{pmatrix} (001) &(010) &(100)\\ (000) &(110) &(010)\\ (000) &(001) &(001) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}= \begin{pmatrix} (011)\\ (111)\\ (000) \end{pmatrix} \hspace{0.05cm}.$$
- From the last row follows $z_1 + z_2 = 0 \ \Rightarrow \ z_2 = z_1$. Substituting into the second row of this matrix equation we get:
- $$\big[(110) + (010)\big] \cdot z_1 = (100) \cdot z_1 = (111) \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha^2 \cdot z_1 = \alpha^5\hspace{0.2cm}\Rightarrow \hspace{0.2cm} z_1 \hspace{0.1cm}\underline{= \alpha^3}\hspace{0.05cm},\hspace{0.2cm}z_2 \hspace{0.1cm}\underline{= \alpha^3} \hspace{0.05cm}. $$
- With this result follows from the first matrix row:
- $$z_0 + \big[(010) + (100)\big] \cdot z_1 = z_0 + (110) \cdot z_1 = (011) $$
- $$\Rightarrow \hspace{0.2cm} z_0 + \alpha^4 \cdot \alpha^3 = z_0 + 1 = \alpha^3 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} z_0 = \alpha^3 + 1 = ( \alpha + 1) +1\hspace{0.15cm} \underline{= \alpha}\hspace{0.05cm}.$$
- The correct solution is therefore proposal solution 2.
(5) Correct is proposed solution 4. Reason:
- Four information symbols cannot be obtained from the three known symbols $0, \, 1, \, \alpha$.
- The $\mathbf{H}$ matrix of this $(7, \, 4, \, 4)_8$ code has exactly $n - k = 3$ rows.
- This also means that you have only three equations. But you would need four equations for the unknowns $z_0, \ z_1, \ z_2$ and $z_6$.