Difference between revisions of "Aufgaben:Exercise 2.11Z: Once again SSB-AM and Envelope Demodulator"
| (20 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Single-Sideband_Modulation |
}} | }} | ||
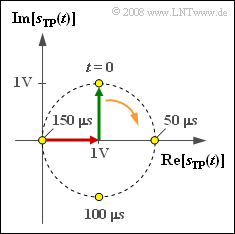
| − | [[File:P_ID1050__Mod_Z_2_10.png|right|frame| | + | [[File:P_ID1050__Mod_Z_2_10.png|right|frame|Equivalent low-pass signal in <br>single-sideband AM]] |
| − | + | The adjacent graph shows the locus curve – i.e., the representation of the equivalent low-pass signal (German: "äquivalentes Tiefpass-Signal" ⇒ subscript: "TP") in the complex plane – for a single-sideband amplitude modulation $\text{(SSB-AM)}$ system. | |
| − | + | It is further given that the carrier frequency is $f_{\rm T} = 100 \ \rm kHz$ and the channel is ideal: | |
:$$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$ | :$$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$ | ||
| − | + | An ideal envelope demodulator is used at the receiver. | |
| − | * | + | |
| + | The following values are used in these exercises: | ||
| + | *the sideband-to-carrier ratio | ||
:$$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$ | :$$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$ | ||
| − | * | + | *the envelope |
:$$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$ | :$$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$ | ||
| − | * | + | *the maximum deviation $τ_{\rm max}$ of the zero crossings between the transmitted signal $s(t)$ and the carrier signal $z(t)$. |
| Line 20: | Line 22: | ||
| − | + | ||
| − | * | + | Hints: |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Single-Sideband_Modulation|Single-sideband Modulation]]. |
| − | * | + | *Particular reference is made to the section [[Modulation_Methods/Single-Sideband_Modulation#Sideband-to-carrier_ratio|Sideband-to-carrier ratio]]. |
| + | *In this exercise, apply the same assumptions as in [[Aufgaben:Exercise_2.11:_Envelope_Demodulation_of_an_ESB_Signal|Exercise 2.11]]. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Find the equivalent low-pass signal $s_{\rm TP}(t)$ in analytical form and choose which statements apply. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - We are dealing with an "upper-sideband amplitude modulation" $\text{(USB-AM)}$. |
| − | + | + | + We are dealing with a "lower-sideband amplitude modulation" $\text{(LSB-AM)}$. |
| − | - | + | - The source signal $q(t)$ is cosine-shaped. |
| − | + | + | + The source signal $q(t)$ is sine-shaped. |
| − | { | + | {Find the amplitude $A_{\rm N}$ and the frequency $f_{\rm N}$ of the source signal. Take into account that we are dealing with a SSB-AM. |
|type="{}"} | |type="{}"} | ||
$A_{\rm N} \ = \ $ { 2 3% } $\ \rm V$ | $A_{\rm N} \ = \ $ { 2 3% } $\ \rm V$ | ||
$f_{\rm N} \ = \ $ { 5 3% } $\ \rm kHz$ | $f_{\rm N} \ = \ $ { 5 3% } $\ \rm kHz$ | ||
| − | { | + | {Which value results for the sideband-to-carrier ratio $μ$? Use this value to describe $s_{\rm TP}(t)$. |
|type="{}"} | |type="{}"} | ||
$μ \ = \ $ { 1 3% } | $μ \ = \ $ { 1 3% } | ||
| − | { | + | {Calculate the time course of the envelope $a(t)$. Which values arise for $t = 50 \ \rm µ s$, $t = 100 \ \rm µ s$ and $t = 150 \ \rm µ s$? |
|type="{}"} | |type="{}"} | ||
$a(t = 50 \ \rm µ s) \hspace{0.32cm} = \ $ { 2 3% } $\ \rm V$ | $a(t = 50 \ \rm µ s) \hspace{0.32cm} = \ $ { 2 3% } $\ \rm V$ | ||
| Line 53: | Line 56: | ||
$a(t = 150 \ \rm µ s) \ = \ $ { 0. } $\ \rm V$ | $a(t = 150 \ \rm µ s) \ = \ $ { 0. } $\ \rm V$ | ||
| − | { | + | {By what time difference $τ_{\rm max}$ (in magnitude) are the zero crossings of $s(t)$ maximally shifted with respect to $z(t)$ ? |
|type="{}"} | |type="{}"} | ||
$τ_{\rm max} \ = \ $ { 2.5 3% } $\ \rm µ s$ | $τ_{\rm max} \ = \ $ { 2.5 3% } $\ \rm µ s$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Answers 2 and 4</u> are correct: |
| − | * | + | *The equivalent low-pass signal is: |
:$$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$ | :$$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$ | ||
| − | * | + | *The locus curve is a circle with its center at $A_{\rm T} = 1 \ \rm V$. |
| − | * | + | *Since the rotation is clockwise, we are dealing with a "LSB-AM". |
| − | * | + | *At the start time $t = 0$, the green pointer is in the direction of the imaginary axis. |
| + | *It follows that the source signal is characterized by $q(t) = A_{\rm N} \cdot \sin(\omega_{\rm N} \cdot t).$ | ||
| + | |||
| + | |||
| + | '''(2)''' For the LSB, only the lower sideband is transmitted, with pointer length $A_{\rm N}/2 = 1 \ \rm V$ . | ||
| + | *This results in $A_{\rm N}\hspace{0.15cm}\underline { = 2 \ \rm V}$. | ||
| + | *For one revolution in the locus, the pointer needs the time $200 \ \rm µ s$. | ||
| + | *The reciprocal of this is the frequency $f_{\rm N}\hspace{0.15cm}\underline { = 5 \ \rm kHz}$. | ||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' According to the definition in the exercise section and the results in subtasks '''(1)''' and '''(2)''', the following holds: |
:$$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | :$$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | ||
| − | + | *Thus, the equivalent low-pass signal can also be written as: | |
| − | :$$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm | + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm here}\hspace{0.15cm}\mu = 1 \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | + | '''(4)''' Splitting the complex exponential function into real and imaginary parts using Euler's theorem, we get: | |
| + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot \big( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\big) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *By applying the "Pythagorean Theorem", this can also be written as: | ||
:$$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = | :$$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = | ||
A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$ | A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$ | ||
| − | + | *The retrieved values when $A_{\rm T} = 1\ \rm V$ are: | |
| − | :$$ a(t = 50\,{\rm | + | :$$ a(t = 50\,{\rm µ s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm µ s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm µ s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$ |
| − | + | *These results can be directly read off the graph in the exercise section. | |
| + | |||
| − | '''(5)''' | + | '''(5)''' A hint for the location of the zero crossings of $s(t)$ with respect to the grid given by the carrier signal $z(t)$ is provided by the phase function $ϕ(t)$. |
| − | * | + | *For the given locus, these can take on values between $±π/2\ (±90^\circ)$ . |
| − | * | + | *For example, these maximum values arise in the region around $t ≈ 150 \ \rm µ s$, since a phase jump occurs there. |
| − | * | + | *The relationship between $τ_{\rm max}$ and $\Delta ϕ_{\rm max}$ is: |
| − | :$$ \tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm | + | :$$ \tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm µ s} \hspace{0.15cm}\underline {= 2.5\,{\rmµ s}} \hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 99: | Line 109: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.4 Single Sideband Amplitude Modulation^]] |
Latest revision as of 14:45, 17 November 2022
The adjacent graph shows the locus curve – i.e., the representation of the equivalent low-pass signal (German: "äquivalentes Tiefpass-Signal" ⇒ subscript: "TP") in the complex plane – for a single-sideband amplitude modulation $\text{(SSB-AM)}$ system.
It is further given that the carrier frequency is $f_{\rm T} = 100 \ \rm kHz$ and the channel is ideal:
- $$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$
An ideal envelope demodulator is used at the receiver.
The following values are used in these exercises:
- the sideband-to-carrier ratio
- $$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$
- the envelope
- $$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$
- the maximum deviation $τ_{\rm max}$ of the zero crossings between the transmitted signal $s(t)$ and the carrier signal $z(t)$.
Hints:
- This exercise belongs to the chapter Single-sideband Modulation.
- Particular reference is made to the section Sideband-to-carrier ratio.
- In this exercise, apply the same assumptions as in Exercise 2.11.
Questions
Solution
- The equivalent low-pass signal is:
- $$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$
- The locus curve is a circle with its center at $A_{\rm T} = 1 \ \rm V$.
- Since the rotation is clockwise, we are dealing with a "LSB-AM".
- At the start time $t = 0$, the green pointer is in the direction of the imaginary axis.
- It follows that the source signal is characterized by $q(t) = A_{\rm N} \cdot \sin(\omega_{\rm N} \cdot t).$
(2) For the LSB, only the lower sideband is transmitted, with pointer length $A_{\rm N}/2 = 1 \ \rm V$ .
- This results in $A_{\rm N}\hspace{0.15cm}\underline { = 2 \ \rm V}$.
- For one revolution in the locus, the pointer needs the time $200 \ \rm µ s$.
- The reciprocal of this is the frequency $f_{\rm N}\hspace{0.15cm}\underline { = 5 \ \rm kHz}$.
(3) According to the definition in the exercise section and the results in subtasks (1) and (2), the following holds:
- $$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$
- Thus, the equivalent low-pass signal can also be written as:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm here}\hspace{0.15cm}\mu = 1 \hspace{0.05cm}.$$
(4) Splitting the complex exponential function into real and imaginary parts using Euler's theorem, we get:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot \big( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\big) \hspace{0.05cm}.$$
- By applying the "Pythagorean Theorem", this can also be written as:
- $$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$
- The retrieved values when $A_{\rm T} = 1\ \rm V$ are:
- $$ a(t = 50\,{\rm µ s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm µ s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm µ s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$
- These results can be directly read off the graph in the exercise section.
(5) A hint for the location of the zero crossings of $s(t)$ with respect to the grid given by the carrier signal $z(t)$ is provided by the phase function $ϕ(t)$.
- For the given locus, these can take on values between $±π/2\ (±90^\circ)$ .
- For example, these maximum values arise in the region around $t ≈ 150 \ \rm µ s$, since a phase jump occurs there.
- The relationship between $τ_{\rm max}$ and $\Delta ϕ_{\rm max}$ is:
- $$ \tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm µ s} \hspace{0.15cm}\underline {= 2.5\,{\rmµ s}} \hspace{0.05cm}.$$