Difference between revisions of "Aufgaben:Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
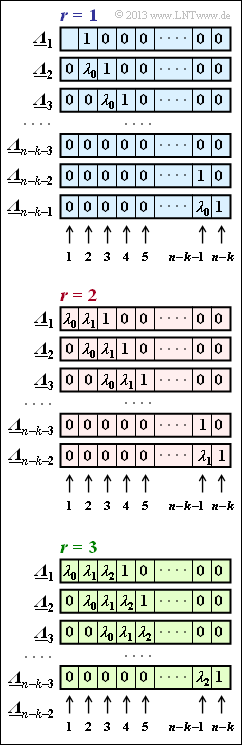
[[File:P_ID2553__KC_A_2_12_neu.png|right|frame|ELP assignment schemes for $r = 1, \ r = 2, \ r = 3$]] | [[File:P_ID2553__KC_A_2_12_neu.png|right|frame|ELP assignment schemes for $r = 1, \ r = 2, \ r = 3$]] | ||
| − | We analyze the Peterson algorithm detailed in the section [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| "Procedure for | + | We analyze the Peterson algorithm detailed in the section [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| "Procedure for Bounded Distance Decoding"]]. Assumed is the Reed–Solomon code with parameters $n = 7, \ k = 4$ and $d_{\rm min} = 4$, where all code symbols come from $\rm GF(2^3)$ and all arithmetic operations are consequently to be performed in $\rm GF(2^3)$ as well. |
The parity-check matrix of this code is: | The parity-check matrix of this code is: | ||
| Line 12: | Line 12: | ||
\end{pmatrix} \hspace{0.05cm}.$$ | \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | In [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD|"Step $\rm (A)$"]] the decoding algorithm considered here, the syndrome $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ must be computed. For the received word | + | # In [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD|"Step $\rm (A)$"]] of the decoding algorithm considered here, the syndrome $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ must be computed. |
| + | # For the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$, the syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$, as in the [[Aufgaben:Exercise_2.12Z:_Reed-Solomon_Syndrome_Calculation|Exercise 2.12Z]] yet to be shown. | ||
| + | # After that the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28D.29 :_Final_error_correction|"ELP coefficient vectors"]] be set up and evaluated according to the adjacent figure, where the assignment depends on whether one assumes $r = 1, \ r = 2$ or $r = 3$ symbol errors in the received word. | ||
| + | # If all equations ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ are satisfied for the assumed symbol error count $r$, then the received word $\underline{y}$ actually has exactly $r$ symbol errors. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Hints: | ||
| + | * The exercise refers to the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error correction according to Reed–Solomon coding"]]. | ||
| + | *"ELP" stands for "Error Locator Polynomial". | ||
| − | + | *You can take the further steps from the theory part: | |
| − | + | :* Step $\rm (C)$: [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28C.29:_Localization_of_the_error_locations|"Localization of error locations"]], | |
| − | + | :* Step $\rm (D)$: [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28D.29:_Final_error_correction|"Determination of the error values"]]. | |
| − | * | ||
| Line 50: | Line 49: | ||
$l_{\rm max} \ = \ ${ 2 3% } | $l_{\rm max} \ = \ ${ 2 3% } | ||
| − | {The syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$. Is the decoding successful? | + | {The syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$. Is the decoding successful? |
|type="()"} | |type="()"} | ||
+ YES. | + YES. | ||
- NO. | - NO. | ||
| − | {Which symbol was | + | {Which symbol was falsified? |
|type="()"} | |type="()"} | ||
| − | - The symbol 0, | + | - The symbol "0", |
| − | + the symbol 1, | + | + the symbol "1", |
| − | - the symbol 6. | + | - the symbol "6". |
| − | {Specify the value of the | + | {Specify the value of the falsified symbol $e_i ≠ 0$. |
|type="()"} | |type="()"} | ||
- $e_i = \alpha^2$, | - $e_i = \alpha^2$, | ||
| Line 67: | Line 66: | ||
- $e_i = 1$. | - $e_i = 1$. | ||
| − | {The syndrome now | + | {The syndrome be now $\underline{s} = (\alpha^2, \, \alpha^4, \, \alpha^5)$. Does this make the decoding successful? |
|type="()"} | |type="()"} | ||
- YES. | - YES. | ||
| Line 75: | Line 74: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct is the <u>proposed solution 1</u>: | + | '''(1)''' Correct is the <u>proposed solution 1</u>: |
| − | *The considered Reed–Solomon code $(7, \, 4, \, 4)_8$ can correct | + | *The considered Reed–Solomon code $(7, \, 4, \, 4)_8$ can only correct $t = ⌊(d_{\rm min} - 1)/2⌋ = 1$ symbol errors because of $d_{\rm min} = 4$. |
| − | *So only the scheme with blue background is relevant, which is valid for the case that there is exactly one symbol error in the received words $(r = 1)$. | + | |
| + | *So only the scheme with blue background is relevant, which is valid for the case that there is exactly one symbol error in the received words $(r = 1)$. | ||
| − | '''(2)''' According to the graph on the specification page, the vector ${\it \underline{\Lambda}}_l$ here has $L = n - k \ \underline{= 3}$ elements. | + | '''(2)''' According to the graph on the specification page, the vector ${\it \underline{\Lambda}}_l$ here has $L = n - k \ \underline{= 3}$ elements. |
| − | '''(3)''' There are only the two ELP coefficient vectors | + | '''(3)''' There are only the two ELP coefficient vectors ${\it \underline{\Lambda}}_1 = (\lambda_0, \, 1, \, 0)$, ${\it \underline{\Lambda}}_2 = (0, \, \lambda_0, \, 1) \ \Rightarrow \ l_{\rm max} \ \underline{= 2}$. |
| − | '''(4)''' From ${\it \underline{\Lambda}}_1$ and ${\it \underline{\Lambda}}_2$ we get two scalar equations of determination ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for the parameter $\lambda_0$: | + | '''(4)''' From ${\it \underline{\Lambda}}_1$ and ${\it \underline{\Lambda}}_2$ we get two scalar equations of determination ⇒ ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for the parameter $\lambda_0$: |
:$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$ | :$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$ | ||
:$$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$ | :$$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$ | ||
| − | The system | + | The equation system is uniquely solvable ⇒ Answer <u>YES</u>. |
| − | '''(5)''' Using the result of subtask (4) ⇒ $\lambda_0 = \alpha$, we obtain for the | + | '''(5)''' Using the result of subtask '''(4)''' ⇒ $\lambda_0 = \alpha$, we obtain for the error locator polynomial: |
:$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) | :$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) | ||
=x \cdot \big (\alpha + x )$$ | =x \cdot \big (\alpha + x )$$ | ||
:$$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 | :$$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 | ||
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zeros}\hspace{0.05cm},$$ |
:$$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 | :$$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 | ||
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zeros}}\hspace{0.05cm}.$$ |
| − | * | + | *So the symbol at position 1 was falsified ⇒ <u>Solution suggestion 2</u>. |
| − | * | + | |
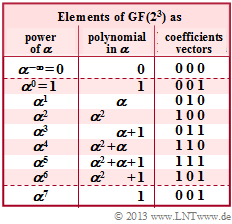
| − | [[File: | + | *Since the calculation in subtask '''(4)''' was done under the condition $r = 1$, all other symbols were transferred correctly: |
| + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representation as powers, polynomials, vectors]] | ||
:$$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$ | :$$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$ | ||
| − | '''(6)''' | + | '''(6)''' From the condition $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}^{\rm T}$ follows |
:$$(0, e_1, 0, 0, 0, 0, 0) \cdot | :$$(0, e_1, 0, 0, 0, 0, 0) \cdot | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 133: | Line 134: | ||
e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$ | e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$ | ||
| − | * | + | *The solution always leads to the result $e_1 = \alpha^3$ ⇒ <u>Answer 2</u>. |
| − | * | + | |
| + | *With the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$, the decoding result is $\underline{z} = (\alpha^1, \, \alpha^3, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$. | ||
| − | '''(7)''' | + | '''(7)''' Analogous to the subtask '''(4)''', the system of equations is now: |
:$$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$ | :$$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$ | ||
:$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$ | :$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$ | ||
| − | * | + | *The two solutions contradict each other. At least two symbols have been falsified during transmission. The decoding fails ⇒ Answer <u>NO</u>. |
| − | * | + | |
| + | *You would now have to start a new attempt according to the red scheme $(r = 2)$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:29, 23 January 2023
We analyze the Peterson algorithm detailed in the section "Procedure for Bounded Distance Decoding". Assumed is the Reed–Solomon code with parameters $n = 7, \ k = 4$ and $d_{\rm min} = 4$, where all code symbols come from $\rm GF(2^3)$ and all arithmetic operations are consequently to be performed in $\rm GF(2^3)$ as well.
The parity-check matrix of this code is:
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$
- In "Step $\rm (A)$" of the decoding algorithm considered here, the syndrome $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ must be computed.
- For the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$, the syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$, as in the Exercise 2.12Z yet to be shown.
- After that the "ELP coefficient vectors" be set up and evaluated according to the adjacent figure, where the assignment depends on whether one assumes $r = 1, \ r = 2$ or $r = 3$ symbol errors in the received word.
- If all equations ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ are satisfied for the assumed symbol error count $r$, then the received word $\underline{y}$ actually has exactly $r$ symbol errors.
Hints:
- The exercise refers to the chapter "Error correction according to Reed–Solomon coding".
- "ELP" stands for "Error Locator Polynomial".
- You can take the further steps from the theory part:
- Step $\rm (C)$: "Localization of error locations",
- Step $\rm (D)$: "Determination of the error values".
Questions
Solution
- The considered Reed–Solomon code $(7, \, 4, \, 4)_8$ can only correct $t = ⌊(d_{\rm min} - 1)/2⌋ = 1$ symbol errors because of $d_{\rm min} = 4$.
- So only the scheme with blue background is relevant, which is valid for the case that there is exactly one symbol error in the received words $(r = 1)$.
(2) According to the graph on the specification page, the vector ${\it \underline{\Lambda}}_l$ here has $L = n - k \ \underline{= 3}$ elements.
(3) There are only the two ELP coefficient vectors ${\it \underline{\Lambda}}_1 = (\lambda_0, \, 1, \, 0)$, ${\it \underline{\Lambda}}_2 = (0, \, \lambda_0, \, 1) \ \Rightarrow \ l_{\rm max} \ \underline{= 2}$.
(4) From ${\it \underline{\Lambda}}_1$ and ${\it \underline{\Lambda}}_2$ we get two scalar equations of determination ⇒ ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for the parameter $\lambda_0$:
- $$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$
- $$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$
The equation system is uniquely solvable ⇒ Answer YES.
(5) Using the result of subtask (4) ⇒ $\lambda_0 = \alpha$, we obtain for the error locator polynomial:
- $${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) =x \cdot \big (\alpha + x )$$
- $$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zeros}\hspace{0.05cm},$$
- $$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zeros}}\hspace{0.05cm}.$$
- So the symbol at position 1 was falsified ⇒ Solution suggestion 2.
- Since the calculation in subtask (4) was done under the condition $r = 1$, all other symbols were transferred correctly:
- $$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$
(6) From the condition $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}^{\rm T}$ follows
- $$(0, e_1, 0, 0, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12} \\ \alpha^5 & \alpha^{10} & \alpha^{15} \\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} \begin{pmatrix} \alpha^4\\ \alpha^5\\ \alpha^6 \end{pmatrix} $$
- $$\Rightarrow \hspace{0.3cm} e_1 \cdot \alpha = \alpha^4\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$
- The solution always leads to the result $e_1 = \alpha^3$ ⇒ Answer 2.
- With the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$, the decoding result is $\underline{z} = (\alpha^1, \, \alpha^3, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$.
(7) Analogous to the subtask (4), the system of equations is now:
- $$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$
- $$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$
- The two solutions contradict each other. At least two symbols have been falsified during transmission. The decoding fails ⇒ Answer NO.
- You would now have to start a new attempt according to the red scheme $(r = 2)$.