Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8

ELP assignment schemes for $r = 1, \ r = 2, \ r = 3$

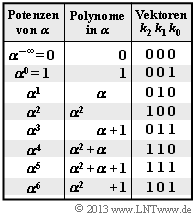
We analyze the Peterson algorithm detailed in the section "Procedure for "Bounded Distance Decoding"" . Assumed is the Reed–Solomon code with parameters $n = 7, \ k = 4$ and $d_{\rm min} = 4$, where all code symbols come from $\rm GF(2^3)$ and all arithmetic operations are consequently to be performed in $\rm GF(2^3)$ as well.

The parity-check matrix of this code is:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

In "Step $\rm (A)$" the decoding algorithm considered here, the syndrome $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ must be computed. For the received word assumed here $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$ the syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$, as in the "Exercise 2.12Z" yet to be shown.

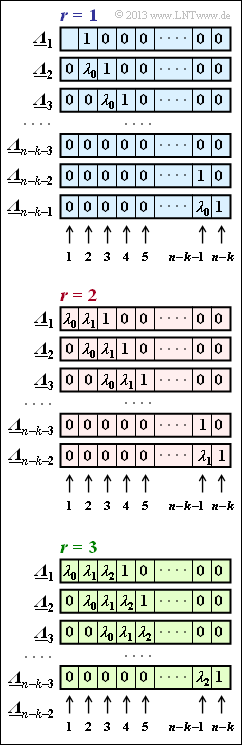
After that the "ELP coefficient vectors" be set up and evaluated according to the adjacent figure, where the assignment depends on whether one assumes $r = 1, \ r = 2$ or $r = 3$ symbol errors in the received word. "ELP" stands for Error Locator Polynomial.

If all equations ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ are satisfied for the assumed symbol error count $r$, then the received word $\underline{y}$ actually has exactly $r$ symbol errors.

You can take the further steps from the theory part:

Step $\rm (C)$: "Localization of error locations",
Step $\rm (D)$: "Determination of the error values".

Hints:

The exercise refers to the chapter "Error correction according to Reed–Solomon coding".

Questions

Solution

(1) Correct is the proposed solution 1:

The considered Reed–Solomon code $(7, \, 4, \, 4)_8$ can correct only $t = ⌊(d_{\rm min} - 1)/2⌋ = 1$ symbol errors because of $d_{\rm min} = 4$.
So only the scheme with blue background is relevant, which is valid for the case that there is exactly one symbol error in the received words $(r = 1)$.

(2) According to the graph on the specification page, the vector ${\it \underline{\Lambda}}_l$ here has $L = n - k \ \underline{= 3}$ elements.

(3) There are only the two ELP coefficient vectors. ${\it \underline{\Lambda}}_1 = (\lambda_0, \, 1, \, 0)$ und ${\it \underline{\Lambda}}_2 = (0, \, \lambda_0, \, 1) \ \Rightarrow \ l_{\rm max} \ \underline{= 2}$.

(4) From ${\it \underline{\Lambda}}_1$ and ${\it \underline{\Lambda}}_2$ we get two scalar equations of determination ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for the parameter $\lambda_0$:

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

The system of equations is uniquely solvable ⇒ Answer YES.

(5) Using the result of subtask (4) ⇒ $\lambda_0 = \alpha$, we obtain for the error locator polynomial.

$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) =x \cdot \big (\alpha + x )$$

$$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Keine\hspace{0.15cm} Nullstelle}\hspace{0.05cm},$$

$$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Nullstelle}}\hspace{0.05cm}.$$

Verfälscht wurde also das Symbol an der Position 1 ⇒ Lösungsvorschlag 2.
Da die Berechnung in der Teilaufgabe (4) unter der Bedingung $r = 1$ erfolgte, wurden alle anderen Symbole richtig übertragen:

Umrechnungstabellen für das Galoisfeld $\rm GF(2^3)$

$$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$

(6) Aus der Bedingung $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}^{\rm T}$ folgt

$$(0, e_1, 0, 0, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12} \\ \alpha^5 & \alpha^{10} & \alpha^{15} \\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} \begin{pmatrix} \alpha^4\\ \alpha^5\\ \alpha^6 \end{pmatrix} $$

$$\Rightarrow \hspace{0.3cm} e_1 \cdot \alpha = \alpha^4\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$

Die Lösung führt stets zum Ergebnis $e_1 = \alpha^3$ ⇒ Antwort 2.
Mit dem Empfangswort $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$ erhält man das Decodierergebnis $\underline{z} = (\alpha^1, \, \alpha^3, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$.

(7) Analog zur Teilaufgabe (4) lautet nun das Gleichungssystem:

$$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

Die beiden Lösungen widersprechen sich. Bei der Übertragung sind mindestens zwei Symbole verfälscht worden. Die Decodierung versagt ⇒ Antwort NEIN.
Man müsste nun einen neuen Versuch gemäß dem roten Schema $(r = 2)$ starten.

	The blue highlighted schema $(r = 1)$.
	The red highlighted schema $(r = 2)$.
	The green highlighted schema $(r = 3)$.

	YES.
	NO.

	$e_i = \alpha^2$,
	$e_i = \alpha^3$,
	$e_i = 1$.

	YES.
	NO.