Aufgaben:Exercise 2.12Z: Reed-Solomon Syndrome Calculation

• Return to book

$\rm GF(2^3)$  representation as powers, polynomials, vectors

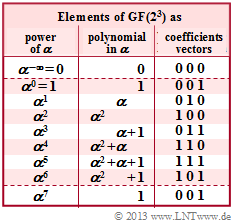
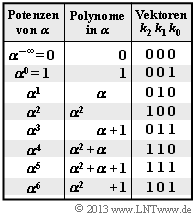
As in the  "Exercise 2. 12"  we consider the Reed–Solomon code  $(7, \, 4, \, 4)_8$  based on the Galois field  ${\rm GF}(q)$  with   $q = 8 = 2^3$.   The graph shows the corresponding conversion table.

Given are the possible code symbols in

1. exponent representation  $($powers of  $\alpha)$ 
2. polynomialrepresentation,
3. coefficient vector representation.

Given is the received word   $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$.

• Based on the syndrome   $\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$   it is to check whether individual symbols of the received vector  $\underline{y}$  were corrupted during transmission.

• Given is the parity-check matrix  $\mathbf{H}$  of the considered code and its transpose:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H}}^{\rm T} = \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

Hints:  This exercise refers to the section  "Step (A): Evaluation of the syndrome in BDD"  of the chapter  "Error Correction according to Reed–Solomon Coding".

Questions

1

It holds for the weceived word:   $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$. Specify the first element of the syndrome  $\underline{s} = (s_0, \, s_1, \, s_2)$.

	$s_0 = \alpha^4$,
	$s_0 = \alpha^5$,
	$s_0 = \alpha^6$,
	$s_0 = 0, \, 1, \, \alpha, \, \alpha^2$  or  $\alpha^3$.

2

What is the second syndrome element for the same received word?

	$s_1 = \alpha^4$,
	$s_1 = \alpha^5$,
	$s_1 = \alpha^6$,
	$s_1 = 0, \, 1, \, \alpha, \, \alpha^2$  or  $\alpha^3$.

3

What is the third syndrome element for the same received word?

	$s_2 = \alpha^4$,
	$s_2 = \alpha^5$,
	$s_2 = \alpha^6$,
	$s_2 = 0, \, 1, \, \alpha, \, \alpha^2$ oder $\alpha^3$.

4

Known is that the received word   $\underline{y}$   can be decoded correctly.  How many symbol errors does the received word contain?

$r \ = \ $

Solution

Solution

Conversion tables for the Galois field $\rm GF(2^3)$

(1)  The corresponding equation for syndrome calculation is:

$$\underline {s} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (s_0, s_1, s_2) = \begin{pmatrix} \alpha,0, \alpha^3,0, 1, \alpha,0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

The first element results in

$$s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^2 + 1 \cdot \alpha^4 + \alpha \cdot \alpha^5= \alpha + \alpha^5 + \alpha^4+ \alpha^6$$

$$\Rightarrow\hspace{0.3cm} s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\alpha) + (\alpha^2 + \alpha+ 1)+ (\alpha^2 + \alpha) + + (\alpha^2 + 1) = \alpha^2 + \alpha = \alpha^4\hspace{0.05cm}.$$

Correct is the proposed solution 1.

(2)  Correspondingly, for the second syndrome element, the proposed solution 2 applies accordingly:

$$s_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^4 + 1 \cdot \alpha^1 + \alpha \cdot \alpha^3= \alpha + \alpha^7 + \alpha+ \alpha^4= 1 + \alpha^4 = \alpha^2 + \alpha + 1 = \alpha^5 \hspace{0.05cm}.$$

(3)  To calculate $s_2$ must be multiplied by the last matrix column:

$$s_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^6 + 1 \cdot \alpha^5 + \alpha \cdot \alpha^1= \alpha + \alpha^2 + \alpha^5 + \alpha^2=\alpha^5 + \alpha = (\alpha^2 + \alpha + 1) + \alpha = \alpha^2 + 1 = \alpha^5 \hspace{0.05cm}.$$

Correct is the proposed solution 3.

(4)  Due to the calculated syndrome $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6) ≠ 0$ the received word contains at least one symbol error   ⇒   $r > 0$.

• The present Reed–Solomon–code $(7, \, 4, \, 4)_8 \ \Rightarrow \ d_{\rm min} = 4$ cannot correct more than $t = ⌊d_{\rm min}/2⌋ = 1$ errors.
• Since the received word can actually be decoded according to the specification,  $\underline{r = 1}$ holds.