Difference between revisions of "Aufgaben:Exercise 2.16: Bounded Distance Decoding: Decision Regions"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Error_Probability_and_Areas_of_Application}} |
| + | Betrachtete Codierraumschemata | ||
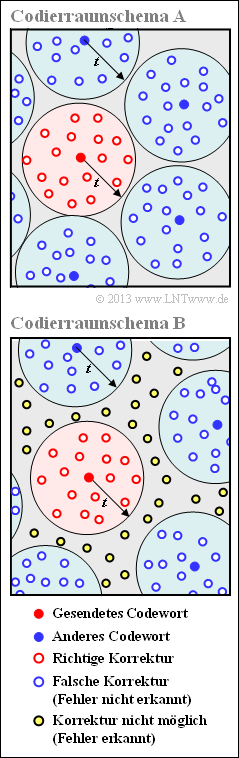
| + | [[File: P_ID2583__KC_A_2_16neu.png|right|frame|Considered coding space schemes]] | ||
| + | We assume a block code of length $n$ with symbols $c_i ∈ {\rm GF}(2^m)$ that can correct up to $t$ symbols. Each possible received word $\underline{y}_i$ can then be viewed as a point in a high-dimensional space. Assuming the basis ${\rm GF}(2) = \{0, \, 1\}$ the dimension $n is \cdot m$. | ||
| − | + | The diagram shows such a space in simplified, schematic two dimensional representation. | |
| − | |||
| − | + | The illustration is to be interpreted as follows: | |
| + | * The red dot $\underline{c}_j$ was sent. All red outlined points $\underline{y}_i$ in a hypersphere around this point $\underline{c}_j$ with the parameter $t$ as radius can be corrected. Using the nomenclature according to the [[Channel_Coding/Error_Probability_and_Areas_of_Application#Block_error_probability_for_RSC_and_BDD|"graph"]] in the theory section, then $\underline{z}_i = \underline{c}_j$ <br>⇒ "Error correction is successful". | ||
| − | + | * For very many symbol errors, $\underline{c}_j$ may be corrupted into a blue (or white-blue) dot $\underline{y}_j$ belonging to the hyper-sphere of another codeword $\underline{c}_{k ≠ j}$ . In this case the decoder makes a wrong decision <br>⇒ "The received word $\underline{y}_j$ is decoded incorrectly". | |
| − | * | ||
| − | * | + | * Finally, as in the sketch below, there may be yellow dots that do not belong to any hypersphere <br>⇒ "The received word $\underline{y}_j$ is not decodable". |
| − | |||
| + | In this exercise you are to decide which of the two code space schemes is suitable for describing | ||
| + | * [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|"Bounded Distance Decoding (BDD) of Hamming codes"]] respectively. | ||
| + | * [[Channel_Coding/Error_Probability_and_Areas_of_Application#Block_error_probability_for_RSC_and_BDD|"Bounded Distance Decoding (BDD) by Reed–Solomon codes"]]. | ||
| − | |||
| − | |||
| − | |||
| Line 24: | Line 25: | ||
| + | Hints: | ||
| + | * The exercise complements the topic of the chapter [[Channel_Coding/Error_Probability_and_Areas_of_Application|"Error Probability and Application Areas"]]. | ||
| + | * It is intended to illustrate significant differences in decoding Reed–Solomon codes and Hamming codes. | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Questions=== | |
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which coding space scheme applies to the Hamming codes? |
|type="()"} | |type="()"} | ||
| − | + | + | + Coding space scheme $\rm A$, |
| − | - | + | - Coding space scheme $\rm B$. |
| − | { | + | {Which statement is true for the probability that a received word $\underline{y}$ cannot be decoded when Hamming coding? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The probability ${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is exactly zero. |
| − | - ${\rm Pr}(\underline{y} \rm \ | + | - ${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is nonzero, but negligible. |
| − | - | + | - It holds ${\rm Pr}(\underline{y} {\rm \ is \ not \ decodable}) > {\rm Pr}(\underline{y} \rm \ is \ incorrectly \ decoded)$. |
| − | { | + | {Which coding space scheme applies to the Reed–Solomon codes? |
|type="()"} | |type="()"} | ||
| − | - | + | - Coding space scheme $\rm A$, |
| − | + | + | + Coding space scheme $\rm B$. |
| − | { | + | {Which statement applies to the probability that a received word $\underline{y}$ cannot be decoded after Reed–Solomon coding? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The probability ${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is exactly zero. |
| − | - ${\rm Pr}(\underline{y} \rm \ | + | - ${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is nonzero, but negligible. |
| − | + | + | + It holds ${\rm Pr}(\underline{y} {\rm \ is \ not \ decodable}) > {\rm Pr}(\underline{y} \rm \ is \ incorrectly \ decoded)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is <u>solution 1</u>, since the coding space scheme $\rm A$ describes a perfect code and each Hamming code $(n, \, k, \, 3)$ is a perfect code: |
| − | * | + | *For any Hamming code $(n, \, k, \, 3)$, there are a total of $2^n$ possible received words $\underline{y}_i$, which are assigned to one of $2^k$ possible codewords $\underline{c}_j$ during syndrome decoding. |
| − | * | + | *Because of the HC property $d_{\rm min} = 3$, all spheres in $n$ dimensional space have radius $t = 1$. Thus in all spheres there are $2^{n-k}$ points, for example. |
| − | :* $\text{HC (7, 4, 3)}$: | + | :* $\text{HC (7, 4, 3)}$: one point for error-free transmission and seven points for a bit error ⇒ $1 + 7 = 8 = 2^3 = 2^{7-4}$. |
| − | :* $\text{HC (15, 11, 3)}$: | + | :* $\text{HC (15, 11, 3)}$: one point for error-free transmission and now 15 points for a bit error ⇒ $1 + 15 = 16 = 2^4 = 2^{15-11}$. |
| − | + | Note: Since the Hamming code is a binary code, here the code space has the dimension $n$. | |
| − | '''(2)''' | + | '''(2)''' Correct is <u>answer 1</u>: |
| − | * | + | *In the gray area outside "spheres" there is not a single point in a perfect code. |
| − | * | + | *This was also shown in the calculation for subtask (1). |
| − | '''(3)''' | + | '''(3)''' The Reed–Solomon codes are described by the coding space scheme $\rm B$ ⇒ <u>Answer 2</u>. |
| − | * | + | *Here there are numerous yellow points in the gray area, i.e. points that cannot be assigned to any sphere in <i>Bounded Distance Decoding</i> (BDD). |
| − | * | + | *For example, if we consider the $\rm RSC \, (7, \, 3, \, 5)_8$ with code parameters $n = 7, \, k = 3$ and $t = 2$, there are a total of $8^7 = 2097152$ points and $8^3 = 512$ hypersphere here. |
| − | * | + | *If this code were perfect, then there should be $8^4 = 4096$ points within each sphere. However, it holds: |
:$${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} | :$${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} | ||
= {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 | = {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *For ${\rm Pr}(f = 1)$ it is considered that there can be "$7 \rm \ over \ 1$" $= 7$ error positions, and for each error position also seven different error values. The same is considered for ${\rm Pr}(f = 2)$. |
| − | '''(4)''' | + | '''(4)''' Correct is <u>answer 3</u>: |
| − | * | + | *A point in gray no-man's land is reached with fewer symbol errors than a point in another hypersphere. |
| − | * | + | *For long codes, an upper bound on the corruption probability is given in the literature: |
:$${\rm Pr}(\underline{y}_{i} {\rm \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} | :$${\rm Pr}(\underline{y}_{i} {\rm \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} | ||
Revision as of 18:19, 17 September 2022
Betrachtete Codierraumschemata
We assume a block code of length $n$ with symbols $c_i ∈ {\rm GF}(2^m)$ that can correct up to $t$ symbols. Each possible received word $\underline{y}_i$ can then be viewed as a point in a high-dimensional space. Assuming the basis ${\rm GF}(2) = \{0, \, 1\}$ the dimension $n is \cdot m$.
The diagram shows such a space in simplified, schematic two dimensional representation.
The illustration is to be interpreted as follows:
- The red dot $\underline{c}_j$ was sent. All red outlined points $\underline{y}_i$ in a hypersphere around this point $\underline{c}_j$ with the parameter $t$ as radius can be corrected. Using the nomenclature according to the "graph" in the theory section, then $\underline{z}_i = \underline{c}_j$
⇒ "Error correction is successful".
- For very many symbol errors, $\underline{c}_j$ may be corrupted into a blue (or white-blue) dot $\underline{y}_j$ belonging to the hyper-sphere of another codeword $\underline{c}_{k ≠ j}$ . In this case the decoder makes a wrong decision
⇒ "The received word $\underline{y}_j$ is decoded incorrectly".
- Finally, as in the sketch below, there may be yellow dots that do not belong to any hypersphere
⇒ "The received word $\underline{y}_j$ is not decodable".
In this exercise you are to decide which of the two code space schemes is suitable for describing
- "Bounded Distance Decoding (BDD) of Hamming codes" respectively.
- "Bounded Distance Decoding (BDD) by Reed–Solomon codes".
Hints:
- The exercise complements the topic of the chapter "Error Probability and Application Areas".
- It is intended to illustrate significant differences in decoding Reed–Solomon codes and Hamming codes.
Questions
Solution
- For any Hamming code $(n, \, k, \, 3)$, there are a total of $2^n$ possible received words $\underline{y}_i$, which are assigned to one of $2^k$ possible codewords $\underline{c}_j$ during syndrome decoding.
- Because of the HC property $d_{\rm min} = 3$, all spheres in $n$ dimensional space have radius $t = 1$. Thus in all spheres there are $2^{n-k}$ points, for example.
- $\text{HC (7, 4, 3)}$: one point for error-free transmission and seven points for a bit error ⇒ $1 + 7 = 8 = 2^3 = 2^{7-4}$.
- $\text{HC (15, 11, 3)}$: one point for error-free transmission and now 15 points for a bit error ⇒ $1 + 15 = 16 = 2^4 = 2^{15-11}$.
Note: Since the Hamming code is a binary code, here the code space has the dimension $n$.
(2) Correct is answer 1:
- In the gray area outside "spheres" there is not a single point in a perfect code.
- This was also shown in the calculation for subtask (1).
(3) The Reed–Solomon codes are described by the coding space scheme $\rm B$ ⇒ Answer 2.
- Here there are numerous yellow points in the gray area, i.e. points that cannot be assigned to any sphere in Bounded Distance Decoding (BDD).
- For example, if we consider the $\rm RSC \, (7, \, 3, \, 5)_8$ with code parameters $n = 7, \, k = 3$ and $t = 2$, there are a total of $8^7 = 2097152$ points and $8^3 = 512$ hypersphere here.
- If this code were perfect, then there should be $8^4 = 4096$ points within each sphere. However, it holds:
- $${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} = {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 \hspace{0.05cm}.$$
- For ${\rm Pr}(f = 1)$ it is considered that there can be "$7 \rm \ over \ 1$" $= 7$ error positions, and for each error position also seven different error values. The same is considered for ${\rm Pr}(f = 2)$.
(4) Correct is answer 3:
- A point in gray no-man's land is reached with fewer symbol errors than a point in another hypersphere.
- For long codes, an upper bound on the corruption probability is given in the literature:
- $${\rm Pr}(\underline{y}_{i} {\rm \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} = {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} \hspace{0.05cm}.$$
- Für den ${\rm RSC} \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$ liefert diese obere Schranke den Wert $1/(16!) < 10^{-14}$.