Difference between revisions of "Aufgaben:Exercise 2.2: Modulation Depth"
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Double-Sideband_Amplitude_Modulation |
}} | }} | ||
| − | [[File:P_ID989__Mod_A_2_2.png|right|frame| | + | [[File:P_ID989__Mod_A_2_2.png|right|frame|Definition of modulation depth for DSB–AM]] |
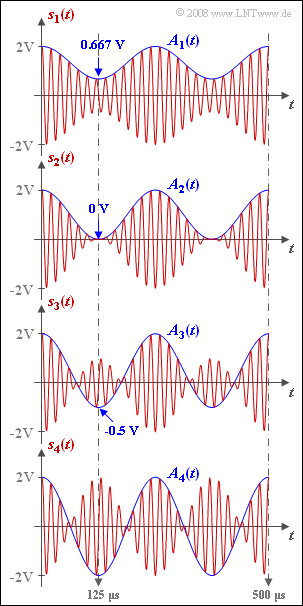
| − | + | The graph shows "DSB amplitude-modulated signals" $s_1(t)$ to $s_4(t)$ with differing modulation depth $m$. Let the message signal $q(t)$ and the carrier signal $z(t)$ each be cosine: | |
:$$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ | :$$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ | ||
:$$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ | :$$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| − | + | The modulated signal (transmitted signal) with the DC component added in the modulator is $A_{\rm T}$: | |
:$$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ | :$$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ | ||
| − | + | In the graphs, the chosen normalization was: | |
:$$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ | :$$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ | ||
| − | * | + | *If the modulation depth is $m ≤ 1$, then $A(t)= q(t) + A_{\rm T}$ is equal to the envelope $a(t)$. |
| − | * | + | *In contrast, for a modulation depth $m > 1$: |
:$$a(t ) = |A(t)|\hspace{0.05cm}.$$ | :$$a(t ) = |A(t)|\hspace{0.05cm}.$$ | ||
| + | *The cosine curve $A(t)$ varies between $A_{\rm max}$ and $A_{\rm min}$; because of normalization, ⇒ $A_{\rm max} = 2 \ \rm V$. | ||
| + | *The minimum values of $A(t)$ occur at half the period of the source signal $($i.e., for $t = 125 \ \rm µ s)$: | ||
| + | :$$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$ | ||
| + | *The numerical values are given in the graph. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | Hints: | |
| − | + | *This exercise belongs to the chapter [[Modulation_Methods/Double-Sideband_Amplitude_Modulation|Double-Sideband Amplitude Modulation]]. | |
| − | + | *Particular reference is made to the page [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Double-Sideband_Amplitude_Modulation_with_carrier|DSB-AM with carrier]]. | |
| + | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the modulation depth for each of the signals $s_1(t)$, $s_2(t)$, $s_3(t)$. |
|type="{}"} | |type="{}"} | ||
| − | $m_1$ | + | $m_1 \ = \ $ { 0.5 3% } |
| − | $m_2$ | + | $m_2 \ = \ $ { 1 3% } |
| − | $m_3$ | + | $m_3 \ = \ $ { 3 3% } |
| − | { | + | {Which statements are true for the signal $s_4(t)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + This is a case of "DSB–AM without carrier". |
| − | - | + | - The modulation depth is $m = 0$. |
| − | + | + | + The modulation depth $m$ is infinite. |
| − | { | + | {Let $A_{\rm T} = A_{\rm N} = 1\ \rm V$ ⇒ $m = 1$. What is the spectrum $S_+(f)$ of the analytical signal? Which Dirac weights occur at $f_{\rm T}$ as well as at $f_{\rm T}± f_{\rm N}$? |
|type="{}"} | |type="{}"} | ||
| − | $S_+( | + | $S_+(f_{\rm T}) \ = \ $ { 1 3% } $\ \text{V}$ |
| − | $S_+( | + | $S_+(f_{\rm T} ± f_{\rm N}) \ = \ $ { 0.5 3% } $\ \text{V}$ |
| − | { | + | {Now let $m = 1$. Which fraction $P_{\rm T}/P_{\rm S}$ of the total transmission power $P_{\rm S}$ is due to the carrier alone, and thus cannot be used for demodulation?? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $P_{\rm T}/P_{\rm S} \ = \ $ { 0.667 3% } |
| − | { | + | {Generalize the result from '''(4)''' for an arbitrary modulation depth $m$. What are the power ratios for $m = 0.5$, $m = 3$ and $m → ∞$? |
|type="{}"} | |type="{}"} | ||
| − | $m = 0.5 : | + | $m = 0.5\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $ { 0.889 3% } |
| − | $m = 3.0 | + | $m = 3.0\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $ { 0.182 3% } |
| − | $m → ∞ : | + | $m → ∞ \text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $ { 0. } |
| − | { | + | {Based on the calculations so far, which of the following statements seem reasonable to you? |
|type="[]"} | |type="[]"} | ||
| − | + m ≈ 1 | + | + $m ≈ 1$ is more favorable than a small $m$ for energy reasons. |
| − | + | + | + The carrier is only useful for envelope demodulation. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' From the two equations |
| − | $$ A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$ | + | :$$ A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$ |
| − | + | directly follows: | |
| − | $$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2 | + | :$$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2,\hspace{0.3cm} |
| − | + | A_{\rm T} = (A_{\rm max} + A_{\rm min})/2\hspace{0.05cm}.$$ | |
| − | + | *Thus, the modulation depth is | |
| − | $$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$ | + | :$$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$ |
| − | + | *With the given numerical values, one obtains: | |
| − | $$ m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm} | + | :$$ m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm}\underline {= 1.0}\hspace{0.05cm}, \hspace{0.5cm} |
| − | + | m_3 = \frac{2\,{\rm V} -(-1\,{\rm V})}{2\,{\rm V} + (-1\,{\rm V})} \hspace{0.15cm}\underline{=3.0}\hspace{0.05cm}.$$ | |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Answers 1 and 3</u> are correct: | ||
| + | *In this case, $A_{\rm T} = 0$, which means it is indeed "DSB-AM without carrier". | ||
| + | *The modulation depth $m = A_{\rm N}/A_{\rm T}$ is infinitely large. | ||
| + | |||
| + | |||
| + | |||
| + | [[File:P_ID990__Mod_A_2_2_c.png|right|frame|Analytical signal's spectrum ]] | ||
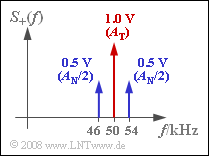
| + | '''(3)''' The spectrum $S_+(f)$ is composed of three Dirac delta lines for each modulation depth $m$ with the following weights: | ||
| + | *$A_{\rm T}$ $($at $f = f_{\rm T})$, | ||
| + | * $m/2 · A_{\rm T}$ $($at $f = f_{\rm T} ± f_{\rm N})$. | ||
| + | |||
| + | |||
| + | For $m = 1$, the weights are obtained according to the graph: | ||
| + | *$S_+(f_{\rm T}) = 1\ \rm V$, | ||
| + | *$S_+(f_{\rm T} ± f_{\rm T}) = 0.5\ \rm V$. | ||
| + | |||
| − | ''' | + | '''(4)''' The power (mean square) of a harmonic oscillation with amplitude $A_{\rm T} = 1 \ \rm V$ referenced to the $1 \ Ω$ resistor is: |
| + | :$$P_{\rm T} ={A_{\rm T}^2}/{2} = 0.5\,{\rm V}^2 \hspace{0.05cm}.$$ | ||
| + | *In the same way, for the powers of the lower and the upper sideband we obtain: | ||
| + | :$$P_{\rm LSB} = P_{\rm USB} =({A_{\rm N}}/{2})^2/2 = 0.125\,{\rm V}^2 \hspace{0.05cm}.$$ | ||
| + | *Thus, for $m=1$, the ratio we are looking for is: | ||
| + | :$${P_{\rm T}}/{P_{\rm S}}= \frac{P_{\rm T}}{P_{\rm USB} + P_{\rm T}+ P_{\rm OSB}}= \frac{0.5\,{\rm V}^2}{0.125\,{\rm V}^2 + 0.5\,{\rm V}^2+ 0.125\,{\rm V}^2}= 2/3\hspace{0.15cm}\underline { = 0.667}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | ''' | + | '''(5)''' Using the Dirac weights $m/2 · A_{\rm T}$ of the two sidebands corresponding to subtask '''(3)''', we get: |
| − | + | :$${P_{\rm T}}/{P_{\rm S}}= \frac{A_{\rm T}^2/2}{A_{\rm T}^2/2 + 2 \cdot (m/2)^2 \cdot A_{\rm T}^2/2}= \frac{2}{2 + m^2}\hspace{0.05cm}.$$ | |
| − | + | *This leads to the numerical values $8/9 = 0.889$ $($for $m = 0.5)$, $2/11 = 0.182$ $($for $m = 3)$, $0$ $($for $m \to ∞$). | |
| − | |||
| − | |||
| − | $$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' <u>Both statements</u> are true: | |
| + | *The addition of the carrier only makes sense in order to use the simpler envelope demodulator. This is only possible for $m \le 1$. | ||
| + | *However, should the modulation depth be $m > 1$ and the use of a synchronous demodulator therefore be required, the carrier should be (almost) completely omitted for energy reasons. | ||
| + | *Similarly due to energy concerns, if an envelope demodulator is used, the largest possible modulation depth $m < 1$ ⇒ $m \to 1$ should be aimed for. | ||
| + | *However, a small residual carrier can facilitate carrier recovery, which is needed in a synchronous demodulator for frequency and phase synchronization. Thus, the second statement is only conditionally correct. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.1 Double Sideband Amplitude Modulation^]] |
Latest revision as of 16:17, 18 January 2023
The graph shows "DSB amplitude-modulated signals" $s_1(t)$ to $s_4(t)$ with differing modulation depth $m$. Let the message signal $q(t)$ and the carrier signal $z(t)$ each be cosine:
- $$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$
- $$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$
The modulated signal (transmitted signal) with the DC component added in the modulator is $A_{\rm T}$:
- $$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$
In the graphs, the chosen normalization was:
- $$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$
- If the modulation depth is $m ≤ 1$, then $A(t)= q(t) + A_{\rm T}$ is equal to the envelope $a(t)$.
- In contrast, for a modulation depth $m > 1$:
- $$a(t ) = |A(t)|\hspace{0.05cm}.$$
- The cosine curve $A(t)$ varies between $A_{\rm max}$ and $A_{\rm min}$; because of normalization, ⇒ $A_{\rm max} = 2 \ \rm V$.
- The minimum values of $A(t)$ occur at half the period of the source signal $($i.e., for $t = 125 \ \rm µ s)$:
- $$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$
- The numerical values are given in the graph.
Hints:
- This exercise belongs to the chapter Double-Sideband Amplitude Modulation.
- Particular reference is made to the page DSB-AM with carrier.
Questions
Solution
- $$ A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$
directly follows:
- $$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2,\hspace{0.3cm} A_{\rm T} = (A_{\rm max} + A_{\rm min})/2\hspace{0.05cm}.$$
- Thus, the modulation depth is
- $$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$
- With the given numerical values, one obtains:
- $$ m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm}\underline {= 1.0}\hspace{0.05cm}, \hspace{0.5cm} m_3 = \frac{2\,{\rm V} -(-1\,{\rm V})}{2\,{\rm V} + (-1\,{\rm V})} \hspace{0.15cm}\underline{=3.0}\hspace{0.05cm}.$$
(2) Answers 1 and 3 are correct:
- In this case, $A_{\rm T} = 0$, which means it is indeed "DSB-AM without carrier".
- The modulation depth $m = A_{\rm N}/A_{\rm T}$ is infinitely large.
(3) The spectrum $S_+(f)$ is composed of three Dirac delta lines for each modulation depth $m$ with the following weights:
- $A_{\rm T}$ $($at $f = f_{\rm T})$,
- $m/2 · A_{\rm T}$ $($at $f = f_{\rm T} ± f_{\rm N})$.
For $m = 1$, the weights are obtained according to the graph:
- $S_+(f_{\rm T}) = 1\ \rm V$,
- $S_+(f_{\rm T} ± f_{\rm T}) = 0.5\ \rm V$.
(4) The power (mean square) of a harmonic oscillation with amplitude $A_{\rm T} = 1 \ \rm V$ referenced to the $1 \ Ω$ resistor is:
- $$P_{\rm T} ={A_{\rm T}^2}/{2} = 0.5\,{\rm V}^2 \hspace{0.05cm}.$$
- In the same way, for the powers of the lower and the upper sideband we obtain:
- $$P_{\rm LSB} = P_{\rm USB} =({A_{\rm N}}/{2})^2/2 = 0.125\,{\rm V}^2 \hspace{0.05cm}.$$
- Thus, for $m=1$, the ratio we are looking for is:
- $${P_{\rm T}}/{P_{\rm S}}= \frac{P_{\rm T}}{P_{\rm USB} + P_{\rm T}+ P_{\rm OSB}}= \frac{0.5\,{\rm V}^2}{0.125\,{\rm V}^2 + 0.5\,{\rm V}^2+ 0.125\,{\rm V}^2}= 2/3\hspace{0.15cm}\underline { = 0.667}\hspace{0.05cm}.$$
(5) Using the Dirac weights $m/2 · A_{\rm T}$ of the two sidebands corresponding to subtask (3), we get:
- $${P_{\rm T}}/{P_{\rm S}}= \frac{A_{\rm T}^2/2}{A_{\rm T}^2/2 + 2 \cdot (m/2)^2 \cdot A_{\rm T}^2/2}= \frac{2}{2 + m^2}\hspace{0.05cm}.$$
- This leads to the numerical values $8/9 = 0.889$ $($for $m = 0.5)$, $2/11 = 0.182$ $($for $m = 3)$, $0$ $($for $m \to ∞$).
(6) Both statements are true:
- The addition of the carrier only makes sense in order to use the simpler envelope demodulator. This is only possible for $m \le 1$.
- However, should the modulation depth be $m > 1$ and the use of a synchronous demodulator therefore be required, the carrier should be (almost) completely omitted for energy reasons.
- Similarly due to energy concerns, if an envelope demodulator is used, the largest possible modulation depth $m < 1$ ⇒ $m \to 1$ should be aimed for.
- However, a small residual carrier can facilitate carrier recovery, which is needed in a synchronous demodulator for frequency and phase synchronization. Thus, the second statement is only conditionally correct.