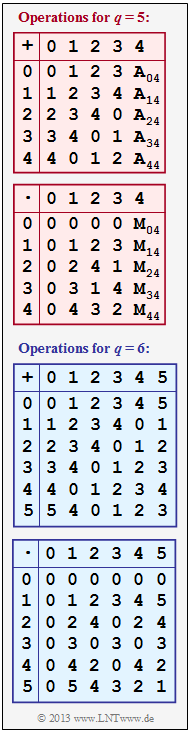
Difference between revisions of "Aufgaben:Exercise 2.2: Properties of Galois Fields"

From LNTwww
Line 1: Line 1:
−
{{quiz-Header|Buchseite=Kanalcodierung/Einige Grundlagen der Algebra}}
+
{{quiz-Header|Buchseite=Channel_Coding/Some_Basics_of_Algebra}}
  
−
[[File:EN_KC_A_2_2.png|right|frame|Addition / Multiplikation für  $q = 5$  und  $q = 6$]]
+
[[File:EN_KC_A_2_2.png|right|frame|Addition / multiplication for  $q = 5$  and  $q = 6$]]
−
Wir betrachten hier die Zahlenmengen
+
Here we consider the sets of numbers
 
* $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
 
* $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
 
* $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
 
* $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
  
  
−
In nebenstehender Grafik sind die (teilweise unvollständigen) Additions– und Multiplikationstabellen für  $q = 5$  und  $q = 6$  angegeben, wobei sowohl die Addition  ("$+$")  als auch die Multiplikation  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  zu verstehen sind.
+
In the adjacent graph, the (partially incomplete) addition– and multiplication tables for  $q = 5$  and  $q = 6$  are given, where both addition  ("$+$")  and multiplication  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  are to be understood.
  
−
Zu überprüfen ist, ob die Zahlenmengen  $Z_5$  und  $Z_6$  alle Bedingungen eines Galoisfeldes  $\rm GF(5)$  bzw.  $\rm GF(6)$  erfüllen.  
+
To be checked is whether the sets of numbers  $Z_5$  and  $Z_6$  satisfy all the conditions of a Galois field  $\rm GF(5)$  and  $\rm GF(6)$  respectively.  
  
−
Im  [[Channel_Coding/Einige_Grundlagen_der_Algebra#Definition_eines_Galoisfeldes|Theorieteil]]  werden insgesamt acht Bedingungen genannt, die alle erfüllt sein müssen. Sie sollen nur zwei dieser Bedingungen überprüfen:
+
In the  [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"theory section"]]  a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:
  
−
$\rm(D)$&nbsp;  Für alle Elemente gibt es eine&nbsp; <b>additive Inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$+$"</i>):
+
$\rm(D)$&nbsp;  For all elements there is an&nbsp; <b>additive inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$+$"</i>):
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0  \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0  \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
{\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
 
{\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
  
−
$\rm(E)$&nbsp;  Alle Elemente haben eine&nbsp; <b>multiplikative Inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"</i>):
+
$\rm(E)$&nbsp;  All elements have a <b>multiplicative inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"</i>):
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
{\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
 
{\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
  
−
Die weiteren Bedingungen für ein Galoisfeld, nämlich
+
The other conditions for a Galois field, viz.
 
* Closure,  
 
* Closure,  
−
* Existenz von Null&ndash; und Einselelement,
+
* Existence of zero&ndash; and identity element,
−
* Gültigkeit von Kommutativ&ndash;, Assoziativ&ndash; und Distributivgesetz
+
* validity of commutative&ndash;, associative&ndash; and distributive law
  
  
−
werden sowohl von $Z_5$ als auch von $Z_6$ erfüllt.
+
are satisfied by both $Z_5$ and $Z_6$.
  
  
Line 35: Line 35:
  
  
−
''Hinweis:''
+
Hints:
−
* Die Aufgabe bezieht sich auf das Kapitel&nbsp; [[Channel_Coding/Einige_Grundlagen_der_Algebra| Einige Grundlagen der Algebra]].
+
* The exercise refers to the chapter&nbsp; [[Channel_Coding/Some_Basics_of_Algebra| Some Basics of Algebra]].
  
  
  
  
−
===Fragebogen===
+
===Questions===
 
<quiz display=simple>
 
<quiz display=simple>
−
{Ergänzen Sie die Additionstabelle für&nbsp; $q = 5$. Geben Sie folgende Werte ein:
+
{Complete the addition table for&nbsp; $q = 5$. Enter the following values:
 
|type="{}"}
 
|type="{}"}
 
$A_{04} \ = \ ${ 4 }
 
$A_{04} \ = \ ${ 4 }
Line 49: Line 49:
 
$A_{44} \ = \ ${ 3 }
 
$A_{44} \ = \ ${ 3 }
  
−
{Ergänzen Sie die Multiplikationstabelle für&nbsp; $q = 5$. Geben Sie folgende Werte ein:
+
{Complete the multiplication table for&nbsp; $q = 5$. Enter the following values:
 
|type="{}"}
 
|type="{}"}
 
$M_{04} \ = \ ${ 0. }
 
$M_{04} \ = \ ${ 0. }
Line 55: Line 55:
 
$M_{44} \ = \ ${ 1. }
 
$M_{44} \ = \ ${ 1. }
  
−
{Erfüllt die Menge&nbsp; $Z_5$&nbsp; die Bedingungen eines Galoisfeldes?
+
{Does the set&nbsp; $Z_5$&nbsp; satisfy the conditions of a Galois field?
 
|type="[]"}
 
|type="[]"}
−
+ Ja.
+
+ Yes.
−
- Nein, es gibt nicht für alle Elemente&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$&nbsp; eine additive Inverse.
+
- No, there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$&nbsp;.
−
- Nein, die Elemente&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$&nbsp; haben nicht alle eine multiplikative Inverse.
+
- No, the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$&nbsp; do not all have a multiplicative inverse.
  
−
{Erfüllt die Menge&nbsp; $Z_6$&nbsp; die Bedingungen eines Galoisfeldes?
+
{Does the set&nbsp; $Z_6$&nbsp; satisfy the conditions of a Galois field?
 
|type="[]"}
 
|type="[]"}
−
- Ja.  
+
- Yes.  
−
- Nein, es gibt nicht für alle Elemente&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$&nbsp; eine additive Inverse.
+
- No, there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$&nbsp;.
−
+ Nein, die Elemente&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$&nbsp; haben nicht alle eine multiplikative Inverse.
+
+ No, the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$&nbsp; do not all have a multiplicative inverse.
  
−
{Die Zahlenmengen&nbsp; $Z_2, \ Z_3, \ Z_5$&nbsp; und $Z_7$&nbsp; ergeben ein Galoisfeld, die Mengen&nbsp; $Z_4, \ Z_6, \ Z_8, \ Z_9$&nbsp; dagegen nicht. Was folgern Sie daraus?
+
{The sets of numbers&nbsp; $Z_2, \ Z_3, \ Z_5$&nbsp; and $Z_7$&nbsp; yield a Galois field, but the sets&nbsp; $Z_4, \ Z_6, \ Z_8, \ Z_9$&nbsp; do not. What do you conclude from this?
 
|type="[]"}
 
|type="[]"}
−
- $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ ist ein Galoisfeld?
+
- $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
−
+ $Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ ist ein Galoisfeld?
+
+ $Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ is a Galois field?
−
- $Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ ist ein Galoisfeld?
+
- $Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ is a Galois field?
 
</quiz>
 
</quiz>
  

Revision as of 00:49, 26 August 2022

Addition / multiplication for  $q = 5$  and  $q = 6$

Here we consider the sets of numbers

  • $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
  • $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.


In the adjacent graph, the (partially incomplete) addition– and multiplication tables for  $q = 5$  and  $q = 6$  are given, where both addition  ("$+$")  and multiplication  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  are to be understood.

To be checked is whether the sets of numbers  $Z_5$  and  $Z_6$  satisfy all the conditions of a Galois field  $\rm GF(5)$  and  $\rm GF(6)$  respectively.

In the  "theory section"  a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:

$\rm(D)$  For all elements there is an  additive inverse  (Inverse  for  "$+$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$

$\rm(E)$  All elements have a multiplicative inverse  (Inverse  for  "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$

The other conditions for a Galois field, viz.

  • Closure,
  • Existence of zero– and identity element,
  • validity of commutative–, associative– and distributive law


are satisfied by both $Z_5$ and $Z_6$.




Hints:



Questions

1

Complete the addition table for  $q = 5$. Enter the following values:

$A_{04} \ = \ $
$A_{14} \ = \ $
$A_{44} \ = \ $

2

Complete the multiplication table for  $q = 5$. Enter the following values:

$M_{04} \ = \ $
$M_{14} \ = \ $
$M_{44} \ = \ $

3

Does the set  $Z_5$  satisfy the conditions of a Galois field?

Yes.
No, there is not an additive inverse for all elements  $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ .
No, the elements  $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$  do not all have a multiplicative inverse.

4

Does the set  $Z_6$  satisfy the conditions of a Galois field?

Yes.
No, there is not an additive inverse for all elements  $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ .
No, the elements  $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$  do not all have a multiplicative inverse.

5

The sets of numbers  $Z_2, \ Z_3, \ Z_5$  and $Z_7$  yield a Galois field, but the sets  $Z_4, \ Z_6, \ Z_8, \ Z_9$  do not. What do you conclude from this?

$Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
$Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ is a Galois field?
$Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ is a Galois field?


Musterlösung

Solution

(1)  Allgemein gilt für $0 ≤ \mu ≤ 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$. Daraus folgt:

$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$

Aufgrund des Kommutativgesetzes der Addition,

$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm f\ddot{u}r \hspace{0.2cm}alle\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$

ist natürlich die letzte Spalte der Additionstabelle identisch mit der letzten Zeile der gleichen Tabelle.


(2)  Nun gilt $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ und man erhält:

$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

Da die Multiplikation ebenfalls kommutativ ist, stimmt auch in der Multiplikationstabelle die letzte Spalte wieder mit der letzten Zeile überein.


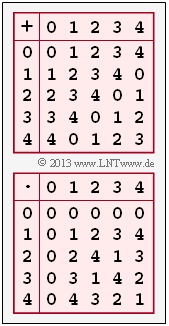
Tabellen zur Addition und Multiplikation für $q = 5$

(3)  Die Grafik zeigt die vollständigen Additions– und Multiplikationstabellen für $q = 5$. Man erkennt:

  • In der Additionstabelle gibt es in jeder Zeile (und auch in jeder Spalte) genau eine Null. Zu jedem $z_i ∈ Z_5$ gibt es also ein ${\rm Inv}_{\rm A} (z_i)$, das die Bedingung $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$ erfüllt:
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
  • In der Multiplikationstabelle lassen wir das Nullelement (erste Zeile und erste Spalte) außer Betracht. In allen anderen Zeilen und Spalten der unteren Tabelle gibt es tatsächlich jeweils genau eine Eins. Aus der Bedingung $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ erhält man:
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$

Da sowohl die erforderlichen additiven als auch die multiplikativen Inversen existieren beschreibt $Z_5$ ein Galoisfeld $\rm GF(5)$  

⇒  Richtig ist der Lösungsvorschlag 1.


(4)  Aus der blauen Additionstabelle auf der Angabenseite erkennt man, dass alle Zahlen $0, \, 1, \, 2, \, 3, \, 4, \, 5$ der Menge $Z_6$ eine additive Inverse besitzen  ⇒  in jeder Zeile (und Spalte) gibt es genau eine Null.

Eine multiplikative Inverse ${\rm Inv}_{\rm M}(z_i)$ gibt es dagegen nur für $z_i = 1$ und $z_i = 5$, nämlich

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$

Für $z_i = 2, \ z_i = 3$ und $z_i = 4$ findet man dagegen kein Element $z_j$, so dass $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$ ergibt.

Richtig ist also der Lösungsvorschlag 3   ⇒   Die blauen Tabellen für $q = 6$ ergeben kein Galoisfeld $\rm GF(6)$.


(5)  Richtig ist der Lösungsvorschlag 2:

  • Eine endliche Zahlenmenge $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ natürlicher Zahlen führt nur dann zu einem "endlichen Zahlenkörper" (dies ist die deutsche Bezeichnung für ein Galoisfeld), wenn $q$ eine Primzahl ist.
  • Von den oben genannten Zahlenmengen trifft dies nur auf $Z_{11}$ zu.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_2.2:_Properties_of_Galois_Fields&oldid=48560"
  • Powered by MediaWiki