Difference between revisions of "Aufgaben:Exercise 2.2: Properties of Galois Fields"

From LNTwww
 
(3 intermediate revisions by 2 users not shown)
Line 4: Line 4:
 
Here we consider the sets of numbers
 
Here we consider the sets of numbers
 
* $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
 
* $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
 +
 
* $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
 
* $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
  
  
−
In the adjacent graph, the (partially incomplete) addition– and multiplication tables for  $q = 5$  and  $q = 6$  are given, where both addition  ("$+$")  and multiplication  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  are to be understood.
+
In the adjacent graph,   the (partially incomplete)  addition and multiplication tables for  $q = 5$  and  $q = 6$  are given,  where both addition  ("$+$")  and multiplication  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  are to be understood.
  
−
To be checked is whether the sets of numbers  $Z_5$  and  $Z_6$  satisfy all the conditions of a Galois field  $\rm GF(5)$  and  $\rm GF(6)$  respectively.  
+
To be checked is whether the number sets  $Z_5$  and  $Z_6$  satisfy all the conditions of a Galois field  $\rm GF(5)$  and  $\rm GF(6)$,  respectively.  
  
−
In the  [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"theory section"]]  a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:
+
In the  [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"theory section"]]  a total of eight conditions are mentioned,  all of which must be met.  You are to check only two of these conditions:
  
−
$\rm(D)$&nbsp;  For all elements there is an&nbsp; <b>additive inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$+$"</i>):
+
$\rm(D)$&nbsp;  For all elements there is an&nbsp; <b>additive inverse</b>&nbsp; (Inverse&nbsp; for&nbsp; "$+$"):
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0  \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0  \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
{\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
 
{\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
  
−
$\rm(E)$&nbsp;  All elements have a <b>multiplicative inverse</b>&nbsp; (<i>Inverse&nbsp; for&nbsp; "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"</i>):
+
$\rm(E)$&nbsp;  All elements have a&nbsp; <b>multiplicative inverse</b>&nbsp; (Inverse&nbsp; for&nbsp; "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
:$$\forall \hspace{0.15cm}  z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}
 
{\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
 
{\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
Line 24: Line 25:
 
* Closure,  
 
* Closure,  
 
* Existence of zero&ndash; and identity element,
 
* Existence of zero&ndash; and identity element,
−
* validity of commutative&ndash;, associative&ndash; and distributive law
+
* validity of commutative law, associative law and distributive law
−
 
 
−
 
 
−
are satisfied by both $Z_5$ and $Z_6$.
 
  
  
 +
are satisfied by both,&nbsp; $Z_5$&nbsp; and&nbsp; $Z_6$.
  
  
Line 35: Line 34:
  
  
−
Hints:
+
Hints:&nbsp; The exercise refers to the chapter&nbsp; [[Channel_Coding/Some_Basics_of_Algebra| "Some Basics of Algebra"]].
−
* The exercise refers to the chapter&nbsp; [[Channel_Coding/Some_Basics_of_Algebra| Some Basics of Algebra]].
 
  
  
Line 43: Line 41:
 
===Questions===
 
===Questions===
 
<quiz display=simple>
 
<quiz display=simple>
−
{Complete the addition table for&nbsp; $q = 5$. Enter the following values:
+
{Complete the addition table for&nbsp; $q = 5$.&nbsp; Enter the following values:
 
|type="{}"}
 
|type="{}"}
 
$A_{04} \ = \ ${ 4 }
 
$A_{04} \ = \ ${ 4 }
Line 49: Line 47:
 
$A_{44} \ = \ ${ 3 }
 
$A_{44} \ = \ ${ 3 }
  
−
{Complete the multiplication table for&nbsp; $q = 5$. Enter the following values:
+
{Complete the multiplication table for&nbsp; $q = 5$.&nbsp; Enter the following values:
 
|type="{}"}
 
|type="{}"}
 
$M_{04} \ = \ ${ 0. }
 
$M_{04} \ = \ ${ 0. }
Line 55: Line 53:
 
$M_{44} \ = \ ${ 1. }
 
$M_{44} \ = \ ${ 1. }
  
−
{Does the set&nbsp; $Z_5$&nbsp; satisfy the conditions of a Galois field?
+
{Does the&nbsp; $Z_5$&nbsp; set satisfy the conditions of a Galois field?
 
|type="[]"}
 
|type="[]"}
 
+ Yes.
 
+ Yes.
−
- No, there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$&nbsp;.
+
- No,&nbsp; there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$&nbsp;.
−
- No, the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$&nbsp; do not all have a multiplicative inverse.
+
- No,&nbsp; the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$&nbsp; do not all have a multiplicative inverse.
  
−
{Does the set&nbsp; $Z_6$&nbsp; satisfy the conditions of a Galois field?
+
{Does the&nbsp; $Z_6$&nbsp; set satisfy the conditions of a Galois field?
 
|type="[]"}
 
|type="[]"}
 
- Yes.  
 
- Yes.  
−
- No, there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$&nbsp;.
+
- No,&nbsp; there is not an additive inverse for all elements&nbsp; $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$&nbsp;.
−
+ No, the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$&nbsp; do not all have a multiplicative inverse.
+
+ No,&nbsp; the elements&nbsp; $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$&nbsp; do not all have a multiplicative inverse.
  
−
{The sets of numbers&nbsp; $Z_2, \ Z_3, \ Z_5$&nbsp; and $Z_7$&nbsp; yield a Galois field, but the sets&nbsp; $Z_4, \ Z_6, \ Z_8, \ Z_9$&nbsp; do not. What do you conclude from this?
+
{The number sets&nbsp; $Z_2, \ Z_3, \ Z_5$&nbsp; and $Z_7$&nbsp; yield a Galois field,&nbsp; but the sets&nbsp; $Z_4, \ Z_6, \ Z_8, \ Z_9$&nbsp; do not.&nbsp; What do you conclude from this?
 
|type="[]"}
 
|type="[]"}
 
- $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
 
- $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
Line 74: Line 72:
 
</quiz>
 
</quiz>
  
−
===Musterlösung===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''(1)'''&nbsp; Allgemein gilt für $0 &#8804; \mu &#8804; 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$. Daraus folgt:
+
'''(1)'''&nbsp; In general,&nbsp; for&nbsp; $0 &#8804; \mu &#8804; 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$.&nbsp; It follows:
 
:$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
 
:$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
 
:$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
 
:$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
  
−
Aufgrund des Kommutativgesetzes der Addition,
+
Due to the commutative law of addition,
−
:$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm f\ddot{u}r \hspace{0.2cm}alle\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$
+
:$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm for \hspace{0.2cm}all\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$
  
−
ist natürlich die letzte Spalte der Additionstabelle identisch mit der letzten Zeile der gleichen Tabelle.
+
the last column of the addition table is of course identical to the last row of the same table.
  
  
  
−
'''(2)'''&nbsp; Nun gilt $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ und man erhält:
+
'''(2)'''&nbsp; Now $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$&nbsp; and we obtain:
 
:$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
 
:$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
 
:$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
 
:$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
  
−
Da die Multiplikation ebenfalls kommutativ ist, stimmt auch in der Multiplikationstabelle die letzte Spalte wieder mit der letzten Zeile überein.
+
Since multiplication is also commutative,&nbsp; the last column in the multiplication table again matches the last row.
 +
 
 +
 
  
 +
[[File:P_ID2493__KC_A_2_2c.png|right|frame|Addition/multiplication tables for&nbsp; $q = 5$]]
  
 +
'''(3)'''&nbsp; The graph shows the full addition and multiplication tables for&nbsp; $q = 5$.&nbsp; You can see:
 +
* In the addition table there is exactly one zero in each row&nbsp; (and also in each column).&nbsp;
  
−
[[File:P_ID2493__KC_A_2_2c.png|right|frame|Tabellen zur Addition und Multiplikation für $q = 5$]]
+
*So for every&nbsp; $z_i &#8712; Z_5$&nbsp; there is an&nbsp; ${\rm Inv}_{\rm A} (z_i)$&nbsp; that satisfies the condition&nbsp; $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$:
−
'''(3)'''&nbsp; Die Grafik zeigt die vollständigen Additions&ndash; und Multiplikationstabellen für $q = 5$. Man erkennt:
 
−
* In der Additionstabelle gibt es in jeder Zeile (und auch in jeder Spalte) genau eine Null. Zu jedem $z_i &#8712; Z_5$ gibt es also ein ${\rm Inv}_{\rm A} (z_i)$, das die Bedingung $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$ erfüllt:
 
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0  \hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0  \hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
Line 104: Line 105:
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
  
−
* In der Multiplikationstabelle lassen wir das Nullelement (erste Zeile und erste Spalte) außer Betracht. In allen anderen Zeilen und Spalten der unteren Tabelle gibt es tatsächlich jeweils genau eine Eins. Aus der Bedingung $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ erhält man:
+
* In the multiplication table we leave the zero element&nbsp; (first row and first column)&nbsp; out of consideration.  
 +
 
 +
*In all other rows and columns of the lower table there is indeed exactly one each.&nbsp;
 +
 
 +
*From the condition $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$&nbsp; one obtains:
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  1\hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  1\hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
Line 110: Line 115:
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
  
−
Da sowohl die erforderlichen additiven als auch die multiplikativen Inversen existieren beschreibt $Z_5$ ein Galoisfeld $\rm GF(5)$ &nbsp;
+
*Since both the required additive and multiplicative inverses exist &nbsp; &rArr; &nbsp; $Z_5$ describes a Galois field $\rm GF(5)$ &nbsp;
 +
 
 +
*Correct is the <u>proposed solution 1</u>.
  
−
&#8658;&nbsp; Richtig ist der <u>Lösungsvorschlag 1</u>.
 
  
  
 +
'''(4)'''&nbsp; From the blue addition table on the statement page,&nbsp; we see that all numbers&nbsp; $(0, \, 1, \, 2, \, 3, \, 4, \, 5)$&nbsp; of the set $Z_6$&nbsp; have an additive inverse
  
−
'''(4)'''&nbsp; Aus der blauen Additionstabelle auf der Angabenseite erkennt man, dass alle Zahlen $0, \, 1, \, 2, \, 3, \, 4, \, 5$ der Menge $Z_6$ eine additive Inverse besitzen &nbsp;&#8658;&nbsp; in jeder Zeile (und Spalte) gibt es genau eine Null.
+
&nbsp; &#8658; &nbsp; in each row&nbsp; (and column)&nbsp; there is exactly one zero.
  
−
Eine multiplikative Inverse ${\rm Inv}_{\rm M}(z_i)$ gibt es dagegen nur für $z_i = 1$ und $z_i = 5$, nämlich
+
*On the other hand,&nbsp; a multiplicative inverse&nbsp; ${\rm Inv}_{\rm M}(z_i)$&nbsp; exists only for&nbsp; $z_i = 1$&nbsp; and&nbsp; $z_i = 5$,&nbsp; viz.
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  1\hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  1\hspace{0.05cm},$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$
 
:$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5  \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}  z_i \cdot {\rm Inv_M}(z_i) =  25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$
  
−
Für $z_i = 2, \ z_i = 3$ und $z_i = 4$ findet man dagegen kein Element $z_j$, so dass $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$ ergibt.  
+
*For&nbsp; $z_i = 2, \ z_i = 3$ and $z_i = 4$,&nbsp; we find no element&nbsp; $z_j$,&nbsp; so that&nbsp; $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$.  
  
−
Richtig ist also der <u>Lösungsvorschlag 3</u> &nbsp; &rArr; &nbsp; Die blauen Tabellen für $q = 6$ ergeben kein Galoisfeld $\rm GF(6)$.
+
*Correct is the <u>proposed solution 3</u> &nbsp; &rArr; &nbsp; the blue tables for&nbsp; $q = 6$&nbsp; do not yield a Galois field&nbsp; $\rm GF(6)$.
  
  
  
−
'''(5)'''&nbsp; Richtig ist der <u>Lösungsvorschlag 2</u>:
+
'''(5)'''&nbsp; Correct is the&nbsp; <u>proposed solution 2</u>:
−
*Eine endliche Zahlenmenge $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ natürlicher Zahlen führt nur dann zu einem "endlichen Zahlenkörper" (dies ist die deutsche Bezeichnung für ein Galoisfeld), wenn $q$ eine Primzahl ist.  
+
*A finite number set&nbsp; $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$&nbsp; of natural numbers leads to a Galois field only if&nbsp; $q$&nbsp; is a prime number.
−
*Von den oben genannten Zahlenmengen trifft dies nur auf $Z_{11}$ zu.
+
 +
*Of the number sets mentioned above,&nbsp; this is true only for&nbsp; $Z_{11}$.
 
{{ML-Fuß}}
 
{{ML-Fuß}}
  
  
 
[[Category:Channel Coding: Exercises|^2.1 Some Basics of Algebra^]]
 
[[Category:Channel Coding: Exercises|^2.1 Some Basics of Algebra^]]

Latest revision as of 15:11, 28 August 2022

Addition / multiplication for  $q = 5$  and  $q = 6$

Here we consider the sets of numbers

  • $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
  • $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.


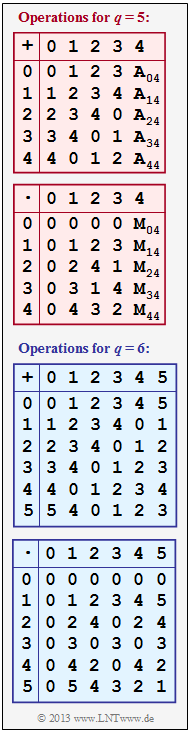
In the adjacent graph,  the (partially incomplete)  addition and multiplication tables for  $q = 5$  and  $q = 6$  are given,  where both addition  ("$+$")  and multiplication  ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$")  modulo  $q$  are to be understood.

To be checked is whether the number sets  $Z_5$  and  $Z_6$  satisfy all the conditions of a Galois field  $\rm GF(5)$  and  $\rm GF(6)$,  respectively.

In the  "theory section"  a total of eight conditions are mentioned,  all of which must be met.  You are to check only two of these conditions:

$\rm(D)$  For all elements there is an  additive inverse  (Inverse  for  "$+$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$

$\rm(E)$  All elements have a  multiplicative inverse  (Inverse  for  "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$

The other conditions for a Galois field, viz.

  • Closure,
  • Existence of zero– and identity element,
  • validity of commutative law, associative law and distributive law


are satisfied by both,  $Z_5$  and  $Z_6$.



Hints:  The exercise refers to the chapter  "Some Basics of Algebra".



Questions

1

Complete the addition table for  $q = 5$.  Enter the following values:

$A_{04} \ = \ $
$A_{14} \ = \ $
$A_{44} \ = \ $

2

Complete the multiplication table for  $q = 5$.  Enter the following values:

$M_{04} \ = \ $
$M_{14} \ = \ $
$M_{44} \ = \ $

3

Does the  $Z_5$  set satisfy the conditions of a Galois field?

Yes.
No,  there is not an additive inverse for all elements  $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ .
No,  the elements  $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$  do not all have a multiplicative inverse.

4

Does the  $Z_6$  set satisfy the conditions of a Galois field?

Yes.
No,  there is not an additive inverse for all elements  $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ .
No,  the elements  $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$  do not all have a multiplicative inverse.

5

The number sets  $Z_2, \ Z_3, \ Z_5$  and $Z_7$  yield a Galois field,  but the sets  $Z_4, \ Z_6, \ Z_8, \ Z_9$  do not.  What do you conclude from this?

$Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
$Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ is a Galois field?
$Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ is a Galois field?


Solution

Solution

(1)  In general,  for  $0 ≤ \mu ≤ 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$.  It follows:

$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$

Due to the commutative law of addition,

$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm for \hspace{0.2cm}all\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$

the last column of the addition table is of course identical to the last row of the same table.


(2)  Now $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$  and we obtain:

$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

Since multiplication is also commutative,  the last column in the multiplication table again matches the last row.


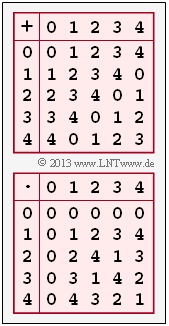
Addition/multiplication tables for  $q = 5$

(3)  The graph shows the full addition and multiplication tables for  $q = 5$.  You can see:

  • In the addition table there is exactly one zero in each row  (and also in each column). 
  • So for every  $z_i ∈ Z_5$  there is an  ${\rm Inv}_{\rm A} (z_i)$  that satisfies the condition  $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$:
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
  • In the multiplication table we leave the zero element  (first row and first column)  out of consideration.
  • In all other rows and columns of the lower table there is indeed exactly one each. 
  • From the condition $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$  one obtains:
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
  • Since both the required additive and multiplicative inverses exist   ⇒   $Z_5$ describes a Galois field $\rm GF(5)$  
  • Correct is the proposed solution 1.


(4)  From the blue addition table on the statement page,  we see that all numbers  $(0, \, 1, \, 2, \, 3, \, 4, \, 5)$  of the set $Z_6$  have an additive inverse

  ⇒   in each row  (and column)  there is exactly one zero.

  • On the other hand,  a multiplicative inverse  ${\rm Inv}_{\rm M}(z_i)$  exists only for  $z_i = 1$  and  $z_i = 5$,  viz.
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$
  • For  $z_i = 2, \ z_i = 3$ and $z_i = 4$,  we find no element  $z_j$,  so that  $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$.
  • Correct is the proposed solution 3   ⇒   the blue tables for  $q = 6$  do not yield a Galois field  $\rm GF(6)$.


(5)  Correct is the  proposed solution 2:

  • A finite number set  $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$  of natural numbers leads to a Galois field only if  $q$  is a prime number.
  • Of the number sets mentioned above,  this is true only for  $Z_{11}$.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_2.2:_Properties_of_Galois_Fields&oldid=48624"
  • Powered by MediaWiki