Difference between revisions of "Aufgaben:Exercise 2.2Z: Discrete Random Variables"
| Line 35: | Line 35: | ||
{Wie groß ist die Streuung der Zufallsgröße $b$? Setzen Sie $p = 0.25$. | {Wie groß ist die Streuung der Zufallsgröße $b$? Setzen Sie $p = 0.25$. | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_b \ = \ $ { 0.433 3% } |
| Line 43: | Line 43: | ||
| − | {Berechnen Sie den Mittelwert $m_d$ der Zufallsgröße $d$ für $p = 0.25$. | + | {Berechnen Sie den Mittelwert $m_d$ der Zufallsgröße $d$ für $p = 0.25$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $m_d\ = \ $ { -0.515--0.485 } |
{Wie groß ist der quadratische Mittelwert $m_{2d}$ dieser Zufallsgröße. | {Wie groß ist der quadratische Mittelwert $m_{2d}$ dieser Zufallsgröße. | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $m_{2d}\ = \ $ { 2.5 3% } |
{Wie groß ist die Streuung $\sigma_d$? | {Wie groß ist die Streuung $\sigma_d$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_d\ = \ $ { 1.5 3% } |
| Line 63: | Line 63: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Aufgrund der Symmetrie gilt: | '''(1)''' Aufgrund der Symmetrie gilt: | ||
| − | $$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$ | + | :$$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$ |
Daraus erhält man mit dem Satz von Steiner: | Daraus erhält man mit dem Satz von Steiner: | ||
| − | $$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm}bzw. \hspace{0.5cm}\it\sigma_a\hspace{0.15cm} \underline{=\rm 1}.$$ | + | :$$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm}bzw. \hspace{0.5cm}\it\sigma_a\hspace{0.15cm} \underline{=\rm 1}.$$ |
| + | |||
'''(2)''' Allgemein gilt für das Moment $k$–ter Ordnung: | '''(2)''' Allgemein gilt für das Moment $k$–ter Ordnung: | ||
| − | $$ m_{k}=(1-p)\cdot 0^{ k} + p\cdot 1^{k}= p.$$ | + | :$$ m_{k}=(1-p)\cdot 0^{ k} + p\cdot 1^{k}= p.$$ |
Daraus folgt mit $p = 1/4$: | Daraus folgt mit $p = 1/4$: | ||
| − | $$m_{b}= m_{2b}= p, \hspace{0.5cm} \sigma_{\it b}=\sqrt{p\cdot (1- p)}\hspace{0.15cm} \underline{=\rm 0.433} .$$ | + | :$$m_{b}= m_{2b}= p, \hspace{0.5cm} \sigma_{\it b}=\sqrt{p\cdot (1- p)}\hspace{0.15cm} \underline{=\rm 0.433} .$$ |
| + | |||
'''(3)''' Für die Zufallsgröße $c$ gilt: | '''(3)''' Für die Zufallsgröße $c$ gilt: | ||
| − | $$m_{\it c} = 0\hspace{0.1cm} ({\rm symmetrisch\hspace{0.1cm}um\hspace{0.1cm}0)}, \hspace{0.5cm}m_{2\it c}= {1}/{4}\cdot(-1)^2+{1}/{2}\cdot 0^2+{1}/{4}\cdot (1)^2={1}/{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sigma_{\it c}=\rm \sqrt{1/2}\hspace{0.15cm} \underline{=0.707}.$$ | + | :$$m_{\it c} = 0\hspace{0.1cm} ({\rm symmetrisch\hspace{0.1cm}um\hspace{0.1cm}0)}, \hspace{0.5cm}m_{2\it c}= {1}/{4}\cdot(-1)^2+{1}/{2}\cdot 0^2+{1}/{4}\cdot (1)^2={1}/{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sigma_{\it c}=\rm \sqrt{1/2}\hspace{0.15cm} \underline{=0.707}.$$ |
| + | |||
'''(4)''' Nach den allgemeinen Regeln für Erwartungswerte gilt mit $p = 0.25$: | '''(4)''' Nach den allgemeinen Regeln für Erwartungswerte gilt mit $p = 0.25$: | ||
| − | $$m_{\it d} = {\rm E}[a-2 b+c]= {\rm E}[a] \hspace{0.1cm} -\hspace{0.1cm}\rm 2 \hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}[ b]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}[ c] = m_{ a}\hspace{0.1cm}-\hspace{0.1cm}2\hspace{0.05cm}\cdot\hspace{0.05cm} m_{\it b}\hspace{0.1cm}+\hspace{0.1cm} m_{\it c} = 0-2\hspace{0.05cm}\cdot\hspace{0.05cm} p + 0 \hspace{0.15cm} \underline{= -0.5}.$$ | + | :$$m_{\it d} = {\rm E}\big[a-2 b+c\big]= {\rm E}\big[a\big] \hspace{0.1cm} -\hspace{0.1cm}\rm 2 \hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[ c\big] = m_{ a}\hspace{0.1cm}-\hspace{0.1cm}2\hspace{0.05cm}\cdot\hspace{0.05cm} m_{\it b}\hspace{0.1cm}+\hspace{0.1cm} m_{\it c} = 0-2\hspace{0.05cm}\cdot\hspace{0.05cm} p + 0 \hspace{0.15cm} \underline{= -0.5}.$$ |
| − | '''(5)''' Analog zur Teilaufgabe (4) erhält man für den quadratischen Mittelwert: | + | |
| − | $$m_{2d}= {\rm E}[( a-2b+c)^{\rm 2}] = {\rm E}[a^{\rm 2}]\hspace{0.1cm}+\hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}[ b^{\rm 2}]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}[c^{\rm 2}]\hspace{0.1cm} - \hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}[a\hspace{0.05cm}\cdot \hspace{0.05cm}b]\hspace{0.1cm}+\hspace{0.1cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}[ a\hspace{0.05cm}\cdot \hspace{0.05cm}c]\hspace{0.1cm}-\hspace{0.1cm} 4\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}[ b\hspace{0.05cm}\cdot \hspace{0.05cm}c].$$ | + | '''(5)''' Analog zur Teilaufgabe '''(4)''' erhält man für den quadratischen Mittelwert: |
| + | :$$m_{2d}= {\rm E}\big[( a-2b+c)^{\rm 2}\big] = {\rm E}\big[a^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[c^{\rm 2}\big]\hspace{0.1cm} - \hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[a\hspace{0.05cm}\cdot \hspace{0.05cm}b\big]\hspace{0.1cm}+\hspace{0.1cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ a\hspace{0.05cm}\cdot \hspace{0.05cm}c\big]\hspace{0.1cm}-\hspace{0.1cm} 4\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ b\hspace{0.05cm}\cdot \hspace{0.05cm}c\big].$$ | ||
Da aber $a$ und $b$ statistisch voneinander unabhängig sind, gilt auch: | Da aber $a$ und $b$ statistisch voneinander unabhängig sind, gilt auch: | ||
| − | $${\rm E}[a\cdot b] = {\rm E}[ a] \cdot {\rm E}[ b]= m_{ a}\cdot m_{ b} = 0, \hspace{0.1cm} {\rm da}\hspace{0.1cm} m_{ a}=\rm 0.$$ | + | :$${\rm E}\big[a\cdot b\big] = {\rm E}\big[ a\big] \cdot {\rm E}\big[ b\big]= m_{ a}\cdot m_{ b} = 0, \hspace{0.1cm} {\rm da}\hspace{0.1cm} m_{ a}=\rm 0.$$ |
Gleiches gilt für die anderen gemischten Terme. Daher erhält man mit $p = 0.25$: | Gleiches gilt für die anderen gemischten Terme. Daher erhält man mit $p = 0.25$: | ||
| − | $$ m_{2 d}=m_{2 a}+4\cdot m_{ 2 b}+m_{ 2 c}=1+4\cdot p+0.5\hspace{0.15cm} \underline{=\rm 2.5}.$$ | + | :$$ m_{2 d}=m_{2 a}+4\cdot m_{ 2 b}+m_{ 2 c}=1+4\cdot p+0.5\hspace{0.15cm} \underline{=\rm 2.5}.$$ |
| + | |||
| − | '''(6)''' Für allgemeines $p$ bzw. für $p = 0.25$ ergibt sich: | + | '''(6)''' Für allgemeines $p$ bzw. für $p = 0.25$ ergibt sich: |
| − | $$\sigma_{\it d}^{\rm 2}=1.5+4\cdot p - 4 \cdot p^{\rm 2}=2.25 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{d}\hspace{0.15cm} \underline{=\rm 1.5}.$$ | + | :$$\sigma_{\it d}^{\rm 2}=1.5+4\cdot p - 4 \cdot p^{\rm 2}=2.25 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{d}\hspace{0.15cm} \underline{=\rm 1.5}.$$ |
| − | Die maximale Varianz ergäbe sich für $p = 0.50$ zu $\sigma_{\it d}^{\rm 2}=2.50$. | + | Die maximale Varianz ergäbe sich für $p = 0.50$ zu $\sigma_{\it d}^{\rm 2}=2.50$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 18:26, 2 August 2018
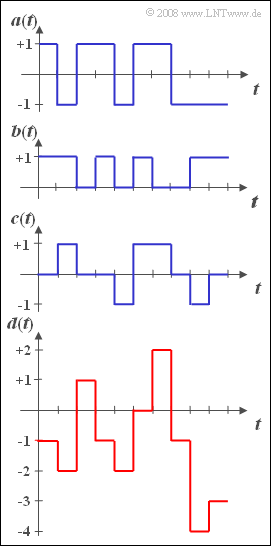
Gegeben seien drei diskrete Zufallsgrößen $a$, $b$ und $c$, die als die Momentanwerte der dargestellten Signale definiert seien. Diese besitzen folgende Eigenschaften:
- Die Zufallsgröße $a$ kann die Werte $+1$ und $-1$ mit gleicher Wahrscheinlichkeit annehmen.
- Auch die Zufallsgröße $b$ ist zweipunktverteilt, aber mit ${\rm Pr}(b = 1) = p$ und ${\rm Pr}(b = 0) = 1 - p$.
- Die Wahrscheinlichkeiten von $c$ seien ${\rm Pr}(c = 0) = 1/2$ und ${\rm Pr}(c = +1) = Pr(c = -1) =1/4$.
- Zwischen den drei Zufallsgrößen $a$, $b$ und $c$ bestehen keine statistischen Abhängigkeiten.
- Aus den Zufallsgrößen $a$, $b$ und $c$ wird eine weitere Zufallsvariable $d=a-2 b+c$ gebildet.
Die Grafik zeigt Ausschnitte dieser vier Zufallsgrößen. Es ist zu erkennen, dass $d$ alle ganzzahligen Werte zwischen $-4$ und $+2$ annehmen kann.
Hinweise:
- Die Aufgabe gehört zum Kapitel Momente einer diskreten Zufallsgröße.
- Eine Zusammenfassung der Theamatik bietet das Lernvideo Momentenberechnung bei diskreten Zufallsgrößen.
Fragebogen
Musterlösung
- $$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$
Daraus erhält man mit dem Satz von Steiner:
- $$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm}bzw. \hspace{0.5cm}\it\sigma_a\hspace{0.15cm} \underline{=\rm 1}.$$
(2) Allgemein gilt für das Moment $k$–ter Ordnung:
- $$ m_{k}=(1-p)\cdot 0^{ k} + p\cdot 1^{k}= p.$$
Daraus folgt mit $p = 1/4$:
- $$m_{b}= m_{2b}= p, \hspace{0.5cm} \sigma_{\it b}=\sqrt{p\cdot (1- p)}\hspace{0.15cm} \underline{=\rm 0.433} .$$
(3) Für die Zufallsgröße $c$ gilt:
- $$m_{\it c} = 0\hspace{0.1cm} ({\rm symmetrisch\hspace{0.1cm}um\hspace{0.1cm}0)}, \hspace{0.5cm}m_{2\it c}= {1}/{4}\cdot(-1)^2+{1}/{2}\cdot 0^2+{1}/{4}\cdot (1)^2={1}/{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sigma_{\it c}=\rm \sqrt{1/2}\hspace{0.15cm} \underline{=0.707}.$$
(4) Nach den allgemeinen Regeln für Erwartungswerte gilt mit $p = 0.25$:
- $$m_{\it d} = {\rm E}\big[a-2 b+c\big]= {\rm E}\big[a\big] \hspace{0.1cm} -\hspace{0.1cm}\rm 2 \hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[ c\big] = m_{ a}\hspace{0.1cm}-\hspace{0.1cm}2\hspace{0.05cm}\cdot\hspace{0.05cm} m_{\it b}\hspace{0.1cm}+\hspace{0.1cm} m_{\it c} = 0-2\hspace{0.05cm}\cdot\hspace{0.05cm} p + 0 \hspace{0.15cm} \underline{= -0.5}.$$
(5) Analog zur Teilaufgabe (4) erhält man für den quadratischen Mittelwert:
- $$m_{2d}= {\rm E}\big[( a-2b+c)^{\rm 2}\big] = {\rm E}\big[a^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[c^{\rm 2}\big]\hspace{0.1cm} - \hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[a\hspace{0.05cm}\cdot \hspace{0.05cm}b\big]\hspace{0.1cm}+\hspace{0.1cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ a\hspace{0.05cm}\cdot \hspace{0.05cm}c\big]\hspace{0.1cm}-\hspace{0.1cm} 4\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ b\hspace{0.05cm}\cdot \hspace{0.05cm}c\big].$$
Da aber $a$ und $b$ statistisch voneinander unabhängig sind, gilt auch:
- $${\rm E}\big[a\cdot b\big] = {\rm E}\big[ a\big] \cdot {\rm E}\big[ b\big]= m_{ a}\cdot m_{ b} = 0, \hspace{0.1cm} {\rm da}\hspace{0.1cm} m_{ a}=\rm 0.$$
Gleiches gilt für die anderen gemischten Terme. Daher erhält man mit $p = 0.25$:
- $$ m_{2 d}=m_{2 a}+4\cdot m_{ 2 b}+m_{ 2 c}=1+4\cdot p+0.5\hspace{0.15cm} \underline{=\rm 2.5}.$$
(6) Für allgemeines $p$ bzw. für $p = 0.25$ ergibt sich:
- $$\sigma_{\it d}^{\rm 2}=1.5+4\cdot p - 4 \cdot p^{\rm 2}=2.25 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{d}\hspace{0.15cm} \underline{=\rm 1.5}.$$
Die maximale Varianz ergäbe sich für $p = 0.50$ zu $\sigma_{\it d}^{\rm 2}=2.50$.