Difference between revisions of "Aufgaben:Exercise 2.3: Algebraic Sum of Binary Numbers"
| Line 3: | Line 3: | ||
}} | }} | ||
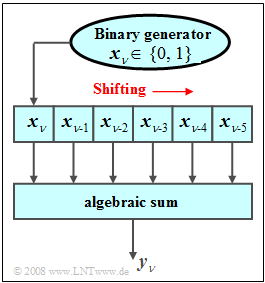
| − | [[File: | + | [[File:EN_Sto_A_2_3_neu.png|right|frame|Considered random generator]] |
A random number generator outputs a binary random number $x_\nu$ at each clock time $(\nu)$ , which can be $0$ or $1$ . | A random number generator outputs a binary random number $x_\nu$ at each clock time $(\nu)$ , which can be $0$ or $1$ . | ||
*The value "1" occurs with probability $p = 0.25$ . | *The value "1" occurs with probability $p = 0.25$ . | ||
Revision as of 17:47, 10 December 2021
A random number generator outputs a binary random number $x_\nu$ at each clock time $(\nu)$ , which can be $0$ or $1$ .
- The value "1" occurs with probability $p = 0.25$ .
- The individual values $x_\nu$ are statistically independent of each other.
The binary numbers are stored in a shift register withnbsp; $I = 6$ memory cells.
At each clock instant, the contents of this shift register are shifted one place to the right and the algebraic sum $y_\nu$ of the shift register contents is formed in each case:
- $$y_{\nu}=\sum\limits_{i=0}^{5}x_{\nu-i}=x_{\nu}+x_{\nu-1}+\ \text{...} \ +x_{\nu-5}.$$
Hints:
- The exercise belongs to the chapter binomial distribution.
- To check your results you can use the interactive applet Binomial and Poisson distribution .
Questions
Solution
- $$y_{\nu}\in\{0,1,\ \text{...} \ ,6\}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} y_{\rm max} \hspace{0.15cm} \underline{= 6}.$$
(2) There is a binomial distribution. Therefore, with $p = 0.25$:
- $${\rm Pr}(y =0)=(1-p)^{\it I}=0.75^6=0.178,$$
- $${\rm Pr}(y=1)=\left({ I \atop {1}}\right)\cdot (1-p)^{I-1}\cdot p= \rm 6\cdot 0.75^5\cdot 0.25=0.356,$$
- $${\rm Pr}(y=2)=\left({ I \atop { 2}}\right)\cdot (1-p)^{I-2}\cdot p^{\rm 2}= \rm 15\cdot 0.75^4\cdot 0.25^2=0.297,$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}(y>2)=1-{\rm Pr}(y=0)-{\rm Pr}( y=1)-{\rm Pr}( y=2)\hspace{0.15cm} \underline{=\rm 0.169}.$$
(3) According to the general equation, the mean of the binomial distribution is:
- $$m_y= I\cdot p\hspace{0.15cm} \underline{=\rm 1.5}.$$
(4) Accordingly, for the dispersion of the binomial distribution:
- $$\sigma_y=\sqrt{ I \cdot p \cdot( 1- p)} \hspace{0.15cm} \underline{= \rm 1.061}.$$
(5) Correct is the proposed solution 2:
- If $y_\nu = 0$, then only the values $0$ and $1$ can follow at the next time point, but not $2$, ... , $6$.
- That is: The sequence $ \langle y_\nu \rangle$ has (strong) statistical bindings.
(6) The probability we are looking for is identical to the probability that the new binary symbol is equal to the symbol dropped out of the shift register. It follows that:
- $${\rm Pr} (y_{\nu} = \mu\hspace{0.05cm}| \hspace{0.05cm} y_{\nu-{1}} = \mu) = {\rm Pr}(x_{\nu}= x_{\nu-6}). $$
- Since the symbols $x_\nu$ are statistically independent of each other, we can also write for this:
- $${\rm Pr}(x_{\nu} = x_{\nu-6}) = {\rm Pr}\big[(x_{\nu}= 1)\hspace{0.05cm}\cap\hspace{0.05cm}(x_{\nu-6}= 1)\hspace{0.05cm}\cup \hspace{0.05cm}(x_\nu=0)\hspace{0.05cm}\cap\hspace{0.05cm}(x_{\nu-6} =0)\big]= p^{2}+(1- p)^{2}=\rm 0.25^2 + 0.75^2\hspace{0.15cm} \underline{ = 0.625}. $$