Aufgaben:Exercise 2.5: Half-Wave Rectification

• Return to book

Gleichgerichtete Cosinusfunktionen

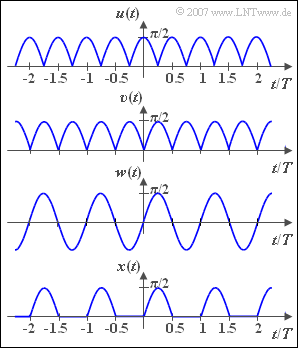
We are looking for the Fourier coefficients of the signal  $x(t)$, sketched below, which results from the one-way rectification of the sinusoidal signal  $w(t)$  with amplitude  $\pi /2$ .

The Fourier series representation of the signal  $u(t)$ sketched above is assumed to be known. This was already determined in  Aufgabe 2.4 . Taking into account the amplitude  $\pi /2$  the following applies:

$$u(t)=1+\frac{2}{3} \cdot \cos(\omega_1t)-\frac{2}{15}\cdot \cos(2\omega_1t)+\frac{2}{35}\cdot \cos(3\omega_1t)-\dots$$

It should be noted:

• The fundamental angular frequency is denoted by  $\omega_1$ . But since the period of the signals  $u(t)$  and  $v(t)$  is  $T/2$ ,   $\omega_1 = 2\pi /(T/2) = 4 \pi /T$.
• Because in this task the signals  $u(t)$,  $w(t)$  and  $x(t)$  are to be related to each other, the signal  $u(t)$  must also be represented with the period duration  $T$  of the signal  $x(t)$ .
• With  $\omega_0 = 2\pi /T = \omega_1/2$  the same applies:

$$u(t)=1+\frac{2}{3} \cdot \cos(2\omega_0t)-\frac{2}{15} \cdot \cos(4\omega_0t)+\frac{2}{35} \cdot \cos(6\omega_0t)-\dots$$

For the Fourier coefficients this means:

• The DC coefficient results in  $A_0 = 1$,
• All sine coefficients are  $B_n = 0$,
• The cosine coefficients with odd  $n = 1, \ 3, \ 5, \dots$ are all  $0$,
• The cosine coefficients with even  $n = 2, \ 4, \ 6, \dots$ are not equal to  $0$ :

$$A_n=(-1)^{\hspace{0.01cm}n/2+1}\frac{2}{n^2-1}.$$

This results in the following numerical values:

$$A_1=A_3=A_5=\dots=0,$$

$$A_2=2/3; \;A_4=-2/15;\;A_6=2/35;\;A_8=-2/63.$$

Hints:

• This exercise belongs to the chapter  Fourierreihe.
• You can find a compact summary of the topic in the two learning videos

Zur Berechnung der Fourierkoeffizienten,

Eigenschaften der Fourierreihendarstellung.

Questions

1

Calculate the Fourier coefficients of the signal  $v(t)$. What is the value of the coefficient  $A_2$?

$v(t)$:   $A_2\ = \ $

2

Calculate the Fourier coefficients of the signal  $w(t)$. What is the value of the coefficient  $B_1$?

$w(t)$:  $B_1\ = \ $

3

How can  $x(t)$  be composed of  $v(t)$  and  $w(t)$ ? Give the corresponding Fourier coefficients of the signal  $x(t)$  in particular

$x(t)$:  $A_0\ = \ $

$\hspace{1cm}B_1\ = \ $

$\hspace{1cm}A_2\ = \ $

Solution

Solution

(1)  Auch das verschobene Signal  $v(t)$  ist gerade und alle Sinuskoeffizienten sind dementsprechend Null.

• Am Gleichsignalkoeffizienten ändert sich ebenfalls nichts:  $A_0 = 1$.

• Aus den Signalverläufen ist zu erkennen, dass  $v(t) = u(t - T/4)$  gilt: 

$$v(t)=1+\frac{2}{3}\cdot \cos(2\omega_0(t-\frac{T}{4}))-\frac{2}{15}\cdot \cos(4\omega_0(t-\frac{T}{4}))+\frac{2}{35}\cdot \cos(6\omega_0(t-\frac{T}{4}))-\dots$$

• Die Cosinusterme können nun mit  $\omega_0 \cdot T = 2 \pi$  umgeformt werden: 

$$\cos(2\omega_0(t-\frac{T}{4}))=\cos(2\omega_0t-\pi)=-\cos(2\omega_0t),$$

$$\cos(4\omega_0(t-\frac{T}{4}))=\cos(4\omega_0t-2\pi)=\cos(4\omega_0t),$$

$$\cos(6\omega_0(t-\frac{T}{4}))=\cos(6\omega_0t-3\pi)=-\cos(6\omega_0t).$$

• Damit erhält man für die Fourierreihe:

$$v(t)=1-{2}/{3}\cdot \cos(2\omega_0t)-{2}/{15}\cdot \cos(4\omega_0t)-{2}/{35}\cdot \cos(6\omega_0t)-\dots$$

bzw. für die Cosinuskoeffizienten mit geradzahligem  $n$:

$$A_n=\frac{-2}{n^2-1}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}A_2=-\hspace{-0.05cm}2/3 \hspace{0.1cm}\underline{= -\hspace{-0.05cm}0.667}.$$

(2)  Wegen  $w(t) = \pi /2 \cdot \sin(\omega_0 t)$  sind alle Fourierkoeffizienten außer  $B_1 = \pi /2 \hspace{0.1cm}\underline{=1.571}$  gleich Null.

(3)  Aus der grafischen Darstellung erkennt man den Zusammenhang  $x(t)={1}/{2} \cdot \big [v(t)+w(t) \big].$ Das bedeutet:

$$x(t)=\frac{1}{2}+\frac{\pi}{4}\cdot \sin(\omega_0 t)-\frac{1}{3}\cdot \cos(2\omega_0 t)-\frac{1}{15}\cdot \cos(4\omega_0 t)-\frac{1}{35}\cdot \cos(6\omega_0 t)-\ldots$$

• Die gesuchten Fourierkoeffizienten sind somit:

$$A_0 \hspace{0.1cm}\underline{=0.5},\hspace{1cm} B_1 = \pi /4 \hspace{0.1cm}\underline{= 0.785},\hspace{1cm} A_2\hspace{0.1cm}\underline{ = -0.333}.$$