Difference between revisions of "Aufgaben:Exercise 2.5: Scatter Function"
m (Javier verschob die Seite Exercises:Exercise 2.5: Scatter Function nach Exercise 2.5: Scatter Function) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID2164__Mob_A_2_5.png|right|frame|Verzögerungs–Doppler–Funktion]] | [[File:P_ID2164__Mob_A_2_5.png|right|frame|Verzögerungs–Doppler–Funktion]] | ||
| − | + | For the mobile radio channel as a time-variant system, there are a total of four system functions that are linked with each other via the Fourier transformation. With the nomenclature formalized in our learning tutorial these: | |
| − | * | + | * the time-variant impulse response $h(\tau, \hspace{0.05cm}t)$, which we also refer to here as $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ , |
| − | * | + | * the delay–Doppler–function $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$, |
| − | * | + | * the frequency–Doppler–function $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$, |
| − | * | + | * the time variant transfer function $\eta_{\rm FZ}(f,\hspace{0.05cm}t)$ or $H(f, \hspace{0.05cm}t)$. |
| − | + | The indices represent the <b>V</b>delay $\tau$, the <b>Z</b>time $t$, the <b>F</b>frequency $f$ and the <b>D</b>oppler frequency $f_{\rm D}$. | |
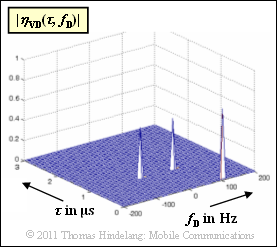
| − | + | Given is the delay–Doppler–function $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$ according to the upper graphic: | |
| − | + | $$\eta_{\rm VD}(\thaw, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \delta (\dew) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})-$$ | |
| − | :$$\hspace{1.75cm} \ - \ \hspace{-0.1cm} \frac{1}{2} \cdot \delta (\ | + | :$$\hspace{1.75cm} \ - \ \hspace{-0.1cm} \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})- |
| − | \frac{1}{2} \cdot \delta (\ | + | \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In the literature $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ often also called <i>Scatter–function</i> and denoted with $s(\tau, \hspace{0.05cm}f_{\rm D})$ . |
| − | In | + | In this task, the associated delay–time–function $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$ and the frequency–Doppler–function $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$ are to be determined. |
| Line 28: | Line 28: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * This task should clarify the subject matter of the chapter [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSSUS–Kanalmodell]]. |
| − | * | + | * The relationship between the individual system functions is given in the [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell#Verallgemeinerte_Systemfunktionen_zeitvarianter_Systeme|graph on the first page]] of this chapter. |
| − | * | + | *Note that the magnitude function $|\eta_{\rm VD}(\tau, \hspace{0.05cm} f_{\rm D})|$ is shown above, so negative weights of the Dirac functions cannot be recognized. |
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | + | Which $\tau$–values does the 2D–impulse response $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$ shares? At | |
|type="[]"} | |type="[]"} | ||
+ $\tau = 0$, | + $\tau = 0$, | ||
+ $\tau = 1 \ \rm µ s$, | + $\tau = 1 \ \rm µ s$, | ||
| − | - | + | - other $\tau$–values. |
| − | { | + | {Calculate $|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm}t)|$. Which of the following statements apply? |
|type="()"} | |type="()"} | ||
| − | + $|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm} t)|$ | + | + $|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm} t)|$ is independent of $t$. |
| − | - | + | - The following applies $\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$. |
| − | - | + | - It applies $\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$. |
| − | { | + | {Calculate $|\eta_{\rm VZ}(\dew = 1 \ {\rm µ s},\hspace{0.05cm} t)|$. Which of the statements apply? |
|type="()"} | |type="()"} | ||
| − | - $|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$ | + | - $|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$ is independent of $t$. |
| − | + | + | + It applies $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$. |
| − | - | + | - It applies $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$. |
| − | { | + | {View now the frequency–Doppler–display $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$. For which $f_{\rm D}$–Values is this function not equal to zero? For |
|type="[]"} | |type="[]"} | ||
- $f_{\rm D} = 0$, | - $f_{\rm D} = 0$, | ||
| Line 61: | Line 61: | ||
- $f_{\rm D} = ± 100 \ \rm Hz$. | - $f_{\rm D} = ± 100 \ \rm Hz$. | ||
| − | { | + | {Which of the following statements apply to $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$? |
|type="()"} | |type="()"} | ||
| − | + $|\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D} = 100 \ \rm Hz)|$ | + | + $|\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D} = 100 \ \rm Hz)|$ is independent of $f_{\rm D}$. |
| − | - | + | - It holds $\eta_{\rm FD}(f, \hspace{0.05cm} f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \cos {(2\pi t_0 f)}$. |
| − | - | + | - It applies $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \sin {(2\pi t_0 f)}$. |
| − | { | + | {How do you get the time variant transfer function $\eta_{\rm FZ}(f, \hspace{0.05cm}t)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - By Fourier transformation of $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$ regarding $\tau$. |
| − | + | + | + By Fourier transformation of $\eta_{\rm VZ}(\thaw, \hspace{0.05cm}t)$ relative to $\thaw$. |
| − | + | + | + By Fourier inverse transformation of $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$ relative to $f_{\rm D}$. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
| − | {{ML-Kopf}} | + | {{{ML-Kopf}} |
| − | '''(1)''' | + | '''(1)''' The time variant impulse response $h(\tau, \hspace{0.05cm} t) = \eta_{\rm VZ}(\tau, \hspace{0. 05cm} t)$ is the Fourier inverse transform of the delay–Doppler–function $\eta_{\rm VD}(\thaw,\hspace{0.05cm} f_{\rm D}) = s(\thaw, \hspace{0.05cm} f_{\rm D})$: |
| − | + | $$\eta_{\rm VZ}(\thaw, \hspace{0.05cm} t) | |
| − | \hspace{0.2cm} \stackrel{t, \hspace{0.02cm}f_{\rm D}}{\circ | + | \hspace{0.2cm} \stackrel{t, \hspace{0.02cm}f_{\rm D}{\circ}{\circ}!-\!-\!-\!-\!-\!\bullet} \hspace{0.2cm} \eta_{\rm VD}(\thaw, f_{\rm D})\hspace{0.05cm}.$$ |
| − | * | + | *Accordingly, $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ is identical for all values of $\tau$ $0$, for which no shares can be recognized in the scatter–function $\eta_{\rm VD}(\tau, f_{\rm D})$. |
| − | * | + | *The <u>solutions 1 and 2</u> are therefore correct: Only for $\tau = 0$ and $\tau = 1 \ \ \rm \mu s$ the time variant impulse response has finite values. |
| − | '''(2)''' | + | '''(2)''' For the delay $\tau = 0$ the scatter–function ($\eta_{\rm VD}$) consists of a single Dirac at $f_{\rm D} = 100 \ \rm Hz$. |
| − | * | + | *For the searched time function is valid according to the second Fourier integral: |
| − | + | $$\eta_{\rm VZ}(\tau = 0, t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \int\limits_{-\infty}^{+\infty} \delta (f_{\rm D} - 100\,{\rm Hz}) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}f_{\rm D} =\frac{1}{\sqrt{2}} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi t \hspace{0.05cm}\cdot \hspace{0.05cm}100\,{\rm Hz}} .$$ | |
| − | * | + | *The correct solution is therefore <u>solution 1</u>. |
| − | '''(3)''' | + | '''(3)''' For the delay time $\tau = 1 \ \ \rm µ s$ the delay–Doppler–function consists of two Dirac functions at $±50 \ \rm Hz$, each with the weight $-0.5$. |
| − | * | + | *The time function thus results in |
| − | + | $$\eta_{\rm VZ}(\tau = 1\,{\rm \mu s}, t) = - \cos( 2 \pi t \cdot 50\,{\rm Hz})\hspace{0.05cm}.$ | |
| − | * | + | *This function can be represented with $A = -1$ and $f_0 = 50 \ \rm Hz$ according to <u>solution 2</u>. |
| − | '''(4)''' | + | '''(4)''' The three Dirac functions $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ are at the Doppler frequencies $+100 \ \rm Hz$, $+50 \ \rm Hz$ and $-50 \ \rm Hz$. |
| − | * | + | *For all other Doppler frequencies, therefore, $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}) must also be \equiv 0$. |
| − | * | + | *The <u>solution is therefore correct here the <u>solution 2</u>. |
| − | '''(5)''' | + | '''(5)'''' If one looks at the scatter–function $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ in the direction of the $\tau$–axis, one recognizes only one Dirac function each at the Doppler frequencies $100 \ \rm Hz$ and $±50 \ \rm Hz$. |
| − | * | + | *Here, depending on $f$, complex exponential oscillations with constant magnitude result in each case (from which it follows that the <u>solution 1</u> is correct): |
| − | + | $$|\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 100\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{\sqrt{2}} = {\rm const.}$$ | |
| − | + | $$| \eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}= \pm 50\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5 = {\rm const.}$$ | |
| − | [[File: | + | [[File:P_ID2168__Mob_A_2_5e_new.png|right|frame|interrelation of all system functions]] |
| − | '''(6)''' | + | '''(6)''' As can be seen from the given [[Mobile_Communications/The_GWSSUS%E2%80%93Channel Model#Generalized_System Functions_Time-Variant_Systems|Graphics]], the <u>solution alternatives 2 and 3</u> are applicable. |
| − | * | + | *The graphic shows all system functions. |
| − | * | + | *The Fourier correspondences (shown in green) illustrate the relationships between these system functions. |
| − | '' | + | ''Note:'' |
| − | + | Compare the time-variant transfer function $|\eta_{\rm FZ}(f, \hspace{0.05cm} t)|$ in the figure below right with the corresponding graphic for [[Tasks:Task_2.4:_2D-Transfer Function| Task 2.4]]: | |
| − | * | + | *The respective amount functions shown differ significantly, although $|\eta_{\rm VZ}(\tau, t)|$ is the same in both cases. |
| − | *In | + | *In task 2.4, a cosine was implicitly assumed for $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, t)$, here a minus–cosine function. |
| − | * | + | *The (not explicitly) specified delay–Doppler function for task 2.4 was |
| − | + | $$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \delta (\dew) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})+$ | |
| − | + | $$\hspace{2cm}+\hspace{0.22cm}\frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})+ $ | |
| − | + | $$\hspace{2cm}+\hspace{0.22cm} \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Comparison with the equation on the [[Tasks:2.5_Scatter-Function|Specifications]] shows that only the signs of the Diracs have changed at $\tau = 1 \ \rm µ s$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:48, 15 April 2020
For the mobile radio channel as a time-variant system, there are a total of four system functions that are linked with each other via the Fourier transformation. With the nomenclature formalized in our learning tutorial these:
- the time-variant impulse response $h(\tau, \hspace{0.05cm}t)$, which we also refer to here as $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ ,
- the delay–Doppler–function $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$,
- the frequency–Doppler–function $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$,
- the time variant transfer function $\eta_{\rm FZ}(f,\hspace{0.05cm}t)$ or $H(f, \hspace{0.05cm}t)$.
The indices represent the Vdelay $\tau$, the Ztime $t$, the Ffrequency $f$ and the Doppler frequency $f_{\rm D}$.
Given is the delay–Doppler–function $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$ according to the upper graphic: $$\eta_{\rm VD}(\thaw, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \delta (\dew) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})-$$
- $$\hspace{1.75cm} \ - \ \hspace{-0.1cm} \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})- \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) \hspace{0.05cm}.$$
In the literature $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ often also called Scatter–function and denoted with $s(\tau, \hspace{0.05cm}f_{\rm D})$ .
In this task, the associated delay–time–function $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$ and the frequency–Doppler–function $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$ are to be determined.
Notes:
- This task should clarify the subject matter of the chapter Das GWSSUS–Kanalmodell.
- The relationship between the individual system functions is given in the graph on the first page of this chapter.
- Note that the magnitude function $|\eta_{\rm VD}(\tau, \hspace{0.05cm} f_{\rm D})|$ is shown above, so negative weights of the Dirac functions cannot be recognized.
Questionnaire
Sample solution
{
- Accordingly, $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ is identical for all values of $\tau$ $0$, for which no shares can be recognized in the scatter–function $\eta_{\rm VD}(\tau, f_{\rm D})$.
- The solutions 1 and 2 are therefore correct: Only for $\tau = 0$ and $\tau = 1 \ \ \rm \mu s$ the time variant impulse response has finite values.
(2) For the delay $\tau = 0$ the scatter–function ($\eta_{\rm VD}$) consists of a single Dirac at $f_{\rm D} = 100 \ \rm Hz$.
- For the searched time function is valid according to the second Fourier integral:
$$\eta_{\rm VZ}(\tau = 0, t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \int\limits_{-\infty}^{+\infty} \delta (f_{\rm D} - 100\,{\rm Hz}) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}f_{\rm D} =\frac{1}{\sqrt{2}} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi t \hspace{0.05cm}\cdot \hspace{0.05cm}100\,{\rm Hz}} .$$
- The correct solution is therefore solution 1.
(3) For the delay time $\tau = 1 \ \ \rm µ s$ the delay–Doppler–function consists of two Dirac functions at $±50 \ \rm Hz$, each with the weight $-0.5$.
- The time function thus results in
$$\eta_{\rm VZ}(\tau = 1\,{\rm \mu s}, t) = - \cos( 2 \pi t \cdot 50\,{\rm Hz})\hspace{0.05cm}.$ *This function can be represented with $A = -1$ and $f_0 = 50 \ \rm Hz$ according to <u>solution 2</u>. '''(4)''' The three Dirac functions $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ are at the Doppler frequencies $+100 \ \rm Hz$, $+50 \ \rm Hz$ and $-50 \ \rm Hz$. *For all other Doppler frequencies, therefore, $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}) must also be \equiv 0$. *The <u>solution is therefore correct here the <u>solution 2</u>. '''(5)'''' If one looks at the scatter–function $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ in the direction of the $\tau$–axis, one recognizes only one Dirac function each at the Doppler frequencies $100 \ \rm Hz$ and $±50 \ \rm Hz$. *Here, depending on $f$, complex exponential oscillations with constant magnitude result in each case (from which it follows that the <u>solution 1</u> is correct): $$|\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 100\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{\sqrt{2}} = {\rm const.}$$ $$| \eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}= \pm 50\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5 = {\rm const.}$$ [[File:P_ID2168__Mob_A_2_5e_new.png|right|frame|interrelation of all system functions]] '''(6)''' As can be seen from the given [[Mobile_Communications/The_GWSSUS%E2%80%93Channel Model#Generalized_System Functions_Time-Variant_Systems|Graphics]], the <u>solution alternatives 2 and 3</u> are applicable. *The graphic shows all system functions. *The Fourier correspondences (shown in green) illustrate the relationships between these system functions. ''Note:'' Compare the time-variant transfer function $|\eta_{\rm FZ}(f, \hspace{0.05cm} t)|$ in the figure below right with the corresponding graphic for [[Tasks:Task_2.4:_2D-Transfer Function| Task 2.4]]: *The respective amount functions shown differ significantly, although $|\eta_{\rm VZ}(\tau, t)|$ is the same in both cases. *In task 2.4, a cosine was implicitly assumed for $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, t)$, here a minus–cosine function. *The (not explicitly) specified delay–Doppler function for task 2.4 was $$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \delta (\dew) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})+$ '"`UNIQ-MathJax40-QINU`"'\hspace{2cm}+\hspace{0.22cm} \frac{1}{2} \cdot \delta (\dew- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) \hspace{0.05cm}.$$ *Comparison with the equation on the [[Tasks:2.5_Scatter-Function|Specifications]] shows that only the signs of the Diracs have changed at $\tau = 1 \ \rm µ s$.