Difference between revisions of "Aufgaben:Exercise 2.6: Dimensions in GWSSUS"
From LNTwww
m (Text replacement - "power spectral density" to "power-spectral density") |
|||
| (27 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/The_GWSSUS_Channel_Model}} |
| − | [[File:P_ID2167__Mob_A_2_6.png|right|frame| | + | [[File:P_ID2167__Mob_A_2_6.png|right|frame|Overview of the GWSSUS functions]] |
| − | The mobile radio channel can be described in very general terms by four system functions, whereby the relationship between each | + | The mobile radio channel can be described in very general terms by four system functions, whereby the relationship between each pair of functions is described by |
* the Fourier transform or | * the Fourier transform or | ||
| − | * the Fourier | + | * the inverse Fourier transform. |
| − | + | We denote all of the functions with $\eta_{i_1i_2}$. The indices $i_1$ and $i_2$ are defined as follows: | |
| + | * $\boldsymbol{\rm V}$ $($because of German $\rm V\hspace{-0.05cm}$erzögerung$)$ stands for delay time $\tau$ $($index $i_1)$, | ||
| + | * $\boldsymbol{\rm F}$ stands for frequency $f$ $($index $i_1)$, | ||
| + | * $\boldsymbol{\rm Z}$ $($because of German $\rm Z\hspace{-0.05cm}$eit$)$ stands for the time $t$ $($index $i_2)$, | ||
| + | * $\boldsymbol{\rm D}$ stands for the Doppler frequency $f_{\rm D}$ $($index $i_2)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The relationship between the functions is shown in the diagram (yellow background). The Fourier correspondences are shown in green: | |
| − | The relationship between the functions is shown in the diagram (yellow background). The Fourier correspondences are shown in green: | + | * The transition from a circle filled with white to a circle filled with green corresponds to the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_First_Fourier_Integral|Fourier transform]]. |
| − | * The transition from a circle filled with white to a circle filled with green corresponds to | + | * The transition from a circle filled with green to a circle filled with white corresponds to the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_Second_Fourier_Integral|inverse Fourier transform]] (opposite direction). |
| − | * The transition from a circle filled with green to a circle filled with white corresponds to the [[ | ||
For example: | For example: | ||
| − | $$\eta_{\rm VZ}(\tau, t) | + | :$$\eta_{\rm VZ}(\tau, t) |
| − | \hspace{0.2cm} \stackrel{\ | + | \hspace{0.2cm} \stackrel{\tau, \hspace{0.02cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,t)\hspace{0.05cm}, |
\hspace{0.4cm}\eta_{\rm FZ}(f,t) | \hspace{0.4cm}\eta_{\rm FZ}(f,t) | ||
| − | \hspace{0.2cm} \stackrel{f, \hspace{0.02cm} | + | \hspace{0.2cm} \stackrel{f, \hspace{0.02cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.05cm}.$$ |
| − | *The correlation function $\varphi_{ | + | *The correlation function $\varphi_{i_1\hspace{0.02cm}i_2}$ and the power-spectral density $\it \Phi_{i_1\hspace{0.02cm}i_2}$ are provided with the same indices as the system function $\eta_{i_1\hspace{0.02cm}i_2}$. |
| − | *Correlation functions can be recognized by the red font in the lower graph and all power | + | *Correlation functions can be recognized by the red font in the lower graph and all power densitiy spectra are labeled in blue. The GWSSUS model is always assumed. |
| − | Let us consider here the system function $\eta_{\rm VZ}(\tau, t)$, i.e. the time variant impulse response $h(\tau, t)$. | + | Let us consider here the system function $\eta_{\rm VZ}(\tau, t)$, i.e. the time–variant impulse response $h(\tau, t)$. We define: |
| − | $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot | + | :$$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot |
\eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$ | \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$ | ||
| − | $$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 | + | :$$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| − | \varphi_{\rm VZ}(\ | + | \varphi_{\rm VZ}(\Delta \tau, \Delta t) \hspace{0.05cm}, $$ |
| − | $$\varphi_{\rm VZ}(\ | + | :$$\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.$$ |
| − | $${\it \ | + | :$${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)\hspace{0.05cm}. $$ |
| − | ''Note:'' This | + | ''Note:'' This exercise belongs to the chapter [[Mobile_Communications/The_GWSSUS_Channel_Model| The GWSSUS Channel Model]]. |
| Line 49: | Line 47: | ||
===Questionnaire=== | ===Questionnaire=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following specified dimensions of the system functions are correct? |
|type="[]"} | |type="[]"} | ||
| − | + $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$ | + | + $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$. |
| − | + $\eta_{\rm FZ}(f, t)$ | + | + $\eta_{\rm FZ}(f, t)$ is without unit. |
| − | + $\eta_{\rm VD}(\tau, f_{\rm D})$ | + | + $\eta_{\rm VD}(\tau, f_{\rm D})$ is without unit. |
| − | + $\eta_{\rm FD}(f, f_{\rm D})$ has the unit $[1/\rm Hz]$ | + | + $\eta_{\rm FD}(f, f_{\rm D})$ has the unit $[1/\rm Hz]$. |
| − | { | + | {Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - $\varphi_{\rm VZ}(\ | + | - $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ has the unit $[1/\rm s]$. |
| − | + ${\it \phi}_{\rm VZ}(\tau, {\rm \ | + | + ${\it \phi}_{\rm VZ}(\tau, {\rm \Delta} t)$ has the unit $[1/\rm s]$. |
+ ${\it \phi}_{\rm V}(\tau)$ has the unit $[1/\rm s]$. | + ${\it \phi}_{\rm V}(\tau)$ has the unit $[1/\rm s]$. | ||
| − | { | + | {Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
+ $\varphi_{\rm FZ}(\Delta f, \Delta t), \varphi_{\rm F}(\Delta f)$ and $\varphi_{\rm Z}(\Delta t)$ have no unit. | + $\varphi_{\rm FZ}(\Delta f, \Delta t), \varphi_{\rm F}(\Delta f)$ and $\varphi_{\rm Z}(\Delta t)$ have no unit. | ||
- ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ has the unit $[1/\rm s]$. | - ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ has the unit $[1/\rm s]$. | ||
| − | + ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ and ${\it \Phi}_{\rm D}(f_{\rm D})$ have the unit $[1/\rm Hz]$ each. | + | + ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ and ${\it \Phi}_{\rm D}(f_{\rm D})$ have the unit $[1/\rm Hz]$ each. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' <u>All statements are correct</u>: | '''(1)''' <u>All statements are correct</u>: | ||
| − | *$\eta_{\rm VZ}(\tau, t)$ is the time variant impulse response, for which the term $h(\tau, t)$ is also common. Like every impulse response, $h(\tau, t)$ has the unit $[1/\rm s]$. | + | *$\eta_{\rm VZ}(\tau, t)$ is the time-variant impulse response, for which the term $h(\tau, t)$ is also common. Like every impulse response, $h(\tau, t)$ has the unit $[1/\rm s]$. |
| − | *By Fourier | + | *By Fourier transform of the function $\eta_{\rm VZ}(\tau, t)$ with respect to the delay $\tau$ one obtains |
| − | $$\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau | + | :$$\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *Due to the integration over $\tau$ $($unit: $\rm s)$, the time-variant transfer function $\eta_{\rm FZ}(f, t)$ is dimensionless. <br>In some literature, $H(f, t)$ is also used instead of $\eta_{\rm FZ}(f, t)$. |
| − | *The delay–Doppler& | + | *The delay–Doppler representation $\eta_{\rm VD}(\tau, f_{\rm D})$ is dimensionless, too. This function results from the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ by Fourier transform with respect to $t$: |
| − | $$\eta_{\rm VD}(\tau, f_{\rm D}) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}t | + | :$$\eta_{\rm VD}(\tau, f_{\rm D}) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}t |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The function $\eta_{\rm FD}(t, f_{\rm D})$ | + | *The function $\eta_{\rm FD}(t, f_{\rm D})$ is obtained from the dimensionless functions $\eta_{\rm VD}(\tau, f_{\rm D})$ and $\eta_{\rm FZ}(f, t)$ respectively by a Fourier transform, which results in the unit $[\rm s] = [1/\rm Hz]$. |
| − | '''(2)''' | + | '''(2)''' <u>Solutions 2 and 3</u> are correct: |
| − | *The | + | *The auto-correlation $\rm (ACF)$ function is by definition the following expected value: |
| − | $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot | + | :$$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot |
\eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm}.$$ | \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm}.$$ | ||
| − | *Since the time variant impulse response $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$, its | + | *Since the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$, its ACF $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ has the unit $[1/\rm s^2]$, both in the general case $\varphi_{\rm VZ}(\tau_1, l_1, \tau_2, t_2)$ and with the GWSSUS case $\varphi_{\rm VZ}(\Delta \tau, \ \Delta t)$. |
| − | *The Dirac function $\delta(\ | + | *The Dirac function ${\rm \delta}(\Delta \tau)$ has the unit $[1/\rm s]$, since the integral over all $\tau$ $($with unit $[\rm s])$ must be $1$. Therefore, both the delay–time cross power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta \tau)$ and the delay power-spectral density ${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)$ have unit $[1/\rm s]$. |
| − | '''(3)''' | + | '''(3)''' <u>Statements 1 and 3</u> are correct: |
| − | * | + | *The function ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$ has unit $[1/\rm s]$. Its Fourier transform with respect to $\tau$ is $\varphi_{\rm FZ}(\Delta f, \Delta t)$, while its Fourier transform with respect to $t$ is ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$. Both $\varphi_{\rm FZ}(\Delta f, \Delta t)$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ are therefore without unit. |
| − | *The frequency–Doppler | + | *The frequency–Doppler cross power-spectral density has the unit $[\rm s] = [1/\rm Hz]$, because |
| − | $${\it \Phi}_{\rm FD}(\ | + | :$${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}. $$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^2.3 The GWSSUS Channel Model^]] |
Latest revision as of 13:41, 17 February 2022
The mobile radio channel can be described in very general terms by four system functions, whereby the relationship between each pair of functions is described by
- the Fourier transform or
- the inverse Fourier transform.
We denote all of the functions with $\eta_{i_1i_2}$. The indices $i_1$ and $i_2$ are defined as follows:
- $\boldsymbol{\rm V}$ $($because of German $\rm V\hspace{-0.05cm}$erzögerung$)$ stands for delay time $\tau$ $($index $i_1)$,
- $\boldsymbol{\rm F}$ stands for frequency $f$ $($index $i_1)$,
- $\boldsymbol{\rm Z}$ $($because of German $\rm Z\hspace{-0.05cm}$eit$)$ stands for the time $t$ $($index $i_2)$,
- $\boldsymbol{\rm D}$ stands for the Doppler frequency $f_{\rm D}$ $($index $i_2)$.
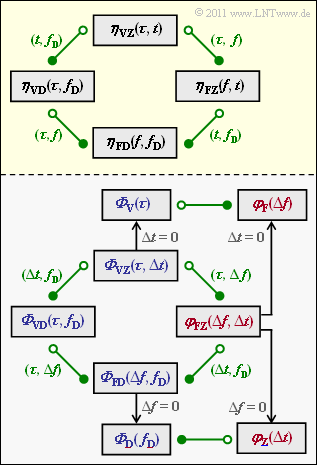
The relationship between the functions is shown in the diagram (yellow background). The Fourier correspondences are shown in green:
- The transition from a circle filled with white to a circle filled with green corresponds to the Fourier transform.
- The transition from a circle filled with green to a circle filled with white corresponds to the inverse Fourier transform (opposite direction).
For example:
- $$\eta_{\rm VZ}(\tau, t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.02cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,t)\hspace{0.05cm}, \hspace{0.4cm}\eta_{\rm FZ}(f,t) \hspace{0.2cm} \stackrel{f, \hspace{0.02cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.05cm}.$$
- The correlation function $\varphi_{i_1\hspace{0.02cm}i_2}$ and the power-spectral density $\it \Phi_{i_1\hspace{0.02cm}i_2}$ are provided with the same indices as the system function $\eta_{i_1\hspace{0.02cm}i_2}$.
- Correlation functions can be recognized by the red font in the lower graph and all power densitiy spectra are labeled in blue. The GWSSUS model is always assumed.
Let us consider here the system function $\eta_{\rm VZ}(\tau, t)$, i.e. the time–variant impulse response $h(\tau, t)$. We define:
- $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$
- $$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VZ}(\Delta \tau, \Delta t) \hspace{0.05cm}, $$
- $$\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.$$
- $${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)\hspace{0.05cm}. $$
Note: This exercise belongs to the chapter The GWSSUS Channel Model.
Questionnaire
Solution
(1) All statements are correct:
- $\eta_{\rm VZ}(\tau, t)$ is the time-variant impulse response, for which the term $h(\tau, t)$ is also common. Like every impulse response, $h(\tau, t)$ has the unit $[1/\rm s]$.
- By Fourier transform of the function $\eta_{\rm VZ}(\tau, t)$ with respect to the delay $\tau$ one obtains
- $$\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}. $$
- Due to the integration over $\tau$ $($unit: $\rm s)$, the time-variant transfer function $\eta_{\rm FZ}(f, t)$ is dimensionless.
In some literature, $H(f, t)$ is also used instead of $\eta_{\rm FZ}(f, t)$.
- The delay–Doppler representation $\eta_{\rm VD}(\tau, f_{\rm D})$ is dimensionless, too. This function results from the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ by Fourier transform with respect to $t$:
- $$\eta_{\rm VD}(\tau, f_{\rm D}) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}t \hspace{0.05cm}.$$
- The function $\eta_{\rm FD}(t, f_{\rm D})$ is obtained from the dimensionless functions $\eta_{\rm VD}(\tau, f_{\rm D})$ and $\eta_{\rm FZ}(f, t)$ respectively by a Fourier transform, which results in the unit $[\rm s] = [1/\rm Hz]$.
(2) Solutions 2 and 3 are correct:
- The auto-correlation $\rm (ACF)$ function is by definition the following expected value:
- $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm}.$$
- Since the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$, its ACF $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ has the unit $[1/\rm s^2]$, both in the general case $\varphi_{\rm VZ}(\tau_1, l_1, \tau_2, t_2)$ and with the GWSSUS case $\varphi_{\rm VZ}(\Delta \tau, \ \Delta t)$.
- The Dirac function ${\rm \delta}(\Delta \tau)$ has the unit $[1/\rm s]$, since the integral over all $\tau$ $($with unit $[\rm s])$ must be $1$. Therefore, both the delay–time cross power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta \tau)$ and the delay power-spectral density ${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)$ have unit $[1/\rm s]$.
(3) Statements 1 and 3 are correct:
- The function ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$ has unit $[1/\rm s]$. Its Fourier transform with respect to $\tau$ is $\varphi_{\rm FZ}(\Delta f, \Delta t)$, while its Fourier transform with respect to $t$ is ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$. Both $\varphi_{\rm FZ}(\Delta f, \Delta t)$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ are therefore without unit.
- The frequency–Doppler cross power-spectral density has the unit $[\rm s] = [1/\rm Hz]$, because
- $${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}. $$