Exercise 2.6Z: Signal-to-Noise Ratio

• Return to book

Diverse Power Density Spectra

In the following exercise, we assume:

• a cosine source signal:

$$ q(t) = 4 \,{\rm V} \cdot \cos(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm},$$

• DSB–AM by multiplication with

$$z(t) = 1 \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t )\hspace{0.05cm},$$

• a frequency-independent attenuation on the channel corresponding to  $α_{\rm K} = 10^{–4}$,
• additive white input noise with noise power density  $N_0 = 4 · 10^{–19} \ \rm W/Hz$,
• phase- and frequency-synchronous demodulation by multiplication with the same  $z(t)$  as at the transmitter,
• a rectangular low-pass at the synchronous demodulator with cutoff frequency  $f_{\rm E} = 5 \ \rm kHz$.

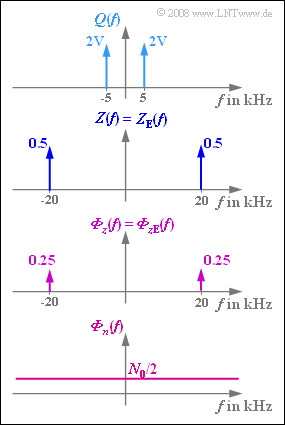
In the graph, these specifications are shown in the spectral domain. It should be explicitly mentioned that the power density spectrum  ${\it Φ}_z(f)$  of the cosine oscillation  $z(t)$  is composed of two Dirac lines at  $±f_{\rm T}$  zusammensetzt, as is the amplitude spectrum   $Z(f)$ , but with weight  $A^2/4$  instead of  $A/2$.  The amplitude should always be set to  $A=1$  in this exercise.

The sink signal  $v(t)$  is composed of the useful component  $α · q(t)$  and the noise component  $ε(t)$ .  Thus, the general rule for the signal-to-noise power ratio to be determined is:

$$ \rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon}\hspace{0.05cm}.$$

This important quality criterion is often abbreviated to  SNR  (  Signal–to–Noise–Ratio).

Hints:

• This exercise belongs to the chapter  Synchronous Demodulation.
• Particular reference is made to the pages  Calculating noise power  and  Relationship between $P_q$  and  $P_{\rm S}$.
• Please note that the variables  $α$  and  $α_{\rm K}$  need not be the same.
• All powers refer to a resistance of  $R = 50 \ \rm Ω$ with the exception of  (1) .
• For DSB-AM without a carrier, $P_q$  also represents the transmit power  $P_{\rm S}$ .

Questions

1

Berechnen Sie die Sendeleistung bezogen auf den Einheitswiderstand  $R = 1 \ \rm Ω$.

$P_q \ = \ $ $\ \rm V^2$

2

Wie groß ist die Leistung  $P_q$  in „Watt” für den Widerstand  $R = 50 \ \rm Ω$?

$P_q \ = \ $ $\ \rm W$

3

Welcher Dämpfungsfaktor  $α$  ergibt sich für das Gesamtsystem?

$α \ = \ $ $\ \cdot 10^{-4}$

4

Berechnen Sie die Leistungsdichte der Rauschkomponente  $ε(t)$  am Ausgang.  Wie groß ist der Wert bei  $f = 0$?  Es gelte  $H_{\rm E}(f = 0) = 1$.

${\it Φ}_ε(f = 0) \ = \ $ $\ \cdot 10^{-19} \ \rm W/Hz$

5

Wie groß ist die Rauschleistung im Sinkensignal?

$P_ε \ = \ $ $\ \cdot 10^{-15} \ \rm W$

6

Wie groß ist das Signal–zu–Rausch–Leistungsverhältnis (SNR) an der Sinke?  Welcher dB–Wert ergibt sich daraus?

$ρ_v \ = \ $

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Das Leistungsdichtespektrum eines Cosinussignals mit der Amplitude  $A$  besteht aus zwei Diraclinien, jeweils mit Gewicht  $A^2/4$.

• Die Leistung ergibt sich aus dem Integral über das LDS und ist somit gleich der Summe der beiden Diracgewichte.  Mit  $A = 4 \ \rm V$  erhält man somit für die Leistung des Quellensignals:

$$ P_q = \frac{A^2}{2} \hspace{0.15cm}\underline {= 8\,{\rm V^2}} \hspace{0.05cm}.$$

• Beim Modulationsverfahren „ZSB-AM ohne Träger” ist dies gleichzeitig die auf den Einheitswiderstand  $1\ \rm Ω$  bezogene Sendeleistung $P_{\rm S}$.

(2)  Nach den elementaren Gesetzen der Elektrotechnik gilt:

$$P_q = \frac{8\,{\rm V^2}}{50\,{\Omega}} \hspace{0.15cm}\underline {= 0.16\,{\rm W}} \hspace{0.05cm}.$$

(3)  Im Theorieteil wird gezeigt, dass bei idealen Voraussetzungen  $v(t) = q(t)$  gilt.  Zu berücksichtigen ist allerdings:

• Aus der Grafik erkennt man, dass  $Z_{\rm E}(f) = Z(f)$  gilt.  Damit hat das empfängerseitige Trägersignal  $z_{\rm E}(t)$  wie  $z(t)$  die Amplitude  $1$.
• Im Idealfall müsste aber das empfängerseitige Trägersignal  $z_{\rm E}(t)$  die Amplitude  $2$  besitzen.
• Deshalb gilt gilt hier $υ(t) = q(t)/2$.
• Berücksichtigt man weiter die Kanaldämpfung  $α_{\rm K} = 10^{–4}$, so erhält man das Endergebnis:   $α\hspace{0.15cm}\underline { = 0.5 · 10^{–4}}.$

(4)  Das Leistungsdichtespektrum des Produktes  $n(t) · z(t)$  ergibt sich aus der Faltung der beiden Leistungsdichtespektren von  $n(t)$  und  $z(t)$:

$$ {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) = {\it \Phi}_n (f) \star {\it \Phi}_{z }(f)= \frac{N_0}{2} \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]= N_0 \hspace{0.05cm}.$$

• Für das Leistungsdichtespektrum des Signals  $ε(t)$  nach dem Tiefpass erhält man eine Rechteckform mit dem gleichen Wert bei  $f = 0$:

$${\it \Phi}_\varepsilon (f) = {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) \cdot |H_{\rm E}(f)|^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\it \Phi}_\varepsilon (f=0)= N_0\hspace{0.15cm}\underline {= 4 \cdot 10^{-19}\,{\rm W/Hz}} \hspace{0.05cm}.$$

(5)  Die Rauschleistung ist das Integral über die Rauschleistungsdichte:

$$ P_{\varepsilon} = \int_{-f_{\rm E}}^{ + f_{\rm E}} {{\it \Phi}_\varepsilon (f)}\hspace{0.1cm}{\rm d}f = N_0 \cdot 2 f_{\rm E} = 4 \cdot 10^{-19}\,\frac{ \rm W}{\rm Hz} \cdot 10^{4}\,{\rm Hz} \hspace{0.15cm}\underline {= 4 \cdot 10^{-15}\,{\rm W}}\hspace{0.05cm}.$$

(6)  Aus den Ergebnissen der Teilaufgaben  (2),  (3)  und  (5)  folgt:

$$\rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon} = \frac{(0.5 \cdot 10^{-4})^2 \cdot 0.16\,{\rm W}}{4 \cdot 10^{-15}\,{\rm W}} \hspace{0.15cm}\underline {= 100000} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg }\hspace{0.1cm}\rho_{v } \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$