Aufgaben:Exercise 2.7Z: Coherence Bandwidth of the LTI Two-Path Channel

• Return to book

Two two-path channels

For the GWSSUS model, two parameters are given, which both statistically capture the resulting delay  $\tau$.  More information on the topic „Multipath Propagation” can be found in the section  Parameters of the GWSSUS model  of the theory part.

• The  delay spread  $T_{\rm V}$  is by definition equal to the standard deviation of the random variable  $\tau$.
  This can be determined from the probability density function  $f_{\rm V}(\tau)$.  The PDF  $f_{\rm V}(\tau)$  has the same shape as the delay power density spectrum  ${\it \Phi}_{\rm V}(\tau)$.
• The  coherence bandwidth  $B_{\rm K}$  describes the same situation in the frequency domain.
  It is defined as the value of $\Delta f$ at which the magnitude of the frequency correlation function  $\varphi_{\rm F}(\Delta f)$  first drops to half its maximum value:

$$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} {1}/{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| \hspace{0.05cm}.$$

The relationship between  ${\it \Phi}_{\rm V}(\tau)$  and  $\varphi_{\rm F}(\Delta f)$  is given by the Fourier transform:

$$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$

• Both definitions are only partially suitable for a time-invariant channel.
• For a time-invariant two-path channel (i.e. one with constant path weights according to the above graph), the following approximation for the coherence bandwidth is often used:

$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$

In this task we want to clarify

• why there are different definitions for the coherence bandwidth in the literature,
• which connection exists between  $B_{\rm K}$  and  $B_{\rm K}\hspace{0.01cm}'$,  and
• which definitions make sense for which boundary conditions.

Notes:

• This exercise belongs to the chapter  The GWSSUS Channel Model.
• This task also refers to some theory pages in chapter  Multi-Path Reception in Mobile Communications.

Questionnaire

1

What is the approximate coherence bandwidth  $B_{\rm K}\hspace{0.01cm}'$  for channels  $\rm A$  and  $\rm B$?

Channel  ${\rm A} \text{:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' \ = \ $ $\ \ \rm kHz$

Channel  ${\rm B} \text{:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' \ = \ $ $\ \ \rm kHz$

2

Let  $G$  be the weight of the second path.  What is the PDF  $f_{\rm V}(\tau)$?

	$f_{\rm V}(\tau) = \delta(\tau) + G \cdot \delta(\tau \, –\tau_0)$,
	$f_{\rm V}(\tau) = \delta(\tau) + G^2 \cdot \delta(\tau \, –\tau_0)$,
	$f_{\rm V}(\tau) = 1/(1 + G^2) \cdot \delta(\tau) + G^2/(1 + G^2) \cdot \delta(\tau \, –\tau_0)$.

3

Calculate the delay spread  $ T_{\rm V}$.

Channel  ${\rm A} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ $ $\ \rm µ s$

Channel  ${\rm B} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ $ $\ \rm µ s$

4

What is the coherence bandwidth  $B_{\rm K}$  of channel  ${\rm A}$ ?

	$B_{\rm K} = 333 \ \rm kHz$.
	$B_{\rm K} = 500 \ \rm kHz$.
	$B_{\rm K} = 1 \ \rm MHz$.
	$B_{\rm K}$  cannot be calculated according to this definition.

5

What is the coherence bandwidth  $B_{\rm K}$  of channel  ${\rm B}$ ?

	$B_{\rm K} = 333 \ \rm kHz$.
	$B_{\rm K} = 500 \ \rm kHz$.
	$B_{\rm K} = 1 \ \ \rm MHz$.
	$B_{\rm K}$  cannot be calculated according to this definition.

Solution

Solution

(1)  For both channels, the delay difference is  $\Delta \tau = \tau_{\rm max} \, - \tau_{\rm min} = 1 \ \ \rm µ s$.

• That's why both channels have the same value:

$$B_{\rm K}\hspace{0.01cm}' \ \ \underline {= 1000 \ \rm kHz}.$$

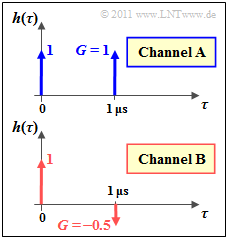
(2)  The graphs refer to the impulse response  $h(\tau)$.

• To obtain the delay–power density spectrum, the weights must be squared:

$${\it \Phi}_{\rm V}(\tau) = 1^2 \cdot \delta(\tau) + G^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$

• The integral of  ${\it \Phi}_{\rm V}(\tau)$  is therefore  $1 + G^2$.
• The probability density function  $\rm (PDF)$, however, must have „area $1$” $($i.e., the sum of the two Dirac weights must be $1)$.  From this follows:

$$f_{\rm V}(\tau) = \frac{1}{1 + G^2} \cdot \delta(\tau) + \frac{G^2}{1 + G^2} \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$

• Only solution 3 is correct.
• The first option does not describe the PDF  $f_{\rm V}(\tau)$, but the impulse response  $h(\tau)$.
• The second equation specifies the delay power density spectrum  ${\it \Phi}_{\rm V}(\tau)$.

(3)  For channel  $\rm A$  the two impulse weights are equal.  This means that the mean value  $m_{\rm V}$  and the standard deviation  $\sigma_{\rm V} = T_{\rm V}$  can be computed simply:

$$m_{\rm V} = \frac{\tau_0}{2} \hspace{0.15cm} {= 0.5\,{\rm µ s}}\hspace{0.05cm}, \hspace{0.2cm}T_{\rm V} = \sigma_{\rm V} =\frac{\tau_0}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm µ s}} \hspace{0.05cm}.$$

For channel  $\rm B$  the Dirac weights are  $1/(1+0.5^2) = 0.8$  $($for  $\tau = 0)$  and  $0.2$  $($for  $\tau = 1 \ \rm µ s)$.

• According to the  basic laws  of statistics, the non-central first and second order moments are:

$$m_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0 + 0.2 \cdot 1\,{\rm µ s} = 0.2\,{\rm µ s} \hspace{0.05cm},\hspace{0.5cm} m_{\rm 2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0^2 + 0.2 \cdot (1\,{\rm µ s})^2 = 0.2\,({\rm µ s})^2 \hspace{0.05cm}.$$

• To get the result you are looking for you can use the  Steiner's Theorem:

$$\sigma_{\rm V}^2 = m_{\rm 2} - m_{\rm 1}^2 = 0.2\,({\rm µ s})^2 - (0.2\,{\rm µ s})^2 = 0.16\,({\rm µ s})^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {= 0.4\,{\rm µ s}}\hspace{0.05cm}.$$

(4)  The frequency correlation function is the Fourier transform of  ${\it \Phi}_{\rm V}(\tau) = \delta(\tau) + \delta(\tau \, – \tau_0)$:

$$\varphi_{\rm F}(\Delta f) = 1 + {\rm exp}(-{\rm j} \cdot 2\pi \cdot \Delta f \cdot \tau_0) = 1 + {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0) $$

Frequency correlation function and coherence bandwidth

$$\Rightarrow \hspace{0.3cm} |\varphi_{\rm F}(\Delta f)| = \sqrt{2 + 2 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.05cm}.$$

• The maximum at  $\Delta f = 0$  is equal to  $2$.
• Therefore the equation to determine $B_{\rm K}$ is

$$|\varphi_{\rm F}(B_{\rm K})| = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(B_{\rm K})|^2 = 1 $$

$$ \Rightarrow \hspace{0.3cm}2 + 2 \cdot {\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = -0.5 \hspace{0.3cm} $$

$$\Rightarrow \hspace{0.3cm}2\pi \cdot B_{\rm K} \cdot \tau_0 = \frac{2\pi}{3}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}B_{\rm K} = \frac{1}{3\tau_0} = 333\,{\rm kHz}\hspace{0.05cm}.$$

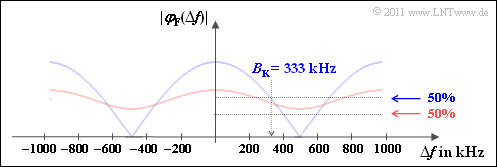
Solution 1 is correct.  The graph (blue curve) illustrates the result.

(5)  For channel  ${\rm B}$  the corresponding equations are

$${\it \Phi}_{\rm V}(\tau) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1^2 \cdot \delta(\tau) + (-0.5)^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm},\hspace{0.05cm}$$

$$\varphi_{\rm F}(\Delta f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + 0.25 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot 0.25 \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0)\hspace{0.05cm},$$

$$|\varphi_{\rm F}(\Delta f)| \hspace{-0.1cm} \ = \ \sqrt{\frac{17}{16} + \frac{1}{2} \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.3cm}$$

$$\Rightarrow \hspace{0.3cm}{\rm Max}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 1.25\hspace{0.05cm},\hspace{0.2cm}{\rm Min}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 0.75\hspace{0.05cm}.$$

You can see from this result that the  $50\%$–coherence bandwidth cannot be specified here   ⇒   solution 4 is correct.

This result is the reason why there are different definitions for the coherence range in the literature, for example

• the  $90\%$–coherence bandwidth  $($in the example  $B_{\rm K, \hspace{0.03cm} 90\%} =184 \ \ \rm kHz$$)$,
• the very simple approximation  $B_{\rm K}\hspace{0.01cm}'$  given above  $($in the example  $B_{\rm K}\hspace{0.01cm}' =1 \ \ \rm MHz)$.

You can see from these numerical values that all the information on this topic is very vague and that the individual „coherence bandwidths” can be very different.