Difference between revisions of "Aufgaben:Exercise 2.8: Huffman Application for a Markov Source"
| (41 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Entropy_Coding_According_to_Huffman |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_A_2_8.png|right|frame|Binary symmetric Markov source]] |
| − | + | We consider the symmetric Markov source according to the graph, which is completely given by the single parameter | |
:$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = | :$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = | ||
| − | {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y})$$ | + | {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}).$$ |
| − | |||
| − | + | *The given source symbol sequences apply to the conditional probabilities $q = 0.2$ and $q = 0.8$, respectively. | |
| + | *In subtask '''(1)''' it has to be clarified which symbol sequence – the red or the blue one – was generated with $q = 0.2$ and which with $q = 0.8$ . | ||
| − | |||
| − | |||
| − | :* | + | The properties of Markov sources are described in detail in the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. Due to the symmetry assumed here with regard to the binary symbols $\rm X$ and $\rm Y$, some serious simplifications result, as is derived in [[Aufgaben:1.5Z_Symmetrische_Markovquelle|Exercise 1.5Z]]: |
| − | :$$H = q \cdot {\rm | + | * The symbols $\rm X$ and $\rm Y$ are equally probable, that is, $p_{\rm X} = p_{\rm Y} = 0.5$ holds. <br>Thus the first entropy approximation is $H_1 = 1\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}. $ |
| − | = 0.722\,\,{\rm bit/ | + | * The entropy of the Markov source for $q = 0.2$ as well as for $q = 0.8$ results in |
| − | \hspace{0.05cm}.$$ | + | :$$H = q \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{q} + (1-q) \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{1-q} |
| − | + | = 0.722\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$ | |
| + | * For Markov sources, all entropy approximations $H_k$ with order $k \ge 2$ are determined by $H_1$ and $H = H_{k \to \infty}$: | ||
| + | :$$H_k = {1}/{k}\cdot \big [ H_1 + H \big ] \hspace{0.05cm}.$$ | ||
| + | *The following numerical values again apply equally to $q = 0.2$ and $q = 0.8$ : | ||
| + | :$$H_2 = {1}/{2}\cdot \big [ H_1 + H \big ] = 0.861\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm},$$ | ||
| + | :$$H_3 = {1}/{3} \cdot \big [ H_1 + 2H \big ] = 0.815\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$ | ||
| − | + | In this exercise, the Huffman algorithm is to be applied to $k$–tuples, where we restrict ourselves to $k = 2$ and $k = 3$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | <u>Hints:</u> |
| + | *The exercise belongs to the chapter [[Information_Theory/Entropiecodierung_nach_Huffman|Entropy Coding according to Huffman]]. | ||
| + | *In particular, reference is made to the page [[Information_Theory/Entropiecodierung_nach_Huffman#Application_of_Huffman_coding_to_.7F.27.22.60UNIQ-MathJax168-QINU.60.22.27.7F.E2.80.93tuples|Application of Huffman coding to $k$-tuples]]. | ||
| + | *Useful information can also be found in the specification sheets for [[Aufgaben:Exercise_2.7:_Huffman_Application_for_Binary_Two-Tuples|Exercise 2.7]] and [[Aufgaben:Exercise_2.7Z:_Huffman_Coding_for_Two-Tuples_of_a_Ternary_Source|Exercise 2.7Z]]. | ||
| + | *To check your results, please refer to the (German language) SWF module [[Applets:Huffman_Shannon_Fano|Coding according to Huffman and Shannon/Fano]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the example sequences given at the front is true for $q = 0.8$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - The red source symbol sequence '''1''', |
| − | + | + | + the blue source symbol sequence '''2'''. |
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The direct application of Huffman is also useful here. |
| − | + Huffman | + | + Huffman makes sense when forming two-tuples $(k = 2)$. |
| − | + Huffman | + | + Huffman makes sense when forming tuples of three $(k = 3)$. |
| − | { | + | {What are the probabilities of <u>two-tuples</u> $(k = 2)$ for $\underline{q = 0.8}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_{\rm A} = \rm Pr(XX)\ = \ $ { 0.4 3% } |
| − | $ | + | $p_{\rm B} = \rm Pr(XY)\ = \ $ { 0.1 3% } |
| − | $ | + | $p_{\rm C} = \rm Pr(YX)\ = \ $ { 0.1 3% } |
| − | $ | + | $p_{\rm D} = \rm Pr(YY)\ = \ $ { 0.4 3% } |
| − | { | + | {Find the Huffman code for $\underline{k = 2}$. What is the average code word length in this case? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_{\rm M} \ = \ $ { 0.9 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | { | + | {What is the bound on the average code word length when <u>two-tuples</u> are formed $(k = 2)$? Interpretation. |
| − | |type=" | + | |type="()"} |
| − | - | + | - $L_{\rm M} \ge H_1 = 1.000$ $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | + | + | + $L_{\rm M} \ge H_2 \approx 0.861$ $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | - | + | - $L_{\rm M} \ge H_3 \approx 0.815$ $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | - | + | - $L_{\rm M} \ge H_{k \to \infty} \approx 0.722$ $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | - | + | - $L_{\rm M} \ge 0.5$ $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | { | + | {Calculate the probabilities of the <u>three-tuple</u> $(k = 3)$ for $\underline{q = 0.8}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_{\rm A} = \rm Pr(XXX)\ = \ $ { 0.32 3% } |
| − | $ | + | $p_{\rm B} = \rm Pr(XXY)\ = \ $ { 0.08 3% } |
| − | $ | + | $p_{\rm C} = \rm Pr(XYX)\ = \ $ { 0.02 3% } |
| − | $ | + | $p_{\rm D} = \rm Pr(XYY)\ = \ $ { 0.08 3% } |
| − | $ | + | $p_{\rm E} = \rm Pr(YXX)\ = \ $ { 0.08 3% } |
| − | $ | + | $p_{\rm F} = \rm Pr(YXY)\ = \ $ { 0.02 3% } |
| − | $ | + | $p_{\rm G} = \rm Pr(YYX)\ = \ $ { 0.08 3% } |
| − | $ | + | $p_{\rm H} = \rm Pr(YYY)\ = \ $ { 0.32 3% } |
| − | { | + | {Find the Huffman code for $\underline{k = 3}$. What is the average code word length in this case? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_{\rm M} \ = \ $ { 0.84 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
| Line 89: | Line 96: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | < | + | '''(1)''' Correct is the <u>solution suggestion 2</u>: |
| − | + | *In the blue source symbol sequence '''2''' one recognizes much less symbol changes than in the red sequence. | |
| − | {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$$ | + | *The symbol sequence '''2''' was generated with the parameter $q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = |
| − | + | {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$ and the red symbol sequence '''1''' with $q = 0.2$. | |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Answers 2 and 3</u> are correct: | ||
| + | *Since here the source symbols $\rm X$ and $\rm Y$ were assumed to be equally probable, the direct application of Huffman makes no sense. | ||
| + | *In contrast, one can use the inner statistical depenndecies of the Markov source for data compression if one forms $k$–tuples $(k ≥ 2)$. | ||
| + | *The larger $k$ is, the more the average code word length $L_{\rm M}$ approaches the entropy $H$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The symbol probabilities are $p_{\rm X} = p_{\rm Y} = 0.5$, which gives us for the two-tuples: | ||
| + | :$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XX}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot q = 0.5 \cdot 0.8 \hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm},$$ | ||
| + | :$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XY}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$ | ||
| + | :$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YX}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$ | ||
| + | :$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YY}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot q = 0.5 \cdot 0.8\hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | [[File:P_ID2462__Inf_A_2_8d.png|right|frame|For Huffman coding for $k = 2$]] | ||
| + | '''(4)''' Opposite screen capture of the (earlier) SWF applet [[Applets:Huffman_Shannon_Fano|Coding according to Huffman and Shannon/Fano]] shows the construction of the Huffman code for $k = 2$ with the probabilities just calculated. | ||
| + | *Thus, the average code word length is: | ||
| + | :$$L_{\rm M}\hspace{0.01cm}' = 0.4 \cdot 1 + 0.4 \cdot 2 + (0.1 + 0.1) \cdot 3 = 1.8\,\,\text { bit/two-tuple}$$ | ||
| + | :$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.9\,\text{ bit/source symbol}}\hspace{0.05cm}.$$ | ||
| + | |||
| − | < | + | '''(5)''' Correct is the <u>suggested solution 2</u>: |
| + | *According to the source coding theorem $L_{\rm M} ≥ H$ holds. | ||
| + | *However, if we apply Huffman coding and disregard ties between non-adjacent symbols $(k = 2)$, the lower bound of the code word length is not $H = 0.722$, but $H_2 = 0.861$ (the addition "bit/source symbol" is omitted for the rest of the task). | ||
| + | *The result of subtask '''(4)''' was $L_{\rm M} = 0.9.$ | ||
| + | *If an asymmetrical Markov chain were present and in such a way that for the probabilities $p_{\rm A}$, ... , $p_{\rm D}$ the values $50\%$, $25\%$ and twice $12.5\%$ would result, then one would come to the average code word length $L_{\rm M} = 0.875$. | ||
| + | *How the exact parameters of this asymmetrical Markov source look, however, is not known even to the task creator (G. Söder). | ||
| + | *Nor how the value $0.875$ could be reduced to $0.861$. In any case, the Huffman algorithm is unsuitable for this. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' With $q = 0.8$ and $1 - q = 0.2$ we get: | |
| − | :$$ | + | :$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXX}) = 0.5 \cdot q^2 \hspace{0.15cm}\underline{ = 0.32} = p_{\rm H} = {\rm Pr}(\boldsymbol{\rm YYY})\hspace{0.05cm},$$ |
| − | \hspace{0.2cm} = 1. | + | :$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXY}) = 0.5 \cdot q \cdot (1-q) \hspace{0.15cm}\underline{ = 0.08}= p_{\rm G} = {\rm Pr}(\boldsymbol{\rm YYX}) \hspace{0.05cm},$$ |
| − | :$$\ | + | :$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYX}) = 0.5 \cdot (1-q)^2\hspace{0.15cm}\underline{ = 0.02} = p_{\rm F}= {\rm Pr}(\boldsymbol{\rm YXY}) \hspace{0.05cm},$$ |
| + | :$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYY}) = 0.5 \cdot (1-q) \cdot q \hspace{0.15cm}\underline{ = 0.08} = p_{\rm E} = {\rm Pr}(\boldsymbol{\rm YXX})\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | [[File:P_ID2463__Inf_A_2_8g.png|right|frame|On the Huffman coding for $k = 3$]] | |
| + | '''(7)''' The screen capture of the of the (earlier) SWF applet [[Applets:Huffman_Shannon_Fano|Coding according to Huffman and Shannon/Fano]] coding illustrates the constellation of the Huffman code for $k = 3$. | ||
| − | + | This gives us for the average code word length: | |
| − | :$$ | + | :$$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 2 + 0.24 \cdot 3 + 0.04 \cdot 5 = 2.52\,\,{\rm bit/three tupel}$$ |
| − | + | :$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{3}\hspace{0.15cm}\underline{ = 0.84\,{\rm bit/source\:symbol}}\hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | + | *One can see the improvement over subtask '''(4)'''. | |
| − | + | *The bound $k = 2$ valid for $H_2 = 0.861$ is now undercut by the average code word length $L_{\rm M}$. | |
| − | + | *The new bound for $k = 3$ is $H_3 = 0.815$. | |
| − | + | *However, to reach the source entropy $H = 0.722$ (or better: to come close to this final value up to an $ε$ ), one would have to form infinitely long tuples $(k → ∞)$. | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 130: | Line 158: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^2.3 Entropy Coding according to Huffman^]] |
Latest revision as of 17:04, 1 November 2022
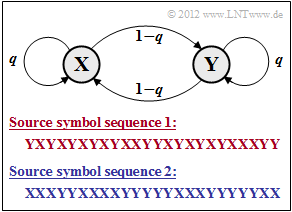
We consider the symmetric Markov source according to the graph, which is completely given by the single parameter
- $$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}).$$
- The given source symbol sequences apply to the conditional probabilities $q = 0.2$ and $q = 0.8$, respectively.
- In subtask (1) it has to be clarified which symbol sequence – the red or the blue one – was generated with $q = 0.2$ and which with $q = 0.8$ .
The properties of Markov sources are described in detail in the chapter Discrete Sources with Memory. Due to the symmetry assumed here with regard to the binary symbols $\rm X$ and $\rm Y$, some serious simplifications result, as is derived in Exercise 1.5Z:
- The symbols $\rm X$ and $\rm Y$ are equally probable, that is, $p_{\rm X} = p_{\rm Y} = 0.5$ holds.
Thus the first entropy approximation is $H_1 = 1\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}. $ - The entropy of the Markov source for $q = 0.2$ as well as for $q = 0.8$ results in
- $$H = q \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{q} + (1-q) \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{1-q} = 0.722\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$
- For Markov sources, all entropy approximations $H_k$ with order $k \ge 2$ are determined by $H_1$ and $H = H_{k \to \infty}$:
- $$H_k = {1}/{k}\cdot \big [ H_1 + H \big ] \hspace{0.05cm}.$$
- The following numerical values again apply equally to $q = 0.2$ and $q = 0.8$ :
- $$H_2 = {1}/{2}\cdot \big [ H_1 + H \big ] = 0.861\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm},$$
- $$H_3 = {1}/{3} \cdot \big [ H_1 + 2H \big ] = 0.815\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$
In this exercise, the Huffman algorithm is to be applied to $k$–tuples, where we restrict ourselves to $k = 2$ and $k = 3$.
Hints:
- The exercise belongs to the chapter Entropy Coding according to Huffman.
- In particular, reference is made to the page Application of Huffman coding to $k$-tuples.
- Useful information can also be found in the specification sheets for Exercise 2.7 and Exercise 2.7Z.
- To check your results, please refer to the (German language) SWF module Coding according to Huffman and Shannon/Fano.
Questions
Solution
- In the blue source symbol sequence 2 one recognizes much less symbol changes than in the red sequence.
- The symbol sequence 2 was generated with the parameter $q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$ and the red symbol sequence 1 with $q = 0.2$.
(2) Answers 2 and 3 are correct:
- Since here the source symbols $\rm X$ and $\rm Y$ were assumed to be equally probable, the direct application of Huffman makes no sense.
- In contrast, one can use the inner statistical depenndecies of the Markov source for data compression if one forms $k$–tuples $(k ≥ 2)$.
- The larger $k$ is, the more the average code word length $L_{\rm M}$ approaches the entropy $H$.
(3) The symbol probabilities are $p_{\rm X} = p_{\rm Y} = 0.5$, which gives us for the two-tuples:
- $$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XX}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot q = 0.5 \cdot 0.8 \hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm},$$
- $$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XY}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$
- $$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YX}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$
- $$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YY}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot q = 0.5 \cdot 0.8\hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm}.$$
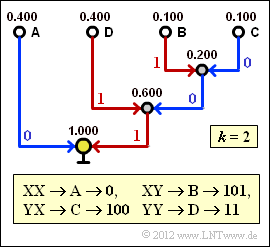
(4) Opposite screen capture of the (earlier) SWF applet Coding according to Huffman and Shannon/Fano shows the construction of the Huffman code for $k = 2$ with the probabilities just calculated.
- Thus, the average code word length is:
- $$L_{\rm M}\hspace{0.01cm}' = 0.4 \cdot 1 + 0.4 \cdot 2 + (0.1 + 0.1) \cdot 3 = 1.8\,\,\text { bit/two-tuple}$$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.9\,\text{ bit/source symbol}}\hspace{0.05cm}.$$
(5) Correct is the suggested solution 2:
- According to the source coding theorem $L_{\rm M} ≥ H$ holds.
- However, if we apply Huffman coding and disregard ties between non-adjacent symbols $(k = 2)$, the lower bound of the code word length is not $H = 0.722$, but $H_2 = 0.861$ (the addition "bit/source symbol" is omitted for the rest of the task).
- The result of subtask (4) was $L_{\rm M} = 0.9.$
- If an asymmetrical Markov chain were present and in such a way that for the probabilities $p_{\rm A}$, ... , $p_{\rm D}$ the values $50\%$, $25\%$ and twice $12.5\%$ would result, then one would come to the average code word length $L_{\rm M} = 0.875$.
- How the exact parameters of this asymmetrical Markov source look, however, is not known even to the task creator (G. Söder).
- Nor how the value $0.875$ could be reduced to $0.861$. In any case, the Huffman algorithm is unsuitable for this.
(6) With $q = 0.8$ and $1 - q = 0.2$ we get:
- $$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXX}) = 0.5 \cdot q^2 \hspace{0.15cm}\underline{ = 0.32} = p_{\rm H} = {\rm Pr}(\boldsymbol{\rm YYY})\hspace{0.05cm},$$
- $$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXY}) = 0.5 \cdot q \cdot (1-q) \hspace{0.15cm}\underline{ = 0.08}= p_{\rm G} = {\rm Pr}(\boldsymbol{\rm YYX}) \hspace{0.05cm},$$
- $$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYX}) = 0.5 \cdot (1-q)^2\hspace{0.15cm}\underline{ = 0.02} = p_{\rm F}= {\rm Pr}(\boldsymbol{\rm YXY}) \hspace{0.05cm},$$
- $$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYY}) = 0.5 \cdot (1-q) \cdot q \hspace{0.15cm}\underline{ = 0.08} = p_{\rm E} = {\rm Pr}(\boldsymbol{\rm YXX})\hspace{0.05cm}.$$
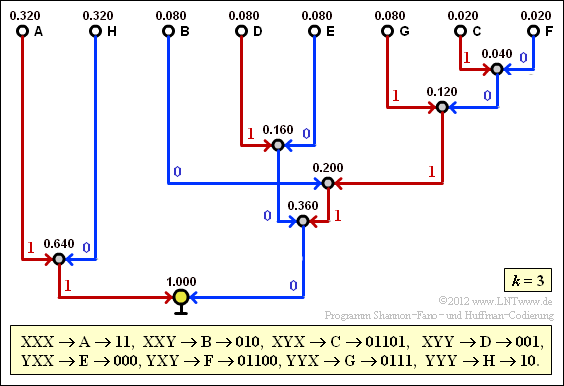
(7) The screen capture of the of the (earlier) SWF applet Coding according to Huffman and Shannon/Fano coding illustrates the constellation of the Huffman code for $k = 3$.
This gives us for the average code word length:
- $$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 2 + 0.24 \cdot 3 + 0.04 \cdot 5 = 2.52\,\,{\rm bit/three tupel}$$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{3}\hspace{0.15cm}\underline{ = 0.84\,{\rm bit/source\:symbol}}\hspace{0.05cm}.$$
- One can see the improvement over subtask (4).
- The bound $k = 2$ valid for $H_2 = 0.861$ is now undercut by the average code word length $L_{\rm M}$.
- The new bound for $k = 3$ is $H_3 = 0.815$.
- However, to reach the source entropy $H = 0.722$ (or better: to come close to this final value up to an $ε$ ), one would have to form infinitely long tuples $(k → ∞)$.