Exercise 3.10: Rayleigh Fading

Rayleigh WDF

One often describes a bandpass transmission system in the so-called equivalent lowpass domain. This representation leads according to the chapter "Bandpass-like signals" in the book Signal Representation to a complex signal:

$$z(t)=x(t)+ {\rm j} \cdot y(t).$$

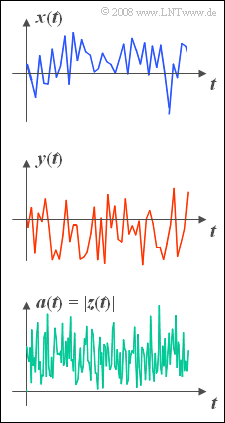
The real part $x(t)$ denotes the inphase component and the imaginary part $y(t)$ the quadrature component.

In a mobile radio system where there is no line of sight between the mobile user and the base station, the radio signal thus reaches the receiver exclusively by indirect means (refraction, scattering, reflection, etc.);

In this case, the following model is applicable:

The real part $x(t)$ and also the imaginary part $y(t)$ are both distributed and zero mean.
$x(t)$ and $y(t)$ each have the same dispersion $\sigma$ and are independent of each other.
Internal binding of the signals $x(t)$ and $y(t)$ due to the Doppler effect shall not be considered here.

The complex signal $z(t)$ can also be represented by magnitude and phase:

$$ z(t)= a(t)\cdot {\rm e}^{\rm j} \phi(t)}.$$

Because of symmetry with respect to $x(t)$ and $y(t)$ the phase $\phi(t)$ is uniformly distributed.
In contrast, the magnitude $a(t) = |z(t)|$ is Rayleigh distributed, which has led to the naming "Rayleigh fading".
As a further quantity we define the instantaneous power

$$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$

The random variable $p$ here (one-sided) exponentially distributed. Its PDF is for $p>0$:

$$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$

For all negative $p$–values, of course $f_p(p)= 0$ holds, since $p$ denotes a power.

Hints:

This exercise belongs to the chapter Further Distributions.
In particular, reference is made to the page Rayleigh PDF.
The rms of the two Gaussian random variables $x$ and $y$ are each $\sigma = 1$.
All variables are therefore to be understood as normalized.

Questions

	Small instantaneous powers are more likely than large ones.
	The phase $\phi(t) = \pi/2$ also means "Imaginärteil $y(t) = 0$".
	The phase $\phi(t) = -\pi/2$ also means "real part $x(t) = 0$".

${\rm Pr}(p(t) > 4) \ = \ $

$\ \%$

${\rm Pr}(a(t) > 2) \ = \ $

$\ \%$

$f_a(a = 1)\ = \ $

Musterlösung

Solution

(1) Richtig sind der erste und der dritte Lösungsvorschlag:

Die erste Aussage trifft aufgrund der Exponentialverteilung für $p(t)$ zu.
Ein Phasenwinkel $\phi(t) = \pm \pi/2 \ (\pm 90^\circ)$ bedeutet, dass der Realteil $x(t) = 0$ ist.
Bei positivem Imaginärteil ⇒ $y(t) > 0$ ist der Phasenwinkel $\phi(t) = +90^\circ$, bei negativem Imaginärteil beträgt der Phasenwinkel $\phi(t) = -90^\circ$.

(2) Mit $\sigma = 1$ gilt für die WDF der Momentanleistung:

$$f_p(p)= {\rm 1}/{\rm 2}\cdot{\rm e}^{-p/\rm 2}.$$

Die gesuchte Wahrscheinlichkeit ist demnach:

$${\rm Pr}(p(t) > 4) = \int_{\rm 4}^{\infty}{1}/{2}\cdot{\rm e}^{-p/\rm 2}\,{\rm d} p={\rm e}^{\rm -2} \rm \hspace{0.15cm}\underline{=13.5\%}.$$

(3) Da $p(t) =a^2(t)$ gilt und zudem $a(t) < 0$ nicht möglich ist, ist das Ereignis $a(t) > 2$ identisch mit dem Ereignis $p(t) > 4$:

Es ergibt sich die gleiche Wahrscheinlichkeit ${\rm Pr}(a(t) > 2) \hspace{0.15cm}\underline{=13.5\%}$ wie unter (2) berechnet.

(4) Allgemein gilt:

$$f_a(a)=\frac{f_p(p)}{|g'(p)|}\Bigg |_{\, p=h(a)}.$$

Die Transformationskennlinie lautet:

$$g\hspace{0.05cm}'(p)=\frac{ {\rm d} a}{ {\rm d} p}=\frac{1}{2 \cdot \sqrt{p}}.$$

Diese ist stets positiv. Daraus folgt für die Rayleigh–WDF:

$$f_a(a)=\sqrt {p}\cdot {\rm e}^{ -p/\rm 2}\Big|_{ p=a^{\rm 2}}= a\cdot {\rm e}^{\, -a^{\rm 2}/\rm 2}.$$

Für $a = 1$ ergibt sich somit der Wert $f_a(a = 1)= {\rm e}^{-0.5}\hspace{0.15cm}\underline{=0.607} $.