Difference between revisions of "Aufgaben:Exercise 3.11: Viterbi Path Finding"
| Line 83: | Line 83: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
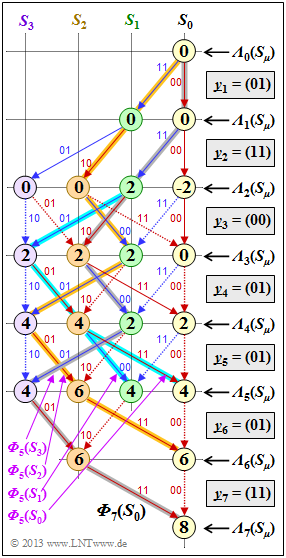
| − | '''(1)''' Correct is the <u>proposed solution 2</u>: | + | '''(1)''' Correct is the <u>proposed solution 2</u>: |
| − | *Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$. | + | *Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$. |
| − | *Using the | + | |
| + | *Using the 2-bit sequences $(00, \, 01, \, 10$ or $11)$ given at the transitions, we obtain in the forward direction the result according to <u>proposition 2</u>: | ||
:$$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$ | :$$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$ | ||
| − | * | + | *One not reach the final node ${\it \Lambda}_7(S_0)$ along other paths. |
| − | '''(2)''' By comparing the | + | '''(2)''' By comparing the decoder sequence $\underline{z}$ selected in subtask '''(1)''' with the received sequence |
| − | :$$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big )$$ | + | :$$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ),$$ |
| − | one detects <u>three bit errors</u> at positions 2, 5, and 8. | + | one detects <u>three bit errors</u> at positions '''2''', '''5''', and '''8'''. |
| − | *If a | + | |
| − | *Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see [[Aufgaben:Exercise_3.10:_Metric_Calculation| | + | *If a encoded sequence $\underline{x} ≠ \underline{z}$ was sent, there can of course be more. |
| + | |||
| + | *Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see [[Aufgaben:Exercise_3.10:_Metric_Calculation|$\text{Exercise 3.10}$]] – but one can assume that a correct decision ⇒ $\underline{z} = \underline{x}$ has been made. | ||
[[File:P_ID2697__KC_A_3_11_ML_neu.png|right|frame|Viterbi path finding]] | [[File:P_ID2697__KC_A_3_11_ML_neu.png|right|frame|Viterbi path finding]] | ||
| − | '''(3)''' Correct is <u>proposed solution 1</u>: | + | '''(3)''' Correct is the <u>proposed solution 1</u>: |
| − | *From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of <u>solution proposal 1</u>: red – blue – red – blue – blue – red – red. | + | *From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of <u>solution proposal 1</u>: red – blue – red – blue – blue – red – red. |
| − | *It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. | + | |
| − | + | *It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. Only by termination one arrives at the total length $L' = L + m = 7$. | |
| − | '''(4)''' At time $i = 6$ there are still two surviving paths. A decision could be forcibly made based on the larger metric. | + | '''(4)''' At time $i = 6$ there are still two surviving paths. |
| + | *A decision could be forcibly made based on the larger metric. | ||
| + | *However, because of ${\it \Lambda}_6(S_0) = {\it \Lambda}_6(S_2) = 6$ this is not possible in our example ⇒ <u>No</u>. | ||
| − | |||
| + | '''(5)''' The graph shows that <u>all proposed solutions</u> are correct. The paths are labeled ${\it \Phi}_5(S_0)$, ... , ${\it \Phi}_5(S_3)$. | ||
| − | |||
| + | '''(6)''' The constraint decision at time $i = 5$ would select the path with the largest metric ${\it \Lambda}_5(S_{\mu})$, <br>i.e., the path ${\it \Phi}_5(S_2)$ corresponding to <u>proposition 3</u>. | ||
| − | '''(7)''' Based on our solution to subtask (1), the path ${\it \Phi}_5(S_3)$ according to <u>proposition 4</u> would have been the better choice. | + | |
| − | + | '''(7)''' Based on our solution to subtask '''(1)''', the path ${\it \Phi}_5(S_3)$ according to <u>proposition 4</u> would have been the better choice. This is part of the path to ${\it \Phi}_7(S_0)$. | |
| − | *At | + | |
| − | *The (ultimately correct) path is only highlighted by the two termination bits. | + | *At time $i = 5$, however, there is still nothing in favor of this choice. |
| + | |||
| + | *The (ultimately correct) path is only highlighted by the two termination bits. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:06, 19 November 2022
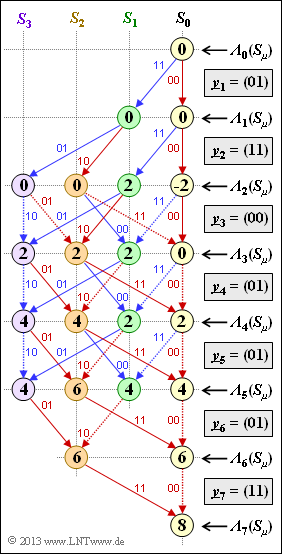
One result of $\text{Exercise 3.10}$ was adjacent trellis evaluation in terms of metrics ${\it \Lambda}_i(S_{\mu})$.
- At all decoding steps $i$ the $($in general$)$ $2^m = 4$ metrics were determined, selecting for each node the larger of two comparison values.
- The branch with the lower value was discarded. One can recognize discarded branches in the graph by dotted lines.
Otherwise, the same conditions apply as for $\text{Exercise 3.10}$. For example, also in the adjacent graph, a red arrow indicates the information bit $u_i = 0$ and a blue arrow stands for $u_i = 1$.
In the present exercise we consider the second and important part of the Viterbi algorithm, namely the search for the "surviving paths" ${\it \Phi}_i(S_{\mu})$. These are at time $i$ in state $S_{\mu}$ with $\mu \in \{1,\ 2,\ 3,\ 4 \}$. The search is best organized in the backward direction $($i.e., from bottom to top in the graph$)$.
At the end time $($in the example $i = 7)$ there is only one surviving path ${\it \Phi}_7(S_0)$ due to termination. From this it is possible to extract:
- the sequence $\underline{z}$ selected by the decoder $($short: "decoder sequence"$)$ ⇒ highest possible probability ${\rm Pr}(\underline{z} = \underline{x})$,
- the associated information sequence $\underline{v}$ with the greatest possible probability ${\rm Pr}(\underline{v} = \underline{u})$.
A decision at an earlier time, for example at $i = 5$, does not always satisfy the maximum likelihood criterion. Here there are four surviving paths ${\it \Phi}_5(S_0), \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ {\it \Phi}_5(S_3)$, which at time $i = 5$ are in states $S_0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ S_3$.
- One of these four paths is certainly part of the maximum likelihood path, which is the best possible path for $i → ∞$ $($at termination significantly earlier, here at $i = 7)$.
- But if a constraint decision is to be made already at time $i = 5$, one usually chooses the path ${\it \Phi}_5(S_{\mu})$ with the largest metric at that time ${\it \Lambda}_5(S_{\mu})$.
Hints:
- This exercise belongs to the chapter "Decoding of Convolutional Codes".
- Reference is made in particular to the section "Evaluating the trellis in the error-free case – Path finding".
Questions
Solution
- Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$.
- Using the 2-bit sequences $(00, \, 01, \, 10$ or $11)$ given at the transitions, we obtain in the forward direction the result according to proposition 2:
- $$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$
- One not reach the final node ${\it \Lambda}_7(S_0)$ along other paths.
(2) By comparing the decoder sequence $\underline{z}$ selected in subtask (1) with the received sequence
- $$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ),$$
one detects three bit errors at positions 2, 5, and 8.
- If a encoded sequence $\underline{x} ≠ \underline{z}$ was sent, there can of course be more.
- Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see $\text{Exercise 3.10}$ – but one can assume that a correct decision ⇒ $\underline{z} = \underline{x}$ has been made.
(3) Correct is the proposed solution 1:
- From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of solution proposal 1: red – blue – red – blue – blue – red – red.
- It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. Only by termination one arrives at the total length $L' = L + m = 7$.
(4) At time $i = 6$ there are still two surviving paths.
- A decision could be forcibly made based on the larger metric.
- However, because of ${\it \Lambda}_6(S_0) = {\it \Lambda}_6(S_2) = 6$ this is not possible in our example ⇒ No.
(5) The graph shows that all proposed solutions are correct. The paths are labeled ${\it \Phi}_5(S_0)$, ... , ${\it \Phi}_5(S_3)$.
(6) The constraint decision at time $i = 5$ would select the path with the largest metric ${\it \Lambda}_5(S_{\mu})$,
i.e., the path ${\it \Phi}_5(S_2)$ corresponding to proposition 3.
(7) Based on our solution to subtask (1), the path ${\it \Phi}_5(S_3)$ according to proposition 4 would have been the better choice. This is part of the path to ${\it \Phi}_7(S_0)$.
- At time $i = 5$, however, there is still nothing in favor of this choice.
- The (ultimately correct) path is only highlighted by the two termination bits.