Difference between revisions of "Aufgaben:Exercise 3.12: Cauchy Distribution"
From LNTwww
| Line 43: | Line 43: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Theorieteil, so erkennt man, dass der Parameter $\lambda= 2$ ist. Daraus folgt (nach Integration über die WDF): | + | '''(1)''' Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Theorieteil, so erkennt man, dass der Parameter $\lambda= 2$ ist. |
| − | $$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$ | + | *Daraus folgt (nach Integration über die WDF): |
| + | :$$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$ | ||
| − | Insbesondere sind | + | *Insbesondere sind |
| − | $$F_x ( r = 2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$ | + | :$$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$ |
| − | $$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$ | + | :$$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$ |
| − | Die gesuchte Wahrscheinlichkeit ergibt sich als die Differenz zu | + | *Die gesuchte Wahrscheinlichkeit ergibt sich als die Differenz zu |
| − | $${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$ | + | :$${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$ |
| − | '''(2)''' Nach dem Ergebnis der Teilaufgabe (1) | + | '''(2)''' Nach dem Ergebnis der Teilaufgabe '''(1)''' ist $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$. |
| + | *Damit gilt für die „komplementäre” Wahrscheinlichkeit ${\rm Pr} (x > 4)= 0.148$. | ||
| + | *Die gesuchte Wahrscheinlichkeit ist aus Symmetriegründen doppelt so groß: | ||
$${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 0.296}.$$ | $${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 0.296}.$$ | ||
| + | |||
'''(3)''' <u>Alle Lösungsvorschläge</u> treffen zu: | '''(3)''' <u>Alle Lösungsvorschläge</u> treffen zu: | ||
| Line 62: | Line 66: | ||
\hspace{-0.15cm} | \hspace{-0.15cm} | ||
\frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$ | \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$ | ||
| − | *Für große $x$ liefert der Integrand den konstanten Wert $4$. Deshalb divergiert das Integral. Mit $\sigma_x \to \infty$ liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke. | + | *Für große $x$ liefert der Integrand den konstanten Wert $4$. Deshalb divergiert das Integral. |
| + | *Mit $\sigma_x \to \infty$ liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke. | ||
*„Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten. | *„Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten. | ||
| − | *Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße | + | *Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße (Beispiel: der Quotient zweier mittelwertfreier Gaußgrößen) nicht dieser Beschränkung. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:50, 12 August 2018
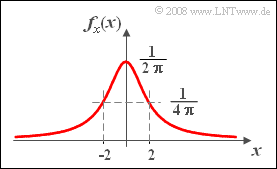
Die Wahrscheinlichkeitsdichtefunktion der Cauchyverteilung ist wie folgt gegeben:
- $$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$
Aus der Grafik ist bereits der extrem langsame Abfall des WDF–Verlaufs zu erkennen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
- Insbesondere wird auf die Seite Cauchyverteilung Bezug genommen.
Fragebogen
Musterlösung
(1) Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Theorieteil, so erkennt man, dass der Parameter $\lambda= 2$ ist.
- Daraus folgt (nach Integration über die WDF):
- $$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$
- Insbesondere sind
- $$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$
- $$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$
- Die gesuchte Wahrscheinlichkeit ergibt sich als die Differenz zu
- $${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$
(2) Nach dem Ergebnis der Teilaufgabe (1) ist $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$.
- Damit gilt für die „komplementäre” Wahrscheinlichkeit ${\rm Pr} (x > 4)= 0.148$.
- Die gesuchte Wahrscheinlichkeit ist aus Symmetriegründen doppelt so groß:
$${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 0.296}.$$
(3) Alle Lösungsvorschläge treffen zu:
- Für die Varianz der Cauchyverteilung gilt nämlich:
- $$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \hspace{-0.15cm} \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$
- Für große $x$ liefert der Integrand den konstanten Wert $4$. Deshalb divergiert das Integral.
- Mit $\sigma_x \to \infty$ liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke.
- „Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten.
- Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße (Beispiel: der Quotient zweier mittelwertfreier Gaußgrößen) nicht dieser Beschränkung.