Exercise 3.12: Cauchy Distribution
From LNTwww
The probability density function $\rm (PDF)$ of the Cauchy distribution is given as follows:
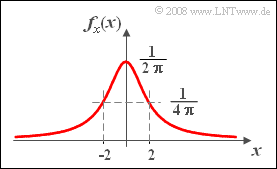
- $$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$
From the graph you can already see the extremely slow decay of the PDF course.
Hints:
- The exercise belongs to the chapter "Further Distributions".
- In particular, reference is made to the section "Cauchy PDF".
Questions
Solution
(1) Comparing the given PDF with the general equation in the theory part, we see that the parameter is $\lambda= 2$.
- From this follows (after integration over the PDF):
- $$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$
- In particular.
- $$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$
- $$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$
- The probability we are looking for is given by the difference:
- $${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$
(2) According to the result of the subtask (1) ⇒ $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$.
- Thus, for the "complementary" probability: ${\rm Pr} (x > 4)= 0.148$.
- For symmetry reasons, the probability we are looking for is twice as large:
- $${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 29.6\%}.$$
(3) All proposed solutions are true:
- For the variance of the Cauchy distribution holds namely:
- $$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \hspace{-0.15cm} \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$
- For large $x$ the integrand yields the constant value $4$. Therefore the integral diverges.
- Chebyshev's inequality does not provide an evaluable bound, even with $\sigma_x \to \infty$.
- "Natural" random variables (physically interpretable) can never be cauchy distributed, otherwise they would have an infinite power.
- On the other hand, an "artificial" (or mathematical) random variable is not subject to this restriction. Example: The quotient of two zero mean quantities.