Difference between revisions of "Aufgaben:Exercise 3.13: Path Weighting Function again"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers}} |
| − | [[File:P_ID2711__KC_A_3_13.png|right|frame| | + | [[File:P_ID2711__KC_A_3_13.png|right|frame|For the reduction of the state transition diagram]] |
| − | + | On the [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] page, for the example of our rate 1/2 standard code with memory $m = 2$ and the transfer function matrix | |
:$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$ | :$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$ | ||
| − | + | the calculation of path weighting enumerator functions was described in great detail. The results given were: | |
:$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$ | :$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$ | ||
:$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$ | :$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$ | ||
| − | + | Now the same calculations shall be done for the [[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"equivalent systematic code"]] with the transfer function matrix | |
| − | :$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 | + | :$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$ |
| − | + | can be performed. | |
| − | * | + | *The diagram shows the state transition diagram $\rm (A)$ and the structure of the reduced diagram $\rm (B)$, where the transitions are denoted by $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ in general. |
| − | *In | + | *In the subtask '''(1)''' these abbreviations are to be adapted to the state transition diagram $\rm (A)$ . |
| Line 25: | Line 25: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers| "Distance Characteristics and Error Probability Barriers"]]. |
| − | * | + | * For the solution of the subtasks '''(2)'' and '''(3)''' we refer here again to the page [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] in the theory section. |
| − | === | + | ===Solution=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What expressions do the following abbreviations stand for? |
|type="[]"} | |type="[]"} | ||
+ $A(X, \, U) = UX^2$, | + $A(X, \, U) = UX^2$, | ||
| Line 43: | Line 43: | ||
+ $G(X, \, U) = UX^2$. | + $G(X, \, U) = UX^2$. | ||
| − | { | + | {What expressions apply to the extended path weighting enumerator function? |
|type="[]"} | |type="[]"} | ||
- $T_{\rm enh}(X, \, U) = UX^5 \ / \ (1 \, –2UX)$. | - $T_{\rm enh}(X, \, U) = UX^5 \ / \ (1 \, –2UX)$. | ||
- $T_{\rm enh}(X, \, U) = UX^5 + 2 U^2X^6 + 4U^3X^7 + 8U^4X^8 + \ \text{...}$, | - $T_{\rm enh}(X, \, U) = UX^5 + 2 U^2X^6 + 4U^3X^7 + 8U^4X^8 + \ \text{...}$, | ||
| − | + | + | + None of the proposals are correct. |
| − | { | + | {What expressions apply to the "simple" path weighting enumerator function? |
|type="[]"} | |type="[]"} | ||
+ $T(X) = X^5 \ / \ (1 \, –2X)$. | + $T(X) = X^5 \ / \ (1 \, –2X)$. | ||
+ $T(X) = X^5 + 2X^6 + 4X^7 + 8X^8 + \ \text{...} $ | + $T(X) = X^5 + 2X^6 + 4X^7 + 8X^8 + \ \text{...} $ | ||
| − | - | + | - None of the proposals are correct. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u> | + | '''(1)''' <u>All proposed solutions</u> are correct. In the adapted diagram $\rm (B)$ all transitions are drawn: |
| − | [[File:P_ID2712__KC_A_3_13a.png|right|frame| | + | [[File:P_ID2712__KC_A_3_13a.png|right|frame|Reduction of the state transition diagram]] |
| − | * | + | *The transition from $S_0$ to $S_1$ is denoted by "$1 \ | \ 11$". |
| − | * | + | *The output sequence $\underline{x}_i = (11)$ is expressed by $X^2$, the input bit $u_i = 1$ by $U$. |
| − | * | + | *The same result is obtained for $G(X, \, U)$: |
:$$A(X, U) = G(X, U)= UX^2 | :$$A(X, U) = G(X, U)= UX^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The output sequences $\underline{x}_i = (01)$ as well as $\underline{x}_i = (10)$ are both marked with $X$. |
| − | * | + | *Taking into account the input bits, we thus obtain: |
:$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$ | :$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$ | ||
:$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | :$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The transition "$0 \ | \ 00$" from $S_2$ to $S_1$ is expressed by $F(X, \, U) = 1$. |
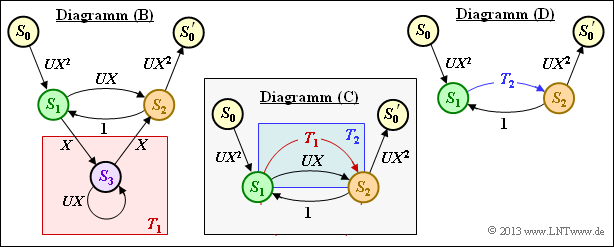
| − | '''(2)''' | + | '''(2)''' According to the procedure on page [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] in the theory section, first the transition from $S_1$ to $S_2$ via $S_3$ is summarized by an <i>ring</i>. |
| − | * | + | * One obtains for the red background in the diagram $\rm (B)$: |
:$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | :$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The two <i>parallel transitions</i> corresponding to the blue background in the diagram $\rm (C)$ can be combined as follows: |
:$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | :$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | ||
\frac{X^2 + U- U^2X^2}{1- U X} | \frac{X^2 + U- U^2X^2}{1- U X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The extended path weighting enumerator function results according to diagram $\rm (D)$ as <i>feedback</i>: |
:$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | :$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | ||
= \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | ||
| − | + | Even after several attempts, the author has not succeeded in further simplifying this expression in a target-oriented way. He tends to the <u>proposed solution 3</u> with the addition "without guarantee". | |
| − | * | + | *However, this result would imply that the extended path weighting enumerator function of the equivalent systematic code is different from that of the nonsystematic code. |
| − | * | + | *We will still clarify this issue with an expert. |
| − | '''(3)''' | + | '''(3)''' Correct are the <u>proposed solutions 1 and 2</u>: |
| − | * | + | *If one sets the formal parameter $U = 1$ in the extended function $T_{\rm enh}(X, \, U)$, one obtains the solution proposition 1: |
:$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | :$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | ||
\frac{X^5 }{1- X - X} = | \frac{X^5 }{1- X - X} = | ||
\frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | ||
| − | * | + | *Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $, we arrive at the proposed solution 2. |
| − | * | + | *That is, the simple path weighting enumerator function $T(X)$ matches for both codes. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 22:32, 20 October 2022
On the "Rules for manipulating the state transition diagram" page, for the example of our rate 1/2 standard code with memory $m = 2$ and the transfer function matrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$
the calculation of path weighting enumerator functions was described in great detail. The results given were:
- $$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$
- $$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$
Now the same calculations shall be done for the "equivalent systematic code" with the transfer function matrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$
can be performed.
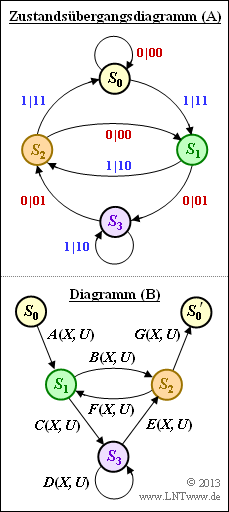
- The diagram shows the state transition diagram $\rm (A)$ and the structure of the reduced diagram $\rm (B)$, where the transitions are denoted by $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ in general.
- In the subtask (1) these abbreviations are to be adapted to the state transition diagram $\rm (A)$ .
Hints:
- This exercise belongs to the chapter "Distance Characteristics and Error Probability Barriers".
- For the solution of the subtasks (2) and (3)' we refer here again to the page "Rules for manipulating the state transition diagram" in the theory section.
Solution
Solution
- The transition from $S_0$ to $S_1$ is denoted by "$1 \ | \ 11$".
- The output sequence $\underline{x}_i = (11)$ is expressed by $X^2$, the input bit $u_i = 1$ by $U$.
- The same result is obtained for $G(X, \, U)$:
- $$A(X, U) = G(X, U)= UX^2 \hspace{0.05cm}.$$
- The output sequences $\underline{x}_i = (01)$ as well as $\underline{x}_i = (10)$ are both marked with $X$.
- Taking into account the input bits, we thus obtain:
- $$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$
- $$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X \hspace{0.05cm}.$$
- The transition "$0 \ | \ 00$" from $S_2$ to $S_1$ is expressed by $F(X, \, U) = 1$.
(2) According to the procedure on page "Rules for manipulating the state transition diagram" in the theory section, first the transition from $S_1$ to $S_2$ via $S_3$ is summarized by an ring.
- One obtains for the red background in the diagram $\rm (B)$:
- $$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} \hspace{0.05cm}.$$
- The two parallel transitions corresponding to the blue background in the diagram $\rm (C)$ can be combined as follows:
- $$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = \frac{X^2 + U- U^2X^2}{1- U X} \hspace{0.05cm}.$$
- The extended path weighting enumerator function results according to diagram $\rm (D)$ as feedback:
- $$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$
Even after several attempts, the author has not succeeded in further simplifying this expression in a target-oriented way. He tends to the proposed solution 3 with the addition "without guarantee".
- However, this result would imply that the extended path weighting enumerator function of the equivalent systematic code is different from that of the nonsystematic code.
- We will still clarify this issue with an expert.
(3) Correct are the proposed solutions 1 and 2:
- If one sets the formal parameter $U = 1$ in the extended function $T_{\rm enh}(X, \, U)$, one obtains the solution proposition 1:
- $$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= \frac{X^5 }{1- X - X} = \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$
- Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $, we arrive at the proposed solution 2.
- That is, the simple path weighting enumerator function $T(X)$ matches for both codes.