Aufgaben:Exercise 3.13: Threshold Decision vs. DFE vs. Maximum Likelihood

• Return to book

Error probabilities in comparison:
SE:    Threshold Decision,
DFE: Decision Feedback Equalization,
ML:    Maximum Likelihood Detection

Error probabilities of different receiver types are to be compared. Considered in detail are:

• Threshold Decision (SE)   ⇒   error probability  $p_{\rm SE}$,
• Decision Feedback Equalization (DFE)   ⇒   error probability  $p_{\rm DFE}$ and
• Maximum Likelihood Detection (ML)   ⇒   error probability  $p_{\rm ML}$.

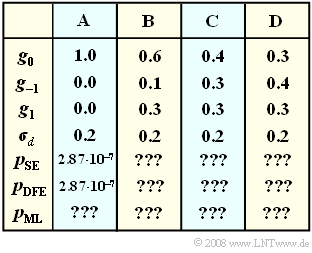
The "main value"  $g_0$, the precursor  $g_{\rm –1}$  and the postcursor  $g_1$  of the basic detection pulse, as well as the detection coefficient before the respective decision   ($\sigma_d$)  are given for four different parameter sets   $\rm A$,  $\rm B$,  $\rm C$  and  $\rm D$  in the table.

Bipolar amplitude coefficients are assumed, so that, for example, for the worst-case error probability of the receiver with single threshold decision, the following applies:

$$p_{\rm U,\hspace{0.05cm} SE } = \left\{ \begin{array}{c} {\rm Q}\big [ ({g_0-|g_{-1}|-|g_{1}|})/{\sigma_d} \big ]\\ \\{\rm Q}(0) = 0.5 \end{array} \right.\quad \begin{array}{*{1}c} {\rm with }\hspace{0.15cm}{\rm open }\hspace{0.15cm}{\rm eye }, \\ \\{\rm with }\hspace{0.15cm}{\rm closed }\hspace{0.15cm}{\rm eye }. \\ \end{array}\begin{array}{*{20}c} \\ \end{array}$$

For the Nyquist system   $\rm A$,  the mean error probability is exactly the same, viz.

$$p_{\rm SE } =p_{\rm U,\hspace{0.05cm} SE } = {\rm Q}\left( {g_0}/{\sigma_d} \right)= {\rm Q}(5) \approx 2.87 \cdot 10^{-7}\hspace{0.05cm}.$$

For the other system variants   $\rm B$,  $\rm C$  and  $\rm D$  considered here, the intersymbol interferences are so strong and the given noise rms value is so small that the following approximation can be applied:

$$p_{\rm SE } \approx {1}/{4} \cdot p_{\rm U,\hspace{0.05cm} SE } = {1}/{4} \cdot {\rm Q}\left( \frac {{\rm Max }\hspace{0.05cm}\big [0, \hspace{0.05cm}g_0-|g_{-1}|-|g_{1}|\big ]}{\sigma_d} \right)\hspace{0.05cm}.$$

Except for the Nyquist system   $\rm A$  $($here  $p_{\rm DFE} = p_{\rm SE})$,  the following approximation applies to the DFE receiver instead:

$$p_{\rm DFE } \approx {1}/{2} \cdot p_{\rm U,\hspace{0.05cm} DFE } = {1}/{2} \cdot {\rm Q}\left( \frac{{\rm Max }\hspace{0.05cm}\big [0, \hspace{0.05cm}g_0-|g_{-1}|\big ]}{\sigma_d} \right)\hspace{0.05cm}.$$

In contrast, it was shown in the  "last theory section"  for this chapter that for a receiver with ML decision, the following approximation holds:

$$p_{\rm ML } = {\rm Q}\left( \frac{{\rm Max }\hspace{0.05cm}[g_{\nu}]}{\sigma_d} \right)\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Viterbi Receiver".
• Reference is also made to the chapters  "Linear Nyquist Equalization" and "Decision Feedback".

• DYou can determine the numerical values of the Q-function using the interaction module  "Complementary Gaussian Error Functions". 
• To apply the algorithm given in the theory section for two precursors, you would have to make the following renamings (which, however, has no meaning for the calculation of the error probabilities):

$$g_{1 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{0 },\hspace{0.4cm} g_{0 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{-1 },\hspace{0.4cm} g_{-1 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{-2 } \hspace{0.05cm}.$$

Questions

1

What is the error probability for system  $\rm A$  with maximum likelihood detection (ML)?

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \cdot 10^{\rm –7} $

2

What error probabilities are to be expected with system  $\rm B$? 

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

3

What are the error probabilities for system  $\rm C$?

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

4

What error probabilities are to be expected with system  $\rm D$? 

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

Solution

Solution

(1)  Without intersymbol interference $\text{(System A)}$, the DFE and ML receivers do not improve over the simple threshold decision:

$$ p_{\rm DFE } = p_{\rm ML } = p_{\rm SE } \hspace{0.15cm}\underline {\approx 2.87 \cdot 10^{-7}} \hspace{0.05cm}.$$

(2)  With $g_0 = 0.6$, $g_{\rm –1} = 0.1$ and $g_1 = 0.3$ $\text{(System B)}$ one obtains approximately:

$$p_{\rm SE } \ \approx \ {1}/{4} \cdot {\rm Q}\left( \frac{0.6-0.1-0.3}{0.2} \right)= {1}/{4} \cdot{\rm Q}(1) \hspace{0.15cm}\underline {\approx 4\% \hspace{0.05cm}},$$

$$ p_{\rm DFE } \ \approx \ {1}/{2} \cdot {\rm Q}\left( \frac{0.6-0.1}{0.2} \right)= {1}/{2} \cdot {\rm Q}(2.5) \hspace{0.15cm}\underline {\approx 0.31\%} \hspace{0.05cm},$$

$$ p_{\rm ML } \ \approx \ {\rm Q}\left( \frac{0.6}{0.2} \right) = {\rm Q}(3) \hspace{0.15cm}\underline {\approx 0.135\%} \hspace{0.05cm}.$$

(3)  The error probabilities are with $g_0 = 0.4$ and $g_1 = g_{\rm –1} = 0.3$ $\text{(System C)}$:

$$p_{\rm SE } \ \approx \ {1}/{4} \cdot{\rm Q}(0) \hspace{0.15cm}\underline {= 12.5\%} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm closed }\hspace{0.15cm}{\rm eye } \hspace{0.05cm},$$

$$ p_{\rm DFE } \ \approx \ {1}/{2} \cdot {\rm Q}\left( \frac{0.4-0.3}{0.2} \right)= {1}/{2} \cdot {\rm Q}(0.5) \hspace{0.15cm}\underline {\approx 15\% \hspace{0.05cm}},$$

$$ p_{\rm ML } \ \approx \ {\rm Q}\left( \frac{0.4}{0.2} \right) = {\rm Q}(2) \hspace{0.15cm}\underline {\approx 2.27\%} \hspace{0.05cm}.$$

• What is interesting – and not a calculation error – is that the DFE is worse than the conventional threshold decision when the error probability is $10\%$ or more.
• See also the solution for subtask (4).

(4)  With system $\text{D}$, the DFE receiver also has a closed eye.

• The error probability $p_{\rm DFE}$ is greater than $p_{\rm SE}$, since the worst-case symbol sequence now occurs more frequently. According to the given simple approximation holds:

$$p_{\rm SE } = {1}/{4} \cdot{\rm Q}(0) = 0.125\hspace{0.05cm}, \hspace{0.2cm} p_{\rm DFE } = {1}/{2} \cdot{\rm Q}(0) \hspace{0.15cm}\underline {= 0.250} \hspace{0.05cm}.$$

• On the other hand, with an exact calculation one obtains:

$$p_{\rm SE } \ = \ {1}/{4} \cdot {\rm Q}\left( \frac{0.3-0.4-0.3}{0.2}\right) + {1}/{4} \cdot{\rm Q}\left( \frac{0.3-0.4+0.3}{0.2}\right)+ \ {1}/{4} \cdot {\rm Q}\left( \frac{0.3+0.4-0.3}{0.2}\right) +{1}/{4} \cdot{\rm Q}\left( \frac{0.3+0.4+0.3}{0.2}\right)$$

$$ \Rightarrow \hspace{0.3cm}p_{\rm SE } \ = \ {1}/{4} \cdot \left[ {\rm Q}(-2) + {\rm Q}(1) +{\rm Q}(2) +{\rm Q}(5) \right] ={1}/{4} \cdot \left[ 1+ {\rm Q}(1) +{\rm Q}(5) \right] \hspace{0.05cm}.$$

• Because of ${\rm Q}(–2) + {\rm Q}(2) = 1$ and ${\rm Q}(5) \approx 0$ we obtain $p_{\rm SE} \approx 25.5\%$.

• The same applies to the DFE receiver:

$$p_{\rm DFE } \ = \ {1}/{2} \cdot {\rm Q}\left( \frac{0.3-0.4}{0.2}\right) + {1}/{2} \cdot{\rm Q}\left( \frac{0.3+0.4}{0.2}\right)= \ {1}/{2} \cdot \left[ {\rm Q}(-0.5) + {\rm Q}(3.5) \right] \approx\frac{1- {\rm Q}(0.5)}{2}\hspace{0.15cm}\underline {= 35\%} \hspace{0.05cm}.$$

• In contrast, the error probability $p_{\rm ML}$ of a maximum likelihood receiver is still ${\rm Q}(2) \hspace{0.15cm} \underline {= 2.27\%}$.
• The sequence of the basic detection pulse values is (almost) irrelevant for the error probability of the Viterbi receiver.