Exercise 3.1: Cosine-square PDF and PDF with Dirac Functions

• Return to book

Cosine–square PDF  (top),  and
Dirac delta PDF  (bottom)

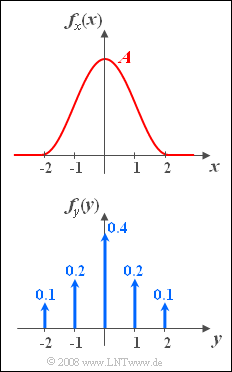
The graph shows the probability density functions  $\rm (PDF)$  of two random variables  $x$  and  $y$.

• The PDF of the random variable  $x$  in analytical form is:

$$f_x(x)=\left\{\begin{array}{*{4}{c}}A \cdot \cos^2({\pi}/{4}\cdot x) &\rm for\hspace{0.1cm} -2\le \it x\le \rm +2, \\0 & \rm else. \\\end{array}\right.$$

• The PDF of the random variable  $y$  consists of a total of five Dirac delta functions with the weights given in the graph.

If we consider these random variables as instantaneous values of two random signals  $x(t)$  and  $y(t)$,
it is obvious that both signals are  "amplitude limited"  to the range  $\pm 2$. .

Hints:

• The exercise belongs to the chapter  Probability Density Function.
• Reference is also made to the chapter  From random experiment to random variable.
• The following integral equation holds:

$$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$

Questions

1

Which of the following statements are absolutely true?

	The random variable  $x$  is continuous in value.
	The random variable $y$  is discrete in value.
	The randomness of $y$  is also discrete in time.
	The PDF says nothing regarding "discrete-time/continuous-time."

2

Calculate the parameter  $A$  of the PDF  $f_x(x)$.

$A \ = \ $

3

What is the probability that  $x = 0$  (exactly) holds?

${\rm Pr}(x = 0)\ = \ $

4

What is the probability that  $x > 0$ ?

${\rm Pr}(x > 0)\ = \ $

5

What is the probability that  $y > 0$  is?

${\rm Pr}(y > 0)\ = \ $

6

What is the probability that  $y$  is smaller than  $1$  in terms of absolute value?

${\rm Pr}(|\hspace{0.05cm}y\hspace{0.05cm}| <1)\ = \ $

7

What is the probability that  $x$  is smaller than   $1$  in terms of absolute value?

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| <1)\ = \ $

Solution

Solution

For calculating PDF area

(1)  Correct are statements 1, 2, and 4:

• $x$  is continuous value.
• $y$  is discrete value  $(M = 5)$.
• The PDF does not provide information about whether a random variable is discrete or continuous in time.

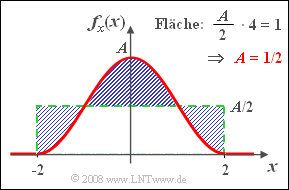
(2)  The area under the PDF must  yield $1$ .

• By simple geometric   reasoning, one arrives at the result $\underline{A=0.5}$.

(3)  The probability that the continuous-valued random variable  $x$  takes a fixed value  $x_0$  is always negligibly small   ⇒   $\underline{{\rm Pr}(x = 0) = 0}$.

• On the other hand, for the discrete value random variable  $y$  holds according to the specification:   ${\rm Pr}(y = 0) = 0.4$  $($weight of the Dirac function at  $y = 0)$.

(4)  Because of  ${{\rm Pr}(x = 0) = 0}$  and PDF symmetry, we get  $\underline{{\rm Pr}(x > 0) = 0.5}$.

(5)  Since  $y$  is a discrete random variable, the probabilities for  $y = 1$  and  $y = 2$ add up:

$${\rm Pr}(y >0) = {\rm Pr}(y = 1) + {\rm Pr}( y = 2) \hspace{0.15cm}\underline {= 0.3}.$$

(6)  The event  $|\hspace{0.05cm} y \hspace{0.05cm} | < 1$  here is identical to  $y = 0$. Thus we obtain:

$${\rm Pr}(|\hspace{0.05cm}y\hspace{0.05cm}| < 1) = {\rm Pr}( y = 0)\hspace{0.15cm}\underline { = 0.4}.$$

(7)  The probability we are looking for is equal to the integral from  $-1$  to  $+1$  over the PDF of the continuous random variable  $x$.

• Taking into account the symmetry and the given equation, we obtain:

$${\rm Pr}(|\hspace{0.05cm} x\hspace{0.05cm}|<1)=2 \cdot \int_{0}^{1}{1}/{2}\cdot \cos^2({\pi}/{4}\cdot x)\hspace{0.1cm}{\rm d}x={x}/{2}+{1}/{\pi}\cdot \sin({\pi}/{2}\cdot x)\Big |_{\rm 0}^{\rm 1}=\rm{1}/{2} + {1}/{\pi} \hspace{0.15cm}\underline{ \approx 0.818}.$$