Difference between revisions of "Aufgaben:Exercise 3.1: Phase Modulation Locus Curve"
m |
|||
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Phase_Modulation_(PM) |
}} | }} | ||
| − | [[File:P_ID1079__Mod_A_3_1.png|right|]] | + | [[File:P_ID1079__Mod_A_3_1.png|right|frame|Two locus curves to choose from]] |
| − | + | The locus curve is generally understood as the plot of the equivalent low-pass signal $s_{\rm TP}(t)$ in the complex plane. | |
| − | + | *The graph shows locus curves at the output of two modulators $\rm M_1$ and $\rm M_2$. | |
| + | *The real and imaginary parts are each normalized to $1 \ \rm V$ in this graph. | ||
| − | + | Let the source signal be the same for both modulators: | |
| − | $$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm} | + | $$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm} |
| − | + | {\rm with}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$ | |
| − | $$ s(t) = A_{\rm T} \cdot \cos \ | + | One of the two modulators implements phase modulation, which is characterized by the following equations: |
| − | $$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$ | + | :$$ s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \phi(t) \big]\hspace{0.05cm},$$ |
| − | $$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$ | + | :$$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$ |
| − | + | :$$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$ | |
| − | ''' | + | The maximum value $ϕ(t)$ is called the ''modulation index'' $η$. Often $η$ is also called ''phase deviation'' in the literature. |
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Phase_Modulation_(PM)|Phase Modulation]]. | ||
| + | *Particular reference is made to the page [[Modulation_Methods/Phase_Modulation_(PM)#Equivalent_low-pass_signal_in_phase_modulation|Equivalent low-pass signal in phase modulation]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which modulation method is used by modulator $\rm M_1$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Double-sideband amplitude modulation. |
| − | + | + | + Single sideband amplitude modulation. |
| − | - | + | - Phase modulation. |
| − | { | + | {Which modulation method is used by modulator $\rm M_2$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Double-sideband amplitude modulation. |
| − | - | + | - Single sideband amplitude modulation. |
| − | + | + | + Phase modulation. |
| − | { | + | {What is the carrier amplitude $A_{\rm T}$ for the phase modulator? Note the normalization to $1 \ \rm V$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_{\rm T} \ = \ $ { 1 3% } $\ \rm V$ |
| − | { | + | {What are the values of the modulation index $η$ and the modulator constant $K_{\rm PM}$? |
|type="{}"} | |type="{}"} | ||
| − | $η$ | + | $η\ = \ $ { 3.1415 3% } |
| − | $K_{PM}$ | + | $K_{\rm PM}\ = \ $ { 1.571 3% } $\ \rm 1/V$ |
| − | { | + | {Describe the motion on the locus curve. At what time $t_1$ is the starting point $s_{\rm TP}(t = 0) = -1 \ \rm V$ first reached again? |
|type="{}"} | |type="{}"} | ||
| − | $t_1$ | + | $t_1\ = \ $ { 100 3% } $ \ \rm µ s$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' We are dealing with SSB-AM with a sideband-to-carrier ratio $μ = 1$ ⇒ <u>Answer 2</u>: |
| + | *If one moves in the mathematically positive direction on the circle, it is specifically an USB–AM, otherwise it is a LSB–AM. | ||
| + | *The phase function $ϕ(t)$ as the angle of a point $s_{\rm TP}(t)$ on the circle (arc) with respect to the coordinate origin can take values between $±π/2$ and does not show a cosine progression. | ||
| + | *The envelope $a(t) = |s_{\rm TP}(t)|$ is also not cosine. | ||
| + | *If an envelope demodulator were used for $\rm M_1$ at the receiver, nonlinear distortions would occur, in contrast to DSB–AM, which has a horizontal straight line for a locus curve. | ||
| + | |||
| − | |||
| − | '''2 | + | '''(2)''' Here, we observe phase modulation ⇒ <u>Answer 3</u>: |
| + | *The envelope $a(t) = A_{\rm T}$ is constant, | ||
| + | *while the phase $ϕ(t)$ is cosinusoidal according to the source signal $q(t)$ . | ||
| − | |||
| − | |||
| − | |||
| − | '''4 | + | |
| − | $$ \eta = \phi_{\rm max} = \phi( t =0)\hspace{0.15cm}\underline { = | + | '''(3)''' In the case of phase modulation: |
| − | + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$ | |
| + | *From the graph, we can read the carrier amplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 1 \ \rm V}$ as the radius of the circle. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' The source signal $q(t)$ is at its maximum at time $t = 0$ and therefore so is the phase function: | ||
| + | :$$ \eta = \phi_{\rm max} = \phi( t =0) = \pi\hspace{0.15cm}\underline { = 3.1415} \hspace{0.05cm}.$$ | ||
| + | *This gives the modulator constant: | ||
$$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$ | $$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$ | ||
| − | '''5 | + | |
| + | |||
| + | |||
| + | '''(5)''' One moves clockwise along the circular arc. | ||
| + | *After a quarter of the period $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$ , $ϕ(t) = 0$ and $s_{\rm TP}(t) = 1 \, \rm V$. | ||
| + | *At time $t_1 = T_{\rm N}/2\hspace{0.15cm}\underline { = 100 \ \rm µ s}$ , $ϕ(t_1) = -π$ and $s_{\rm TP}(t_1) = -1 \, \rm V$. | ||
| + | *Afterwards, one moves counterclockwise along the arc. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 73: | Line 104: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^3.1 Phase Modulation^]] |
Latest revision as of 16:54, 9 April 2022
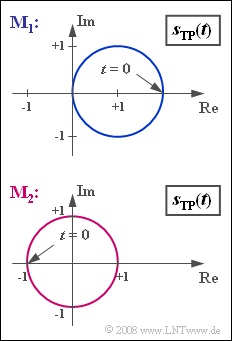
The locus curve is generally understood as the plot of the equivalent low-pass signal $s_{\rm TP}(t)$ in the complex plane.
- The graph shows locus curves at the output of two modulators $\rm M_1$ and $\rm M_2$.
- The real and imaginary parts are each normalized to $1 \ \rm V$ in this graph.
Let the source signal be the same for both modulators:
$$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm}
{\rm with}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$
One of the two modulators implements phase modulation, which is characterized by the following equations:
- $$ s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \phi(t) \big]\hspace{0.05cm},$$
- $$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$
- $$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$
The maximum value $ϕ(t)$ is called the modulation index $η$. Often $η$ is also called phase deviation in the literature.
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the page Equivalent low-pass signal in phase modulation.
Questions
Solution
- If one moves in the mathematically positive direction on the circle, it is specifically an USB–AM, otherwise it is a LSB–AM.
- The phase function $ϕ(t)$ as the angle of a point $s_{\rm TP}(t)$ on the circle (arc) with respect to the coordinate origin can take values between $±π/2$ and does not show a cosine progression.
- The envelope $a(t) = |s_{\rm TP}(t)|$ is also not cosine.
- If an envelope demodulator were used for $\rm M_1$ at the receiver, nonlinear distortions would occur, in contrast to DSB–AM, which has a horizontal straight line for a locus curve.
(2) Here, we observe phase modulation ⇒ Answer 3:
- The envelope $a(t) = A_{\rm T}$ is constant,
- while the phase $ϕ(t)$ is cosinusoidal according to the source signal $q(t)$ .
(3) In the case of phase modulation:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$
- From the graph, we can read the carrier amplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 1 \ \rm V}$ as the radius of the circle.
(4) The source signal $q(t)$ is at its maximum at time $t = 0$ and therefore so is the phase function:
- $$ \eta = \phi_{\rm max} = \phi( t =0) = \pi\hspace{0.15cm}\underline { = 3.1415} \hspace{0.05cm}.$$
- This gives the modulator constant:
$$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$
(5) One moves clockwise along the circular arc.
- After a quarter of the period $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$ , $ϕ(t) = 0$ and $s_{\rm TP}(t) = 1 \, \rm V$.
- At time $t_1 = T_{\rm N}/2\hspace{0.15cm}\underline { = 100 \ \rm µ s}$ , $ϕ(t_1) = -π$ and $s_{\rm TP}(t_1) = -1 \, \rm V$.
- Afterwards, one moves counterclockwise along the arc.