Difference between revisions of "Aufgaben:Exercise 3.1: Spectrum of the Exponential Pulse"
From LNTwww
| (4 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
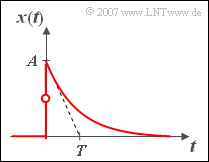
| − | [[File:P_ID494__Sig_A_3_1.png|right|frame| | + | [[File:P_ID494__Sig_A_3_1.png|right|frame|Exponential pulse]] |
In this task, a causal signal $x(t)$ is considered | In this task, a causal signal $x(t)$ is considered | ||
| − | *which rises abruptly from zero to $A$ at time $t = 0$ | + | *which rises abruptly from zero to $A$ at time $t = 0$, and |
| − | *decreases exponentially with the time constant $T$ for $t > 0$ | + | *decreases exponentially with the time constant $T$ for $t > 0$: |
:$$x(t) = A \cdot {\rm e}^{ - t/T} .$$ | :$$x(t) = A \cdot {\rm e}^{ - t/T} .$$ | ||
| − | At the | + | At the jumping point at time $t = 0$, $x(t = 0) = A/2$. |
Use the following parameters for the numerical calculations: | Use the following parameters for the numerical calculations: | ||
| Line 17: | Line 17: | ||
:$$A = 3 \hspace{0.1cm} {\rm V}, \hspace{0.4cm} T = 1 \hspace{0.1cm} {\rm ms} .$$ | :$$A = 3 \hspace{0.1cm} {\rm V}, \hspace{0.4cm} T = 1 \hspace{0.1cm} {\rm ms} .$$ | ||
| − | The spectral function $X(f)$ to be calculated will be complex and therefore can be | + | The spectral function $X(f)$ to be calculated will be complex and therefore can be represented |
*by real and imaginary part, but also | *by real and imaginary part, but also | ||
| − | *by magnitude and phase | + | *by magnitude and phase. |
| − | |||
| − | |||
| − | |||
| Line 30: | Line 27: | ||
| − | + | ''Hint:'' | |
| − | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_and_Its_Inverse|Fourier Transform and its Inverse]]. | |
| − | '' | + | *Use the notation: |
| − | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_and_Its_Inverse|Fourier Transform and | + | |
| + | :$$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi( f )} .$$ | ||
| Line 41: | Line 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the spectral function $X(f)$. What spectral value results at the frequency | + | {Calculate the spectral function $X(f)$. What spectral value results at the frequency $f = 0$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[X(f=0)] \ = \ $ { 3 3% } $\rm mV/Hz$ | $\text{Re}[X(f=0)] \ = \ $ { 3 3% } $\rm mV/Hz$ | ||
$\text{Im}[X(f=0)] \ = \ $ { 0. } $\rm mV/Hz$ | $\text{Im}[X(f=0)] \ = \ $ { 0. } $\rm mV/Hz$ | ||
| − | {What are the real and imaginary parts of $X(f)$ using $f_0 = 1/(2\pi T)$. What are the values when | + | {What are the real and imaginary parts of $X(f)$ using $f_0 = 1/(2\pi T)$. What are the values when $f = f_0$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[X(f=f_0)] \ = \ $ { 1.5 3% } $\rm mV/Hz$ | $\text{Re}[X(f=f_0)] \ = \ $ { 1.5 3% } $\rm mV/Hz$ | ||
$\text{Im}[X(f=f_0)] \ = \ $ { -1.55--1.45 } $\rm mV/Hz$ | $\text{Im}[X(f=f_0)] \ = \ $ { -1.55--1.45 } $\rm mV/Hz$ | ||
| − | {Calculate the magnitude function $|X(f)|$. Which values result at the frequency | + | {Calculate the magnitude function $|X(f)|$. Which values result at the frequency $f = f_0$ and at very high frequencies? |
|type="{}"} | |type="{}"} | ||
$|X(f=f_0)| \hspace{0.25cm} = \ $ { 2.12 3% } $\rm mV/Hz$ | $|X(f=f_0)| \hspace{0.25cm} = \ $ { 2.12 3% } $\rm mV/Hz$ | ||
$|X(f\rightarrow \infty)| \ = \ $ { 0. } $\rm mV/Hz$ | $|X(f\rightarrow \infty)| \ = \ $ { 0. } $\rm mV/Hz$ | ||
| − | {Calculate the phase function $\varphi(f)$. What values result for this at the frequency | + | {Calculate the phase function $\varphi(f)$. What values result for this at the frequency $f = f_0$ and at very high frequencies? |
|type="{}"} | |type="{}"} | ||
$\varphi(f=f_0) \hspace{0.25cm} = \ $ { 0.785 3% } $\rm rad$ | $\varphi(f=f_0) \hspace{0.25cm} = \ $ { 0.785 3% } $\rm rad$ | ||
| Line 76: | Line 74: | ||
X( {f = 0}) = A \cdot T{ = 3 \cdot 10^{ - 3}\; {\rm V/Hz}} \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}}.$$ | X( {f = 0}) = A \cdot T{ = 3 \cdot 10^{ - 3}\; {\rm V/Hz}} \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}}.$$ | ||
| − | *At the frequency | + | *At the frequency $f = 0$ , the spectrum is purely real: |
:$$\text{Re}[X(f=0)] \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}} \hspace{1.15 cm}\text{Im}[X(f=0)] \hspace{0.15 cm}\underline{ =0}.$$ | :$$\text{Re}[X(f=0)] \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}} \hspace{1.15 cm}\text{Im}[X(f=0)] \hspace{0.15 cm}\underline{ =0}.$$ | ||
| Line 83: | Line 81: | ||
'''(2)''' With the abbreviations $X_0 = A \cdot T$ and $f_0 = 1/(2\pi T)$ the spectral function is: | '''(2)''' With the abbreviations $X_0 = A \cdot T$ and $f_0 = 1/(2\pi T)$ the spectral function is: | ||
| − | |||
:$$X( f) = \frac{ {X_0 }}{ {1 +{\rm j} \cdot f/f_0 }} = \frac{ {X_0 }}{ {1 + \left( {f/f_0 } \right)^2 }} \cdot \left( {1 - {\rm j} \cdot f/f_0 } \right).$$ | :$$X( f) = \frac{ {X_0 }}{ {1 +{\rm j} \cdot f/f_0 }} = \frac{ {X_0 }}{ {1 + \left( {f/f_0 } \right)^2 }} \cdot \left( {1 - {\rm j} \cdot f/f_0 } \right).$$ | ||
Divided into real and imaginary parts, this gives: | Divided into real and imaginary parts, this gives: | ||
| − | $${\mathop{\rm Re}\nolimits} [ {X(f)}] = \frac{ {X_0 }}{{1 + \left( {f/f_0 } \right)^2 }}, | + | :$${\mathop{\rm Re}\nolimits} [ {X(f)}] = \frac{ {X_0 }}{{1 + \left( {f/f_0 } \right)^2 }}, |
\hspace{0.5 cm}{\mathop{\rm Im}\nolimits} [ {X(f)}] = - \frac{ {X_0 \cdot f/f_0 }}{ {1 + \left( {f/f_0 } \right)^2 }}.$$ | \hspace{0.5 cm}{\mathop{\rm Im}\nolimits} [ {X(f)}] = - \frac{ {X_0 \cdot f/f_0 }}{ {1 + \left( {f/f_0 } \right)^2 }}.$$ | ||
| Line 97: | Line 94: | ||
| − | |||
'''(3)''' The magnitude of a complex-valued function, which is a quotient, is equal to the quotient of the magnitudes of the numerator and denominator. | '''(3)''' The magnitude of a complex-valued function, which is a quotient, is equal to the quotient of the magnitudes of the numerator and denominator. | ||
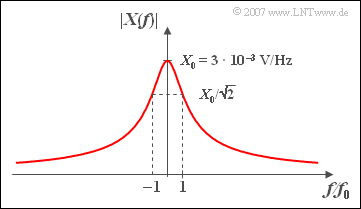
| + | [[File:P_ID548__Sig_A_3_1_c_neu.png|right|frame|Magnitude spectrum of the exponential pulse]] | ||
| + | |||
*Thus one obtains: | *Thus one obtains: | ||
| Line 105: | Line 103: | ||
:$$\Rightarrow \hspace{0.5 cm} \left| {X( {f = f_0} )} \right| = { {X_0 }}/{ {\sqrt 2 }}\hspace{0.15 cm}\underline{ = 2.12 \;{\rm mV/Hz}}.$$ | :$$\Rightarrow \hspace{0.5 cm} \left| {X( {f = f_0} )} \right| = { {X_0 }}/{ {\sqrt 2 }}\hspace{0.15 cm}\underline{ = 2.12 \;{\rm mV/Hz}}.$$ | ||
| − | *At very high frequencies $(f \rightarrow \infty)$ the magnitude is<u>almost zero</u> (see sketch). | + | *At very high frequencies $(f \rightarrow \infty)$ the magnitude is <u>almost zero</u> (see sketch). |
| Line 111: | Line 109: | ||
'''(4)''' The general rule for the phase function is: | '''(4)''' The general rule for the phase function is: | ||
| − | $$\varphi ( f ) = \arctan \left( {\frac{ { - {\mathop{\rm Im}\nolimits}[{X(f)} ]}}{{ {\mathop{\rm Re}\nolimits} [ {X(f)} ]}}} \right) = \arctan \left( {f/f_0 } \right).$$ | + | :$$\varphi ( f ) = \arctan \left( {\frac{ { - {\mathop{\rm Im}\nolimits}[{X(f)} ]}}{{ {\mathop{\rm Re}\nolimits} [ {X(f)} ]}}} \right) = \arctan \left( {f/f_0 } \right).$$ |
| − | *For $f = f_0$ this gives $\arctan(1)= \pi /4 \hspace{0.15 cm}\underline{\approx 0.785}$. | + | *For $f = f_0$ this gives $\varphi ( f_0 ) =\arctan(1)= \pi /4 \hspace{0.15 cm}\underline{\approx 0.785}$. |
| − | *For very large values of | + | *For very large values of $f$ the phase function approaches $\varphi ( f \to \infty ) =\arctan(\infty) = \pi /2 \hspace{0.15 cm}\underline{ \approx 1.571}$. |
*Both specifications are to be understood in radians. | *Both specifications are to be understood in radians. | ||
| Line 120: | Line 118: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.1 Fourier Transform and Its Inverse^]] |
Latest revision as of 15:05, 21 April 2021
In this task, a causal signal $x(t)$ is considered
- which rises abruptly from zero to $A$ at time $t = 0$, and
- decreases exponentially with the time constant $T$ for $t > 0$:
- $$x(t) = A \cdot {\rm e}^{ - t/T} .$$
At the jumping point at time $t = 0$, $x(t = 0) = A/2$.
Use the following parameters for the numerical calculations:
- $$A = 3 \hspace{0.1cm} {\rm V}, \hspace{0.4cm} T = 1 \hspace{0.1cm} {\rm ms} .$$
The spectral function $X(f)$ to be calculated will be complex and therefore can be represented
- by real and imaginary part, but also
- by magnitude and phase.
Hint:
- This exercise belongs to the chapter Fourier Transform and its Inverse.
- Use the notation:
- $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi( f )} .$$
Questions
Solution
(1) With the first Fourier integral we get:
- $$X( f ) = \int_0^\infty {A \cdot {\rm e}^{ - t\left( {1/T + {\rm j \hspace{0.05cm} \cdot \hspace{0.05cm}}2\pi f} \right)} } {\rm d}t = \left. {\frac{ { - A}}{ {1/T + {\rm j}2\pi f}} \cdot {\rm e}^{ - t\left( {1/T + {\rm j}2\pi f} \right)} } \right|_0^\infty .$$
- The upper integral limit $(t \rightarrow \infty)$ gives zero, the lower limit $(t = 0)$ gives the value $1$. Thus:
- $$X(f) = \frac{ {A \cdot T}}{ {1 + {\rm j}2\pi fT}}\hspace{0.3 cm}\Rightarrow\hspace{0.3 cm} X( {f = 0}) = A \cdot T{ = 3 \cdot 10^{ - 3}\; {\rm V/Hz}} \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}}.$$
- At the frequency $f = 0$ , the spectrum is purely real:
- $$\text{Re}[X(f=0)] \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}} \hspace{1.15 cm}\text{Im}[X(f=0)] \hspace{0.15 cm}\underline{ =0}.$$
(2) With the abbreviations $X_0 = A \cdot T$ and $f_0 = 1/(2\pi T)$ the spectral function is:
- $$X( f) = \frac{ {X_0 }}{ {1 +{\rm j} \cdot f/f_0 }} = \frac{ {X_0 }}{ {1 + \left( {f/f_0 } \right)^2 }} \cdot \left( {1 - {\rm j} \cdot f/f_0 } \right).$$
Divided into real and imaginary parts, this gives:
- $${\mathop{\rm Re}\nolimits} [ {X(f)}] = \frac{ {X_0 }}{{1 + \left( {f/f_0 } \right)^2 }}, \hspace{0.5 cm}{\mathop{\rm Im}\nolimits} [ {X(f)}] = - \frac{ {X_0 \cdot f/f_0 }}{ {1 + \left( {f/f_0 } \right)^2 }}.$$
At the frequency $f_0$
- the real part is equal to $X_0/2 \hspace{0.15 cm}\underline{ = 1.5 \; {\rm mV/Hz}},$
- the imaginary part is equal to $–X_0/2 \hspace{0.15 cm}\underline{ = \hspace{0.1 cm}-1.5 \; {\rm mV/Hz}}.$
(3) The magnitude of a complex-valued function, which is a quotient, is equal to the quotient of the magnitudes of the numerator and denominator.
- Thus one obtains:
- $$ \left| {X( f)} \right| =\frac{ {X_0 }}{ {\left| 1 +{\rm j} \cdot f/ {f_0 } \right|}} = \frac{ {X_0 }}{{\sqrt {1 + \left( {f/f_0 } \right)^2 } }},$$
- $$\Rightarrow \hspace{0.5 cm} \left| {X( {f = f_0} )} \right| = { {X_0 }}/{ {\sqrt 2 }}\hspace{0.15 cm}\underline{ = 2.12 \;{\rm mV/Hz}}.$$
- At very high frequencies $(f \rightarrow \infty)$ the magnitude is almost zero (see sketch).
(4) The general rule for the phase function is:
- $$\varphi ( f ) = \arctan \left( {\frac{ { - {\mathop{\rm Im}\nolimits}[{X(f)} ]}}{{ {\mathop{\rm Re}\nolimits} [ {X(f)} ]}}} \right) = \arctan \left( {f/f_0 } \right).$$
- For $f = f_0$ this gives $\varphi ( f_0 ) =\arctan(1)= \pi /4 \hspace{0.15 cm}\underline{\approx 0.785}$.
- For very large values of $f$ the phase function approaches $\varphi ( f \to \infty ) =\arctan(\infty) = \pi /2 \hspace{0.15 cm}\underline{ \approx 1.571}$.
- Both specifications are to be understood in radians.