Difference between revisions of "Aufgaben:Exercise 3.2Z: (3, 1, 3) Convolutional Encoder"
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Algebraic_and_Polynomial_Description}} |
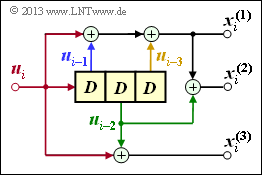
| − | [[File:P_ID2625__KC_Z_3_2_neu.png|right|frame| | + | [[File:P_ID2625__KC_Z_3_2_neu.png|right|frame|Convolutional encoder with parameters $k = 1, \ n = 3$ and $m = 3$.]] |
| − | + | The presented convolutional encoder is defined by the parameters | |
| − | *$k = 1$ $($ | + | *$k = 1$ $($only one information sequence $\underline{u})$ and |
| − | * $n = 3$ $($ | + | * $n = 3$ $($three code sequences $\underline{x}^{(1)}, \ \underline{x}^{(2)}, \ \underline{x}^{(3)})$ |
| − | + | characterized. From the number of memory cells, the memory $m = 3$. | |
| − | + | With the information bit $u_i$ to the coding step $i$ the following code bits are obtained: | |
:$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-3}\hspace{0.05cm},$$ | :$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-3}\hspace{0.05cm},$$ | ||
:$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-2} + u_{i-3} \hspace{0.05cm},$$ | :$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-2} + u_{i-3} \hspace{0.05cm},$$ | ||
:$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-2} \hspace{0.05cm}.$$ | :$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-2} \hspace{0.05cm}.$$ | ||
| − | + | From this, partial matrices $\mathbf{G}_l$ can be derived, as described on the page [[Channel_Coding/Algebraic_and_Polynomial_Description#Division_of_the_generator_matrix_into_partial_matrices|"Division of the generator matrix into partial matrices"]] . | |
| − | * | + | *For the generator matrix can thus be written: |
:$$ { \boldsymbol{\rm G}}=\begin{pmatrix} | :$$ { \boldsymbol{\rm G}}=\begin{pmatrix} | ||
{ \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | ||
| Line 25: | Line 25: | ||
\end{pmatrix}\hspace{0.05cm}.$$ | \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | * | + | *For the code sequence $\underline{x} = (x_1^{(1)}, \ x_1^{(2)}, \ x_1^{(3)}, \ x_2^{(1)}, \ x_2^{(2)}, \ x_2^{(3)}, \ \text{...})$ holds: |
:$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$ | :$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$ | ||
| Line 34: | Line 34: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Channel_Coding/Algebraic_and_Polynomial_Description| "Algebraic and Polynomial Description"]]. |
| − | * | + | *Reference is made in particular to the page [[Channel_Coding/Algebraic_and_Polynomial_Description#Division_of_the_generator_matrix_into_partial_matrices|"Division of the generator matrix into partial matrices"]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {From how many partial matrices $\mathbf{G}_l$ is the matrix $\mathbf{G}$ composed? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | ${\rm Number \ of \ partial \ matrices} \ = \ ${ 4 } |
| − | { | + | {What dimension do the partial matrices $\mathbf{G}_l$ have? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | ${\rm Rows \ of \ the \ partial \ matrices} \hspace{0.425cm} = \ ${ 1 } |
| − | ${\rm | + | ${\rm Columns \ of \ the \ partial \ matrices} \ = \ ${ 3 } |
| − | { | + | {Which statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds $\mathbf{G}_0 = (1, 1, 1)$. |
| − | + | + | + It holds $\mathbf{G}_ 1 = (1, 1, 0)$. |
| − | + | + | + It holds $\mathbf{G}_2 = (0, 1, 1)$. |
| − | + | + | + It holds $\mathbf{G}_3 = (1, 1, 0)$. |
| − | { | + | {Create the generator matrix $\mathbf{G}$ with five rows and fifteen columns. <br>What code sequence results for $\underline{u} = (1, 0, 1, 1, 0)$? |
|type="()"} | |type="()"} | ||
| − | - | + | - It holds $\underline{x} = (1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, \text{...}).$ |
| − | + | + | + It holds $\underline{x} = (1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, \text{...}).$ |
| − | - | + | - It holds $\underline{x} = (0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, \text{...}).$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the index $l$ of the partial matrices, $0 ≤ l ≤ m$. |
| − | * | + | *The coder under consideration has memory $m = 3$. |
| − | * | + | *Thereby <u>four partial matrices</u> are to be considered. |
| − | '''(2)''' | + | '''(2)''' Each partial matrix $\mathbf{G}_l$ consists of. |
| − | *<u> | + | *<u>one row</u> ⇒ $k = 1$, and |
| − | *<u> | + | *<u>three columns</u> ⇒ $n = 3$. |
| − | '''(3)''' <u> | + | '''(3)''' <u>All statements</u> are correct: |
| − | * | + | *Since the current information bit $u_i$ affects all three outputs $x_i^{(1)}, \ x_i^{(2)}$ and $x_i^{(3)}$, $\mathbf{G}_0 = (1, 1, 1)$. |
| − | * | + | *In contrast, $\mathbf{G}_3 = (1, 1, 0)$ states that only the first two inputs are affected by $u_{i-3}$, but not $x_i^{(3)}$. |
| − | '''(4)''' | + | '''(4)''' Correct is the <u>proposed solution 2</u>: |
| − | [[File:P_ID2626__KC_Z_3_2d.png|right|frame| | + | [[File:P_ID2626__KC_Z_3_2d.png|right|frame|Generator matrix $\mathbf{G}$]] |
| − | * | + | *The searched generator matrix $\mathbf{G}$ is shown on the right, where the four partial matrices $\mathbf{G}_0, \ ... , \mathbf{G}_3$ are distinguished by color. |
| − | * | + | *The following vector equation gives the result corresponding to the second proposed solution 2: |
:$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1) \cdot { \boldsymbol{\rm G}}. $$ | :$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1) \cdot { \boldsymbol{\rm G}}. $$ | ||
| − | * | + | *The code sequence $\underline{x}$ is thereby equal to the modulo 2 sum of the matrix rows 1, 3 and 4. |
| − | * | + | *The three code sequences of the individual branches are distinguished by color. For example, the following applies to the lower output: |
:$$\underline{x}^{(3)} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.$$ | :$$\underline{x}^{(3)} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.$$ | ||
| − | + | Using the equations given above, this result can be verified: | |
:$${x}_1^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 + u_{-1} = 1+ (0) = 1 \hspace{0.05cm},$$ | :$${x}_1^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 + u_{-1} = 1+ (0) = 1 \hspace{0.05cm},$$ | ||
:$${x}_2^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_2 + u_{0} = 0+ (0) = 0 \hspace{0.05cm},$$ | :$${x}_2^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_2 + u_{0} = 0+ (0) = 0 \hspace{0.05cm},$$ | ||
| Line 104: | Line 104: | ||
:$${x}_5^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_5 + u_{3} = 0+ 1 = 1 \hspace{0.05cm}.$$ | :$${x}_5^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_5 + u_{3} = 0+ 1 = 1 \hspace{0.05cm}.$$ | ||
| − | + | Notes: | |
| − | * | + | *The memory preallocation with zeros is taken into account here: $u_0 = u_{–1} = 0$. |
| − | * | + | *If, as assumed here, the information sequence is limited to four bits, then ones can occur in the code sequence up to the position $(4 + m) \cdot n = 21$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 19:46, 23 September 2022
The presented convolutional encoder is defined by the parameters
- $k = 1$ $($only one information sequence $\underline{u})$ and
- $n = 3$ $($three code sequences $\underline{x}^{(1)}, \ \underline{x}^{(2)}, \ \underline{x}^{(3)})$
characterized. From the number of memory cells, the memory $m = 3$.
With the information bit $u_i$ to the coding step $i$ the following code bits are obtained:
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-3}\hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-2} + u_{i-3} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-2} \hspace{0.05cm}.$$
From this, partial matrices $\mathbf{G}_l$ can be derived, as described on the page "Division of the generator matrix into partial matrices" .
- For the generator matrix can thus be written:
- $$ { \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm}.$$
- For the code sequence $\underline{x} = (x_1^{(1)}, \ x_1^{(2)}, \ x_1^{(3)}, \ x_2^{(1)}, \ x_2^{(2)}, \ x_2^{(3)}, \ \text{...})$ holds:
- $$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Algebraic and Polynomial Description".
- Reference is made in particular to the page "Division of the generator matrix into partial matrices".
Questions
Solution
(1) For the index $l$ of the partial matrices, $0 ≤ l ≤ m$.
- The coder under consideration has memory $m = 3$.
- Thereby four partial matrices are to be considered.
(2) Each partial matrix $\mathbf{G}_l$ consists of.
- one row ⇒ $k = 1$, and
- three columns ⇒ $n = 3$.
(3) All statements are correct:
- Since the current information bit $u_i$ affects all three outputs $x_i^{(1)}, \ x_i^{(2)}$ and $x_i^{(3)}$, $\mathbf{G}_0 = (1, 1, 1)$.
- In contrast, $\mathbf{G}_3 = (1, 1, 0)$ states that only the first two inputs are affected by $u_{i-3}$, but not $x_i^{(3)}$.
(4) Correct is the proposed solution 2:
- The searched generator matrix $\mathbf{G}$ is shown on the right, where the four partial matrices $\mathbf{G}_0, \ ... , \mathbf{G}_3$ are distinguished by color.
- The following vector equation gives the result corresponding to the second proposed solution 2:
- $$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1) \cdot { \boldsymbol{\rm G}}. $$
- The code sequence $\underline{x}$ is thereby equal to the modulo 2 sum of the matrix rows 1, 3 and 4.
- The three code sequences of the individual branches are distinguished by color. For example, the following applies to the lower output:
- $$\underline{x}^{(3)} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.$$
Using the equations given above, this result can be verified:
- $${x}_1^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 + u_{-1} = 1+ (0) = 1 \hspace{0.05cm},$$
- $${x}_2^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_2 + u_{0} = 0+ (0) = 0 \hspace{0.05cm},$$
- $${x}_3^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_3 + u_{1} = 1+1 = 0 \hspace{0.05cm},$$
- $${x}_4^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_4 + u_{2} = 1+0 = 1 \hspace{0.05cm},$$
- $${x}_5^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_5 + u_{3} = 0+ 1 = 1 \hspace{0.05cm}.$$
Notes:
- The memory preallocation with zeros is taken into account here: $u_0 = u_{–1} = 0$.
- If, as assumed here, the information sequence is limited to four bits, then ones can occur in the code sequence up to the position $(4 + m) \cdot n = 21$.