Exercise 3.2Z: Bessel Spectrum
From LNTwww
Consider the complex signal
- $$x(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t) }\hspace{0.05cm}.$$
For example, the equivalent low-pass signal at the output of an angle modulator (PM, FM) can be represented in this form if appropriate normalizations are made.
- When $T_0 = 2π/ω_0$, the Fourier series representation is:
- $$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- These complex Fourier coefficients can be expressed using $n$–th order Bessel functions of the first kind:
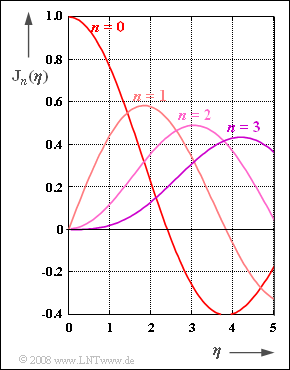
- $${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- These are shown on the graph in the range $0 ≤ η ≤ 5$ . For negative values of $n$ one obtains:
- $${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$
- The series representation of the Bessel functions is:
- $${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$
- If the function values for $n = 0$ and $n = 1$ are known, the Bessel functions for $n ≥ 2$ can be determined from them by iteration:
- $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the page Equivalent low-pass signal in phase modulation.
- The values of the Bessel functions can be found in collections of formulae in table form.
- You can also use the interactive applet Bessel functions of the first kind to solve this task.
Questions
Solution
(1) Only the second answer is correct:
- $x(t)$ is a complex signal that only becomes real in exceptional cases, for example at time $t = 0$.
- A purely imaginary value (at certain times) can only result when $η ≥ π/2$ ⇒ Answer 1 is incorrect.
- For example, when $T_0 = 2π/ω_0$ :
- $$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} + \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi) } ={\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} ) } = x(t)\hspace{0.05cm}.$$
- This signal is periodic. The Fourier series, not the Fourier integral, must be used to calculate the spectral function.
(2) The Fourier coefficients are:
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t) }\cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Combining the two terms and after substituting $α = ω_0 · t$ , we get:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm} = {\rm J}_n (\eta) .$$
- Thus, the second answer is correct.
(3) Using Euler's theorem, the Fourier coefficients can be represented as follows:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha + \frac{\rm j}{2\pi}\cdot \int_{-\pi}^{+\pi} {\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- The integrand of the first integral is an even function of $\alpha$:
- $$I_1 (-\alpha) = {\cos( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\cos( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = I_1 (\alpha) \hspace{0.05cm}.$$
- In contrast, the second integrand is an odd function:
- $$I_2 (-\alpha) = {\sin( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\sin( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= -{\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = -I_2 (\alpha) \hspace{0.05cm}.$$
- Thus, the second integral vanishes and, taking symmetry into account, we obtain:
- $$D_n = \frac{1}{\pi}\cdot \int_{0}^{\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- Thus, the correct solution is Answer 1.
(4) According to the formula for iterative calculation, when $η = 2$:
- $$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$
(5) Due to the given symmetry relation, it further holds that:
- $$ D_{–2} = D_2\hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_{–3} = -D_3 \hspace{0.15cm}\underline {= -0.129} \hspace{0.05cm}.$$