Difference between revisions of "Aufgaben:Exercise 3.2Z: Optimum Cutoff Frequency for Gaussian Low-pass"
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference | ||
}} | }} | ||
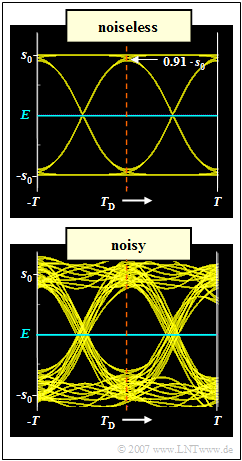
| + | [[File:EN_Dig_Z_3_2_ret.png|right|frame|Noiseless and noisy eye diagrams]] | ||
| − | |||
As in [[Aufgaben:Exercise_3.2:_Eye_Pattern_according_to_Gaussian_Low-Pass|Exercise 3.2]], a binary bipolar redundancy-free binary system with Gaussian receiver filter $H_{\rm G}(f)$ is considered. Its cutoff frequency $f_{\rm G}$ is to be determined such that the worst-case S/N ratio | As in [[Aufgaben:Exercise_3.2:_Eye_Pattern_according_to_Gaussian_Low-Pass|Exercise 3.2]], a binary bipolar redundancy-free binary system with Gaussian receiver filter $H_{\rm G}(f)$ is considered. Its cutoff frequency $f_{\rm G}$ is to be determined such that the worst-case S/N ratio | ||
:$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 72: | Line 72: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The <u>first and third solutions</u> are correct: | + | '''(1)''' The <u>first and third solutions</u> are correct: |
| − | *When calculating the vertical eye opening, the noise component must not be taken into account. This is captured by the noise rms value $\sigma_d$. | + | *When calculating the vertical eye opening, the noise component must not be taken into account. This is captured by the noise rms value $\sigma_d$. |
| − | *If the eye opening were taken from the lower eye diagram, the noise component would be captured twice. | + | *If the eye opening were taken from the lower eye diagram, the noise component would be captured twice. |
| − | *The upper boundary of the inner eye line results for the symbol sequence " $\text{ ...} \, \ -\hspace{-0.1cm}1 \ -\hspace{-0.1cm}1, +1, -\hspace{-0.1cm}1, \ -\hspace{-0.1cm}1, \text{ ...} $ " . | + | *The upper boundary of the inner eye line results for the symbol sequence "$\text{ ...} \, \ -\hspace{-0.1cm}1 \ -\hspace{-0.1cm}1, +1, -\hspace{-0.1cm}1, \ -\hspace{-0.1cm}1, \text{ ...} $" . |
| − | *The long "$-1$" sequence would lead to the value $-s_0$. | + | *The long "$-1$" sequence would lead to the value $-s_0$. |
| − | *In contrast, the "worst–case" sequence leads to the eye line $-s_0 + 2 \cdot g_d(t)$. | + | *In contrast, the "worst–case" sequence leads to the eye line $-s_0 + 2 \cdot g_d(t)$. |
| − | *Thus, at detection time $T_{\rm D} = 0$, with decision threshold $E = 0$: | + | *Thus, at detection time $T_{\rm D} = 0$, with decision threshold $E = 0$: |
:$${\ddot{o}(T_{\rm D})}/{ 2}= 2 \cdot g_0 - s_0 | :$${\ddot{o}(T_{\rm D})}/{ 2}= 2 \cdot g_0 - s_0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
'''(2)''' For the half vertical eye opening holds: | '''(2)''' For the half vertical eye opening holds: | ||
| Line 93: | Line 92: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | A closed eye results according to the given | + | *A closed eye results according to the given applet for |
:$${\rm Q} \left( | :$${\rm Q} \left( | ||
\sqrt{2\pi} \cdot f_{\rm G} \cdot T | \sqrt{2\pi} \cdot f_{\rm G} \cdot T | ||
| Line 101: | Line 100: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | '''(3)''' Using the equations on the information section and the previous calculations, we obtain | |
| − | '''(3)''' Using the equations on the information section and the previous calculations, we obtain | ||
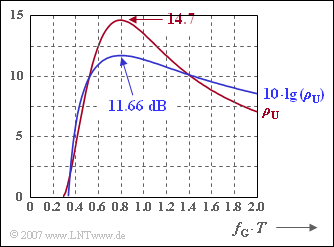
[[File:P_ID1395__Dig_Z_3_2_c.png|right|frame|$\rho_{\rm U}$ as a function of (normalized) cutoff frequency]] | [[File:P_ID1395__Dig_Z_3_2_c.png|right|frame|$\rho_{\rm U}$ as a function of (normalized) cutoff frequency]] | ||
:$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = | :$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = | ||
| Line 110: | Line 108: | ||
\right)\right]^2}{ N_0 \cdot f_{\rm G} / \sqrt{2}}$$ | \right)\right]^2}{ N_0 \cdot f_{\rm G} / \sqrt{2}}$$ | ||
| − | With the specification $E_{\rm B}/N_0 = 10 \ \rm dB $, the following determining equation is obtained: | + | *With the specification $E_{\rm B}/N_0 = 10 \ \rm dB $, the following determining equation is obtained: |
:$$10 \cdot {\rm lg}\hspace{0.1cm} {E_{\rm B}}/{ N_0} = 10 \, {\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$10 \cdot {\rm lg}\hspace{0.1cm} {E_{\rm B}}/{ N_0} = 10 \, {\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{E_{\rm B}}/{ N_0} = {s_0^2 \cdot T}/{ N_0} = 10$$ | {E_{\rm B}}/{ N_0} = {s_0^2 \cdot T}/{ N_0} = 10$$ | ||
| Line 118: | Line 116: | ||
\sqrt{2\pi} \cdot f_{\rm G} \cdot T | \sqrt{2\pi} \cdot f_{\rm G} \cdot T | ||
\right)\right]^2}{ f_{\rm G} \cdot T}\hspace{0.05cm}.$$ | \right)\right]^2}{ f_{\rm G} \cdot T}\hspace{0.05cm}.$$ | ||
| − | The figure shows this function plot as a function of the (normalized) cutoff frequency. For the given cutoff frequencies holds: | + | *The figure shows this function plot as a function of the (normalized) cutoff frequency. For the given cutoff frequencies holds: |
* $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 12.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.04 \ \rm dB},$ | * $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 12.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.04 \ \rm dB},$ | ||
* $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 14.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.66 \ \rm dB},$ | * $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 14.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.66 \ \rm dB},$ | ||
* $f_{\rm G} \cdot T = 1.0\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 13.5 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.30 \ \rm dB}.$ | * $f_{\rm G} \cdot T = 1.0\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 13.5 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.30 \ \rm dB}.$ | ||
| − | From the above graph, one can also see the minimum cutoff frequency ⇒ subtask '''(2)'''. | + | *From the above graph, one can also see the minimum cutoff frequency ⇒ subtask '''(2)'''. |
| − | '''(4)''' The <u>first two solutions</u> are correct: | + | '''(4)''' The <u>first two solutions</u> are correct: |
*The validity of the first statement is evident from the above graph. | *The validity of the first statement is evident from the above graph. | ||
| − | *Since in | + | *Since in $\rho_{\rm U}$ equation the ratio $E_{\rm B}/N_0$ occurs only a factor, the optimization (setting derivative to zero) always leads to the same result independent of $E_{\rm B}/N_0$. |
| − | *The optimal cutoff frequency with respect to $p_{\rm U}$ is approximately optimal with respect to $p_{\rm S}$ as well, but not exactly. | + | *The optimal cutoff frequency with respect to $p_{\rm U}$ is approximately optimal with respect to $p_{\rm S}$ as well, but not exactly. |
| − | *For very large values of $E_{\rm B}/N_0$ (small noise), this approximation is very correct and $p_{\rm S} \ \approx \ p_{\rm U}/4$ holds. | + | *For very large values of $E_{\rm B}/N_0$ (small noise), this approximation is very correct and $p_{\rm S} \ \approx \ p_{\rm U}/4$ holds. |
| − | *In contrast, for large noise | + | *In contrast, for large noise e.g. $10 \cdot {\rm lg} \ E_{\rm B}/N_0 = 0 \ \rm dB$, a smaller optimal cutoff frequency results when the optimization is based on $p_{\rm S}$: |
| − | :: $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} p_{\rm U} = 0.113, p_{\rm S} = 0.102,$ | + | :: $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} p_{\rm U} = 0.113,\hspace{0.4cm} p_{\rm S} = 0.102,$ |
| − | :: $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} p_{\rm U} = 0.129, p_{\rm S} = 0.094.$ | + | :: $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} p_{\rm U} = 0.129,\hspace{0.4cm} p_{\rm S} = 0.094.$ |
| − | *However, the error probabilities are then so large that these results are not practically relevant. | + | *However, the error probabilities are then so large that these results are not practically relevant. |
| − | '''(5)''' With the result of subtask '''(2)''' ⇒ $E_{\rm B}/N_0 = 10$ and $f_{\rm G} \cdot T = 0.8$ holds: | + | '''(5)''' With the result of subtask '''(2)''' ⇒ $E_{\rm B}/N_0 = 10$ and $f_{\rm G} \cdot T = 0.8$ holds: |
:$${\ddot{o}(T_{\rm D})}/{ s_0} = 2 \cdot \left [ 1- 4 \cdot {\rm Q} \left( | :$${\ddot{o}(T_{\rm D})}/{ s_0} = 2 \cdot \left [ 1- 4 \cdot {\rm Q} \left( | ||
\sqrt{2\pi} \cdot 0.8 \right)\right] = 2 \cdot \left [ 1- 4 | \sqrt{2\pi} \cdot 0.8 \right)\right] = 2 \cdot \left [ 1- 4 | ||
Latest revision as of 14:25, 10 October 2022
As in Exercise 3.2, a binary bipolar redundancy-free binary system with Gaussian receiver filter $H_{\rm G}(f)$ is considered. Its cutoff frequency $f_{\rm G}$ is to be determined such that the worst-case S/N ratio
- $$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right)$$
becomes maximum and thus the worst-case error probability $p_{\rm U}$ becomes minimum. The thus optimized cutoff frequency $f_{\rm G, \ opt}$ usually also leads to the minimum mean symbol error probability $p_{\rm S, \ min}$.
In the above equation, the following system quantities are used:
- $\sigma_d^2$ is the detection noise power. For a Gaussian receiver filter holds:
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.$$
- $\ddot{o}(T_{\rm D})$ indicates the "eye opening". The detection time is always assumed to be $T_{\rm D} = 0$.
- For a Gaussian receiver filter, the vertical eye opening $\ddot{o}(T_{\rm D})$ can be expressed solely by the amplitude $s_0$ of the basic transmission pulse $($upper boundary line in the noiseless eye diagram$)$ and the maximum value $g_0$ of the basic detection pulse. $g_0$ is to be calculated as follows:
- $$g_0 = g_d(t = 0) = s_0 \cdot \big [1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\big]\hspace{0.05cm}.$$
The graph shows the eye diagrams of the sought configuration with optimal cutoff frequency.
- In the upper diagram, noise is not considered.
- The lower diagram, on the other hand, is valid with AWGN noise for $10 \cdot {\rm lg} \ E_{\rm B}/N_0 = 10 \ \rm dB$.
Notes:
- The exercise belongs to the chapter "Error Probability with Intersymbol Interference".
- Use our HTML5/JavaScript applet "Complementary Gaussian Error Functions" for the numerical evaluation of the Q–function.
Questions
Solution
- When calculating the vertical eye opening, the noise component must not be taken into account. This is captured by the noise rms value $\sigma_d$.
- If the eye opening were taken from the lower eye diagram, the noise component would be captured twice.
- The upper boundary of the inner eye line results for the symbol sequence "$\text{ ...} \, \ -\hspace{-0.1cm}1 \ -\hspace{-0.1cm}1, +1, -\hspace{-0.1cm}1, \ -\hspace{-0.1cm}1, \text{ ...} $" .
- The long "$-1$" sequence would lead to the value $-s_0$.
- In contrast, the "worst–case" sequence leads to the eye line $-s_0 + 2 \cdot g_d(t)$.
- Thus, at detection time $T_{\rm D} = 0$, with decision threshold $E = 0$:
- $${\ddot{o}(T_{\rm D})}/{ 2}= 2 \cdot g_0 - s_0 \hspace{0.05cm}.$$
(2) For the half vertical eye opening holds:
- $${\ddot{o}(T_{\rm D})}/{ 2} \ = \ 2 \cdot g_0 - s_0 = 2 \cdot s_0 \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] - s_0 = s_0 \cdot\left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] \hspace{0.05cm}.$$
- A closed eye results according to the given applet for
- $${\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right) \ge 0.25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sqrt{2\pi} \cdot f_{\rm G} \cdot T< 0.675\hspace{0.3cm}\Rightarrow \hspace{0.3cm} f_{\rm G, min} \cdot T \approx \frac{0.675}{2.5}\hspace{0.15cm}\underline { \approx 0.27} \hspace{0.05cm}.$$
(3) Using the equations on the information section and the previous calculations, we obtain
- $$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = \frac{s_0^2 \cdot\left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]^2}{ N_0 \cdot f_{\rm G} / \sqrt{2}}$$
- With the specification $E_{\rm B}/N_0 = 10 \ \rm dB $, the following determining equation is obtained:
- $$10 \cdot {\rm lg}\hspace{0.1cm} {E_{\rm B}}/{ N_0} = 10 \, {\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {E_{\rm B}}/{ N_0} = {s_0^2 \cdot T}/{ N_0} = 10$$
- $$\Rightarrow \hspace{0.3cm} \rho_{\rm U} = 10 \cdot \sqrt{2} \cdot \frac{ \left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]^2}{ f_{\rm G} \cdot T}\hspace{0.05cm}.$$
- The figure shows this function plot as a function of the (normalized) cutoff frequency. For the given cutoff frequencies holds:
- $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 12.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.04 \ \rm dB},$
- $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 14.7 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.66 \ \rm dB},$
- $f_{\rm G} \cdot T = 1.0\text{:} \hspace{0.4cm} \rho_{\rm U} \approx 13.5 \Rightarrow 10 \cdot \rm lg \ \rho_{\rm U} \ \underline {\approx \ 11.30 \ \rm dB}.$
- From the above graph, one can also see the minimum cutoff frequency ⇒ subtask (2).
(4) The first two solutions are correct:
- The validity of the first statement is evident from the above graph.
- Since in $\rho_{\rm U}$ equation the ratio $E_{\rm B}/N_0$ occurs only a factor, the optimization (setting derivative to zero) always leads to the same result independent of $E_{\rm B}/N_0$.
- The optimal cutoff frequency with respect to $p_{\rm U}$ is approximately optimal with respect to $p_{\rm S}$ as well, but not exactly.
- For very large values of $E_{\rm B}/N_0$ (small noise), this approximation is very correct and $p_{\rm S} \ \approx \ p_{\rm U}/4$ holds.
- In contrast, for large noise e.g. $10 \cdot {\rm lg} \ E_{\rm B}/N_0 = 0 \ \rm dB$, a smaller optimal cutoff frequency results when the optimization is based on $p_{\rm S}$:
- $f_{\rm G} \cdot T = 0.8\text{:} \hspace{0.4cm} p_{\rm U} = 0.113,\hspace{0.4cm} p_{\rm S} = 0.102,$
- $f_{\rm G} \cdot T = 0.6\text{:} \hspace{0.4cm} p_{\rm U} = 0.129,\hspace{0.4cm} p_{\rm S} = 0.094.$
- However, the error probabilities are then so large that these results are not practically relevant.
(5) With the result of subtask (2) ⇒ $E_{\rm B}/N_0 = 10$ and $f_{\rm G} \cdot T = 0.8$ holds:
- $${\ddot{o}(T_{\rm D})}/{ s_0} = 2 \cdot \left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot 0.8 \right)\right] = 2 \cdot \left [ 1- 4 \cdot 0.022\right]\hspace{0.15cm}\underline { = 1.824} \hspace{0.05cm},$$
- $${\sigma_d^2}/{ s_0^2} = \frac{N_0 \cdot f_{\rm G} }{\sqrt{2}\cdot s_0^2}= \frac{N_0 }{s_0^2 \cdot T} \cdot \frac{f_{\rm G} \cdot T}{\sqrt{2}} = 0.1 \cdot \frac{0.8}{\sqrt{2}} \approx 0.0566 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\sigma_d}/{ s_0}\hspace{0.15cm}\underline { \approx 0.238} \hspace{0.05cm},$$
- $$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})]^2}{ 4 \cdot \sigma_d^2} = \frac{1.824^2}{ 4 \cdot 0.0566}\approx 14.7 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}\hspace{0.15cm}\underline {\approx 11.66\, {\rm dB}} \hspace{0.05cm}.$$
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) = {\rm Q} \left( \sqrt{14.7} \right) \hspace{0.15cm}\underline { \approx 6.4 \cdot 10^{-5}}\hspace{0.05cm}.$$