Difference between revisions of "Aufgaben:Exercise 3.3: From the Signal to the Spectrum"
From LNTwww
| (37 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Special_Cases_of_Impulse_Signals |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sig_A_3_3.png|250px|right|frame|Rectangular pulse and its spectrum]] |
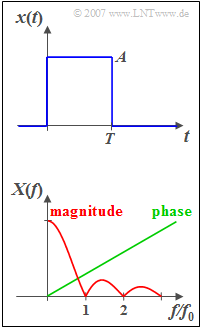
| − | + | A rectangular pulse $x(t)$ with duration $T = 50\,\text{µs}$ and height $A = 2\,\text{V}$ is considered. At the jumping points at $t = 0$ and $t = T$ the signal value is $A/2$ in each case, but this has no influence on the solution of the task. | |
| − | |||
| − | $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$ | + | In the lower graph, the corresponding spectral function is sketched qualitatively according to magnitude and phase. It is valid: |
| + | |||
| + | :$$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$ | ||
| − | + | The analytical function progression of $X(f)$ is to be determined. | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This task belongs to the chapter [[Signal_Representation/Special_Cases_of_Pulses|Special Cases of Pulses]]. | ||
| + | *Use one of the functions $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$. | ||
| + | *The following trigonometric transformations are given: | ||
| + | |||
| + | :$$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$ | ||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the spectral function $X(f)$ in general. What value results at the frequency $f=10\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $Re[X(f=10 \text{kHz})] =$ { | + | ${\rm Re}\big[X(f=10 \,\text{kHz})\big] \ = \ $ { 0. } $\text{mV/Hz}$ |
| − | $Im[X(f=10 \text{kHz})] =$ { - 0. | + | ${\rm Im}\big[X(f=10\, \text{kHz})\big]\ = \ $ { -0.064--0.06 } $\text{mV/Hz}$ |
| − | { | + | {Calculate the magnitude function $|X(f)|$ in general. What values result for the frequencies $f = 0$ and $f=20 \,\text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $|X(f=0)| =$ { 0.1 3% } mV/Hz | + | $|X(f=0)|\ = \ $ { 0.1 3% } $\text{mV/Hz}$ |
| − | $|X(f= 20 \text{kHz})| =$ { | + | $|X(f=20\, \text{kHz})|\ = \ $ { 0. } $\text{mV/Hz}$ |
| − | { | + | {Which of the following statements are true regarding $|X(f)|$? |
|type="[]"} | |type="[]"} | ||
| − | + $|X(f)|$ | + | + $|X(f)|$ has zeros at multiples of $f_0 = 1/T$. |
| − | - $|X(f)|$ | + | - $|X(f)|$ has zeros at multiples of $f_0 = 1/(2T)$. |
| − | + In | + | + In the middle between two zeros $|X(f)| = |A/(\pi f)|$ is true. |
| − | { | + | {Calculate the phase function $\varphi (f)$. What phase angle (in degrees) results at the frequency $f=10\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi (f=10\, \text{kHz})\ = \ $ { 90 1% } $\text{deg}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' With the abbreviation $\omega = 2\pi f$ the spectral function is according to the first Fourier integral: |
| − | $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$ | + | :$$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$ |
| − | + | *After integration and insertion of the limits, it follows: | |
| − | $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$ | + | :$${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$ |
| − | $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega }\left( {1 - \cos ( {\omega T} )} \right).$$ | + | :$${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$ |
| − | + | *For the frequency $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ we get: | |
| − | $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$ | + | :$${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$ |
| + | |||
| + | :$${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | |||
| − | '''2 | + | '''(2)''' The magnitude square is the sum of the real and imaginary parts, squared in each case: |
| − | $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\ | + | :$$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$ |
| − | + | *Because of $\sin^2(\alpha) + \cos^2(\alpha) = 1$ , this can also be written: | |
| − | $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }}\ | + | :$$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$ |
| − | + | *Setting $\omega = 2\pi f$ and taking the root, we obtain, under the condition $A > 0$: | |
| − | $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$ | + | :$$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$ |
| − | + | *With the shortcuts $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$ the results are: | |
| − | $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$ | + | :$$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|,$$ |
| + | :$$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm sinc} ( fT ) \right|.$$ | ||
| − | + | *The spectral value at the frequency $f = 1/T = \text{20 kHz}$ is given by | |
| − | $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$ | + | :$$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$ |
| − | + | *When calculating the value for $f = 0$ the quotient is $\text{"0 divided by 0"}$. By applying [https://en.wikipedia.org/wiki/L%27H%C3%B4pital%27s_rule L'Hospitals rule] the limiting value can be calculated: | |
| − | $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$ | + | :$$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$ |
| − | + | *From this follows: | |
| − | $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= | + | :$$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$ |
| + | |||
| + | *This result is obvious because, according to the first Fourier integral, the spectral value at $f = 0$ corresponds exactly to the area under the time function. | ||
| − | |||
| − | |||
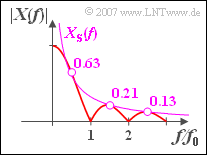
| − | '''3 | + | [[File:P_ID563__Sig_A_3_3_c.png|right|frame|Magnitude spectrum of the rectangular pulse]] |
| − | + | '''(3)''' The <u>proposed solutions 1 and 3</u> are correct: | |
| + | *According to the result of subtask '''(2)''' the zeros occur at the distance $f_0 = 1/T$ . | ||
| + | *With $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ the real part is $0$, but not the imaginary part. | ||
| + | *With the arguments $f \cdot T = 0.5,\ 1.5,\ 2.5,\hspace{0.05cm}\text{ ... }$ the sine function is in each case equal in magnitude to $1$, and it holds: | ||
| − | $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$ | + | :$$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$ |
| + | |||
| + | *At other frequencies, $X_{\rm S}(f)$ serves as an upper bound, i.e. $|Xf)| \leq X_{\rm S}(f)$ always applies. | ||
| + | *In the sketch, this bound is drawn as a violet curve in addition to $|X(f)|$. | ||
| + | |||
| − | |||
| − | |||
| − | '''4 | + | '''(4)''' According to the definition on the information page, one can calculate the phase function as follows: |
| − | $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$ | + | :$$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$ |
| − | + | *With the results from subtask '''(1)''' the following thus applies: | |
| − | $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$ | + | :$$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$ |
| − | + | *The argument of this function is equal to $\tan(\omega T/2) = \tan(\pi fT)$ according to the specification. From this follows a linearly increasing course with frequency: | |
| − | $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$ | + | :$$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$ |
| − | + | *With $f = 10\,\text{kHz}$ and $T = 50\,\text{µs}$ one obtains from this the phase angle $\pi /2$ corresponding to $\underline{90^{\circ}}$ . | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.2 Special Cases of Pulses^]] |
Latest revision as of 11:36, 23 April 2021
A rectangular pulse $x(t)$ with duration $T = 50\,\text{µs}$ and height $A = 2\,\text{V}$ is considered. At the jumping points at $t = 0$ and $t = T$ the signal value is $A/2$ in each case, but this has no influence on the solution of the task.
In the lower graph, the corresponding spectral function is sketched qualitatively according to magnitude and phase. It is valid:
- $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$
The analytical function progression of $X(f)$ is to be determined.
Hints:
- This task belongs to the chapter Special Cases of Pulses.
- Use one of the functions $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$.
- The following trigonometric transformations are given:
- $$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$
Questions
Solution
(1) With the abbreviation $\omega = 2\pi f$ the spectral function is according to the first Fourier integral:
- $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$
- After integration and insertion of the limits, it follows:
- $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$
- $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$
- For the frequency $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ we get:
- $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$
- $${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) The magnitude square is the sum of the real and imaginary parts, squared in each case:
- $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$
- Because of $\sin^2(\alpha) + \cos^2(\alpha) = 1$ , this can also be written:
- $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$
- Setting $\omega = 2\pi f$ and taking the root, we obtain, under the condition $A > 0$:
- $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$
- With the shortcuts $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$ the results are:
- $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|,$$
- $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm sinc} ( fT ) \right|.$$
- The spectral value at the frequency $f = 1/T = \text{20 kHz}$ is given by
- $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$
- When calculating the value for $f = 0$ the quotient is $\text{"0 divided by 0"}$. By applying L'Hospitals rule the limiting value can be calculated:
- $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$
- From this follows:
- $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$
- This result is obvious because, according to the first Fourier integral, the spectral value at $f = 0$ corresponds exactly to the area under the time function.
(3) The proposed solutions 1 and 3 are correct:
- According to the result of subtask (2) the zeros occur at the distance $f_0 = 1/T$ .
- With $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ the real part is $0$, but not the imaginary part.
- With the arguments $f \cdot T = 0.5,\ 1.5,\ 2.5,\hspace{0.05cm}\text{ ... }$ the sine function is in each case equal in magnitude to $1$, and it holds:
- $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$
- At other frequencies, $X_{\rm S}(f)$ serves as an upper bound, i.e. $|Xf)| \leq X_{\rm S}(f)$ always applies.
- In the sketch, this bound is drawn as a violet curve in addition to $|X(f)|$.
(4) According to the definition on the information page, one can calculate the phase function as follows:
- $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$
- With the results from subtask (1) the following thus applies:
- $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$
- The argument of this function is equal to $\tan(\omega T/2) = \tan(\pi fT)$ according to the specification. From this follows a linearly increasing course with frequency:
- $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$
- With $f = 10\,\text{kHz}$ and $T = 50\,\text{µs}$ one obtains from this the phase angle $\pi /2$ corresponding to $\underline{90^{\circ}}$ .