Difference between revisions of "Aufgaben:Exercise 3.4: Trapezoidal Spectrum and Pulse"
| (41 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Transform_Laws |
}} | }} | ||
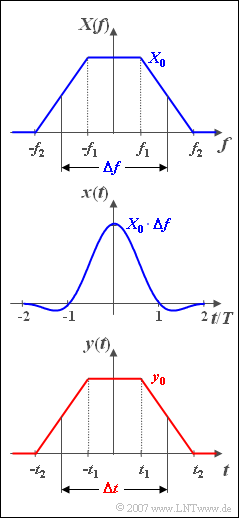
| − | [[File:P_ID508__Sig_A_3_4.png|250px|right| | + | [[File:P_ID508__Sig_A_3_4.png|250px|right|frame|Trapezoidal spectrum & trapezoidal pulse]] |
| − | + | We consider here a trapezoidal spectral function $X(f)$ according to the upper graph, which is completely described by the three parameters $X_0$, $f_1$ and $f_2$. For the two corner frequencies, $f_2 > 0$ and $0 \leq f_1 \leq f_2$ always apply. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Instead of the corner frequencies $f_1$ and $f_2$ , the following two descriptive variables can also be used: | ||
| + | *the [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|equivalent bandwidth]]: | ||
| + | :$$\Delta f = f_1 + f_2,$$ | ||
| + | *the so-called [[Linear_and_Time_Invariant_Systems/Einige_systemtheoretische_Tiefpassfunktionen#Trapez.E2.80.93Tiefpass|rolloff factor]] (in the frequency domain): | ||
| + | :$$r_{\hspace{-0.05cm}f} = \frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}.$$ | ||
| − | + | With these quantities, the associated time function (see middle graph) is: | |
| − | $$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot | + | :$$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f\cdot t} ).$$ |
| − | + | Here $\text{si}(x) = \text{sin}(x)/x$ is the so-called "splitting function". | |
| − | |||
| − | + | In this example, the numerical values $X_0 = 10^{–3}\,\text{V/Hz}$, $f_1 = 1\,\text{kHz}$ and $f_2 = 3\,\text{kHz}$ are to be used. The time $T = 1/\Delta f$ is only used for normative purpose. | |
| − | + | ||
| − | + | In the subtask '''(3)''' a trapezoidal signal $y(t)$ is considered, which is identical in shape to the spectrum $X(f)$. | |
| + | |||
| + | The following can be used here as descriptive variables: | ||
| + | *the pulse amplitude $y_0 = y(t = 0)$, | ||
| + | *the [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|equivalent pulse duration]] (defined via the rectangle–in–time with the same area): | ||
| + | |||
| + | :$$\Delta t = t_1 + t_2,$$ | ||
| + | |||
| + | *the rolloff factor (in the time domain) with comparable definition as $r_f$: | ||
| − | $$\ | + | :$$r_{\hspace{-0.05cm}t} = \frac{ {t_2 - t_1 }}{ {t_2 + t_1 }}.$$ |
| + | |||
| + | Let be $y_0 = 4\,\text{V}$, $\Delta t = 1\,\text{ms}$ and $r_t = 0.5$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | ''Hints:'' | |
| + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_Theorems|Fourier Transform Theorems]]. | ||
| + | *Use the [[Signal_Representation/Fourier_Transform_Theorems#Duality_Theorem|Duality Theorem]] and the [[Signal_Representation/Fourier_Transform_Theorems#Similarity_Theorem|Similarity Theorem]]. | ||
| − | + | *You can check your results using the two interactive applets | |
| + | :[[Applets:Pulses_and_Spectra|Pulses and Spectra]], | ||
| + | :[[Applets:Frequency_%26_Impulse_Responses|Frequency & Impulse Responses]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the equivalent bandwidth and the rolloff factor of the spectrum $X(f)$ for the given parameters? |
|type="{}"} | |type="{}"} | ||
| − | $\Delta f =$ { 4 } kHz | + | $\Delta f \ = \ $ { 4 3% } $\text{kHz}$ |
| − | $ | + | $r_{\hspace{-0.05cm}f} \hspace{0.35cm} = \ $ { 0.5 3% } |
| − | { | + | {What are the signal values of $x(t)$ at $t = 0$, $t = T$ and $t = T/2$? |
|type="{}"} | |type="{}"} | ||
| − | $x(t=0) =$ { 4 } V | + | $x(t=0)\hspace{0.2cm} = \ $ { 4 3% } $\text{V}$ |
| − | $x(t=T | + | $x(t=T)\ = \ $ { 0. } $\text{V}$ |
| − | $x(t=T) =$ { | + | $x(t=T/2)\ = \ $ { 2.293 3% } $\text{V}$ |
| − | { | + | {What is the spectrum $Y(f)$ of the trapezoidal pulse with $y_0 = 4\,\text{V}$, $\Delta t = 1\,\text{ms}$ and $r_t = 0.5$? <br>What are the spectral values at the given frequencies? |
|type="{}"} | |type="{}"} | ||
| − | $Y(f = 0) | + | $Y(f = 0)\hspace{0.2cm} = \ $ { 4 3% } $\text{mV/Hz}$ |
| − | $Y(f = 0.5 \text{kHz}) =$ { 2.293 3% } mV/Hz | + | $Y(f = 0.5 \,\text{kHz})\ = \ $ { 2.293 3% } $\text{mV/Hz}$ |
| − | $Y(f = 1 \text{kHz}) =$ { 0 } mV/Hz | + | $Y(f = 1.0 \,\text{kHz})\ = \ $ { 0. } $\text{mV/Hz}$ |
| − | { | + | {Which spectral values result with $y_0 = 8\,\text{V}$, $\Delta t = 0.5\,\text{ms }$ and $r_t = 0.5$? |
|type="{}"} | |type="{}"} | ||
| − | $Y(f=0) =$ { 4 } mV/Hz | + | $Y(f=0)\hspace{0.2cm}= \ $ { 4 3% } $\text{mV/Hz}$ |
| − | $Y(f=1\text{kHz}) =$ { 2.293 3% } mV/Hz | + | $Y(f=1.0 \,\text{kHz})\ = \ $ { 2.293 3% } $\text{mV/Hz}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The equivalent bandwidth is (by definition) equal to the width of the equal-area rectangle: |
| − | + | :$$\Delta f = f_1 + f_2 \hspace{0.15 cm}\underline{= 4\;{\rm{kHz}}}{\rm{.}}$$ | |
| + | *For the rolloff factor holds: | ||
| − | '''2 | + | :$${ {r_{\hspace{-0.05cm}f} = }}\frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}\hspace{0.15 cm}\underline{ = 0.5}.$$ |
| − | + | ||
| + | |||
| + | '''(2)''' The maximum value of the pulse $x(t)$ occurs at time $t = 0$ : | ||
| + | |||
| + | :$$x_0 = x(t = 0) = X_0 \cdot \Delta f \hspace{0.15 cm}\underline{= 4\, \text{V}}.$$ | ||
| + | |||
| + | *At time $t = T = 1/\Delta f$ applies due to $\text{si}(\pi) = 0$: | ||
| − | + | :$$x( {t = T} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}.$$ | |
| + | |||
| + | *Also at all multiples of $T$: $x(t)$ exhibits zero crossings. At time $t = T/2$ holds: | ||
| − | '''3 | + | :$$x( {t = T/2} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits}( { { {\rm{\pi }}}/{4}} ) = x_0 \cdot \frac{ { 1 \cdot \sqrt 2 /2}}{ { {\rm{\pi /}}2 \cdot {\rm{\pi /4}}}} = x_0 \cdot \frac{ {4 \cdot \sqrt 2 }}{ { {\rm{\pi }}^{\rm{2}} }} \hspace{0.15 cm}\underline{= 2.293\;{\rm{V}}}{\rm{.}}$$ |
| + | |||
| + | |||
| + | '''(3)''' The time function associated with the trapezoidal spectrum $X(f)$ is according to the specification: | ||
| − | + | :$$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_f \cdot \Delta f \cdot t} ).$$ | |
| + | |||
| + | *Since both $X(f)$ and $x(t)$ are real and, moreover, $y(t)$ is of the same form as $X(f),$ we obtain, taking into account all equivalences for the spectral function of the trapezoidal pulse: | ||
| − | + | :$$Y( f ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta t \cdot f} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_t \cdot \Delta t \cdot f} ).$$ | |
| + | |||
| + | *In particular, holds: | ||
| + | :$$Y( {f = 0} ) = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \;{\rm{mV/Hz}}}{\rm{,}}$$ | ||
| + | |||
| + | :$$Y( {f = 0.5\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293 \;{\rm{mV/Hz}}}{\rm{,}}$$ | ||
| + | |||
| + | :$$Y( {f = 1\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}\;{\rm{.}}$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The spectral value at frequency $f = 0$ is not changed: | ||
| + | :$$Y_0 = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \,\rm{mV/Hz}}.$$ | ||
| + | |||
| + | *But since the time function is now only half as wide, the spectrum widens by a factor of $2$: | ||
| + | |||
| + | :$$Y( {f = 1\;{\rm{kHz}}} ) = Y_0 \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293\,{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | + | *In subtask '''(3)''' this spectral value occurred at the frequency $f = 0.5\,\rm{kHz}$ . | |
| − | ''' | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.3 Fourier Transform Theorems^]] |
Latest revision as of 15:17, 24 May 2021
We consider here a trapezoidal spectral function $X(f)$ according to the upper graph, which is completely described by the three parameters $X_0$, $f_1$ and $f_2$. For the two corner frequencies, $f_2 > 0$ and $0 \leq f_1 \leq f_2$ always apply.
Instead of the corner frequencies $f_1$ and $f_2$ , the following two descriptive variables can also be used:
- the equivalent bandwidth:
- $$\Delta f = f_1 + f_2,$$
- the so-called rolloff factor (in the frequency domain):
- $$r_{\hspace{-0.05cm}f} = \frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}.$$
With these quantities, the associated time function (see middle graph) is:
- $$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f\cdot t} ).$$
Here $\text{si}(x) = \text{sin}(x)/x$ is the so-called "splitting function".
In this example, the numerical values $X_0 = 10^{–3}\,\text{V/Hz}$, $f_1 = 1\,\text{kHz}$ and $f_2 = 3\,\text{kHz}$ are to be used. The time $T = 1/\Delta f$ is only used for normative purpose.
In the subtask (3) a trapezoidal signal $y(t)$ is considered, which is identical in shape to the spectrum $X(f)$.
The following can be used here as descriptive variables:
- the pulse amplitude $y_0 = y(t = 0)$,
- the equivalent pulse duration (defined via the rectangle–in–time with the same area):
- $$\Delta t = t_1 + t_2,$$
- the rolloff factor (in the time domain) with comparable definition as $r_f$:
- $$r_{\hspace{-0.05cm}t} = \frac{ {t_2 - t_1 }}{ {t_2 + t_1 }}.$$
Let be $y_0 = 4\,\text{V}$, $\Delta t = 1\,\text{ms}$ and $r_t = 0.5$.
Hints:
- This exercise belongs to the chapter Fourier Transform Theorems.
- Use the Duality Theorem and the Similarity Theorem.
- You can check your results using the two interactive applets
Questions
Solution
- $$\Delta f = f_1 + f_2 \hspace{0.15 cm}\underline{= 4\;{\rm{kHz}}}{\rm{.}}$$
- For the rolloff factor holds:
- $${ {r_{\hspace{-0.05cm}f} = }}\frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}\hspace{0.15 cm}\underline{ = 0.5}.$$
(2) The maximum value of the pulse $x(t)$ occurs at time $t = 0$ :
- $$x_0 = x(t = 0) = X_0 \cdot \Delta f \hspace{0.15 cm}\underline{= 4\, \text{V}}.$$
- At time $t = T = 1/\Delta f$ applies due to $\text{si}(\pi) = 0$:
- $$x( {t = T} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}.$$
- Also at all multiples of $T$: $x(t)$ exhibits zero crossings. At time $t = T/2$ holds:
- $$x( {t = T/2} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits}( { { {\rm{\pi }}}/{4}} ) = x_0 \cdot \frac{ { 1 \cdot \sqrt 2 /2}}{ { {\rm{\pi /}}2 \cdot {\rm{\pi /4}}}} = x_0 \cdot \frac{ {4 \cdot \sqrt 2 }}{ { {\rm{\pi }}^{\rm{2}} }} \hspace{0.15 cm}\underline{= 2.293\;{\rm{V}}}{\rm{.}}$$
(3) The time function associated with the trapezoidal spectrum $X(f)$ is according to the specification:
- $$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_f \cdot \Delta f \cdot t} ).$$
- Since both $X(f)$ and $x(t)$ are real and, moreover, $y(t)$ is of the same form as $X(f),$ we obtain, taking into account all equivalences for the spectral function of the trapezoidal pulse:
- $$Y( f ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta t \cdot f} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_t \cdot \Delta t \cdot f} ).$$
- In particular, holds:
- $$Y( {f = 0} ) = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \;{\rm{mV/Hz}}}{\rm{,}}$$
- $$Y( {f = 0.5\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293 \;{\rm{mV/Hz}}}{\rm{,}}$$
- $$Y( {f = 1\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}\;{\rm{.}}$$
(4) The spectral value at frequency $f = 0$ is not changed:
- $$Y_0 = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \,\rm{mV/Hz}}.$$
- But since the time function is now only half as wide, the spectrum widens by a factor of $2$:
- $$Y( {f = 1\;{\rm{kHz}}} ) = Y_0 \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293\,{\rm{mV/Hz}}}{\rm{.}}$$
- In subtask (3) this spectral value occurred at the frequency $f = 0.5\,\rm{kHz}$ .