Exercise 3.4: Trapezoidal Spectrum and Pulse

• Return to book

Trapezspektrum & Trapezimpuls

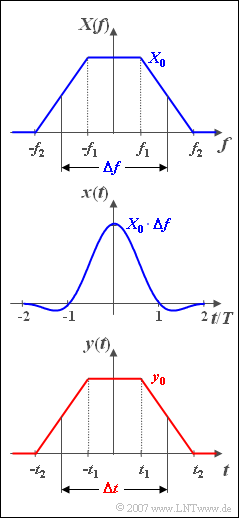
We consider here a trapezoidal spectral function  $X(f)$  according to the upper graph, which is completely described by the three parameters  $X_0$,  $f_1$  and  $f_2$ . For the two corner frequencies,  $f_2 > 0$  and  $0 \leq f_1 \leq f_2$ always apply.

Instead of the corner frequencies  $f_1$  and  $f_2$ , the following two descriptive variables can also be used:

• the  equivalent bandwidth:

$$\Delta f = f_1 + f_2,$$

• the so-called  rolloff factor  (in the frequency domain):

$$r_f = \frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}.$$

With these quantities, the associated time function (see middle graph) is:-

$$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm \pi} \cdot r_f \cdot \Delta f\cdot t} ).$$

Here  $\text{si}(x) = \text{sin}(x)/x$  is the so-called splitting function.

In this example, the numerical values  $X_0 = 10^{–3}\,\text{V/Hz}$,  $f_1 = 1\,\text{kHz}$  and  $f_2 = 3\,\text{kHz}$  are to be used. The time  $T = 1/\Delta f$  is only used for standardisation purposes. From subtask  (3)  a trapezoidal signal  $y(t)$  is considered, which is identical in shape to the spectrum  $X(f)$ .

The following can be used here as descriptive variables:

• the pulse amplitude  $y_0 = y(t = 0)$,
• the  equivalent pulse duration  (defined via the rectangle with the same area):

$$\Delta t = t_1 + t_2,$$

• the rolloff factor (in the time domain) with comparable definition as  $r_f$:

$$r_t = \frac{ {t_2 - t_1 }}{ {t_2 + t_1 }}.$$

Let  $y_0 = 4\,\text{V}$,  $\Delta t = 1\,\text{ms}$  and  $r_t = 0.5$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Gesetzmäßigkeiten der Fouriertransformation.
• Verwenden Sie zur Lösung den  Vertauschungssatz  und den  Ähnlichkeitssatz.

• Sie können Ihre Ergebnisse anhand der beiden interaktiven Applets  Impulse und Spektren  sowie  Frequenzgang und Impulsantwort  überprüfen.

Fragebogen

1

Wie groß sind bei den gegebenen Parametern die äquivalente Bandbreite und der Rolloff-Faktor des Spektrums  $X(f)$?

$\Delta f \ = \ $  $\text{kHz}$

$r_f \hspace{0.35cm} = \ $

2

Wie groß sind die Signalwerte von  $x(t)$  bei  $t = 0$,  $t = T$  und  $t = T/2$?

$x(t=0)\hspace{0.2cm} = \ $  $\text{V}$

$x(t=T)\ = \ $  $\text{V}$

$x(t=T/2)\ = \ $  $\text{V}$

3

Wie lautet das Spektrum  $Y(f)$  des Trapezimpulses mit  $y_0 = 4\,\text{V}$,  $\Delta t = 1\,\text{ms}$  und  $r_t = 0.5$?
Wie groß sind die Spektralwerte bei den angegebenen Frequenzen?

$Y(f = 0)\hspace{0.2cm} = \ $  $\text{mV/Hz}$

$Y(f = 0.5 \,\text{kHz})\ = \ $  $\text{mV/Hz}$

$Y(f = 1.0 \,\text{kHz})\ = \ $  $\text{mV/Hz}$

4

Welche Spektralwerte ergeben sich mit  $y_0 = 8\,\text{V}$,  $\Delta t = 0.5\,\text{ms }$  und  $r_t = 0.5$?

$Y(f=0)\hspace{0.2cm}= \ $  $\text{mV/Hz}$

$Y(f=1.0 \,\text{kHz})\ = \ $  $\text{mV/Hz}$

Musterlösung

Solution

(1)  Die äquivalente Bandbreite ist per Definition gleich der Breite des flächengleichen Rechtecks:

$$\Delta f = f_1 + f_2 \hspace{0.15 cm}\underline{= 4\;{\rm{kHz}}}{\rm{.}}$$

• Für den Rolloff-Faktor gilt:

$${ {r_f = }}\frac{ {f_2 - f_1 }}{ {f_2 + f_1 }}\hspace{0.15 cm}\underline{ = 0.5}.$$

(2)  Der Maximalwert des Impulses  $x(t)$  tritt zum Zeitpunkt  $t = 0$  auf:

$$x_0 = x(t = 0) = X_0 \cdot \Delta f \hspace{0.15 cm}\underline{= 4\, \text{V}}.$$

• Zum Zeitpunkt  $t = T = 1/\Delta f$  gilt aufgrund von  $\text{si}(\pi) = 0$:

$$x( {t = T} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}.$$

• Auch bei allen Vielfachen von  $T$  weist  $x(t)$  Nulldurchgänge auf. Zum Zeitpunkt  $t = T/2$  gilt:

$$x( {t = T/2} ) = x_0 \cdot {\mathop{\rm si}\nolimits} ( { { {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits}( { { {\rm{\pi }}}/{4}} ) = x_0 \cdot \frac{ { 1 \cdot \sqrt 2 /2}}{ { {\rm{\pi /}}2 \cdot {\rm{\pi /4}}}} = x_0 \cdot \frac{ {4 \cdot \sqrt 2 }}{ { {\rm{\pi }}^{\rm{2}} }} \hspace{0.15 cm}\underline{= 2.293\;{\rm{V}}}{\rm{.}}$$

(3)  Die zum trapezförmigen Spektrum  $X(f)$  zugehörige Zeitfunktion lautet entsprechend der Angabe:

$$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_f \cdot \Delta f \cdot t} ).$$

• Da sowohl  $X(f)$  als auch  $x(t)$  reell sind und zudem  $y(t)$  formgleich mit  $X(f)$  ist, erhält man unter Berücksichtigung aller Äquivalenzen für die Spektralfunktion des Trapezimpulses:

$$Y( f ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot \Delta t \cdot f} ) \cdot {\mathop{\rm si}\nolimits} ( { {\rm{\pi }} \cdot r_t \cdot \Delta t \cdot f} ).$$

• Insbesondere gilt:

$$Y( {f = 0} ) = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \;{\rm{mV/Hz}}}{\rm{,}}$$

$$Y( {f = 0.5\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293 \;{\rm{mV/Hz}}}{\rm{,}}$$

$$Y( {f = 1\;{\rm{kHz}}} ) = y_0 \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {\rm{\pi }} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} )\hspace{0.15 cm}\underline{ = 0}\;{\rm{.}}$$

(4)  Der Spektralwert bei der Frequenz  $f = 0$  wird nicht verändert:  

$$Y_0 = y_0 \cdot \Delta t \hspace{0.15 cm}\underline{= 4 \,\rm{mV/Hz}}.$$

• Da nun aber die Zeitfunktion nur halb so breit ist, verbreitert sich das Spektrum um den Faktor  $2$:

$$Y( {f = 1\;{\rm{kHz}}} ) = Y_0 \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{4}} ) \hspace{0.15 cm}\underline{= 2.293\,{\rm{mV/Hz}}}{\rm{.}}$$

• In der Teilaufgabe  (3)  ist dieser Spektralwert bei der Frequenz  $f = 0.5\,\rm{kHz}$  aufgetreten.