Difference between revisions of "Aufgaben:Exercise 3.4Z: Trapezoid, Rectangle and Triangle"
From LNTwww
| Line 65: | Line 65: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equivalent pulse duration is $\Delta t = t_1 + t_2 \;\underline{= 10 \,\text{ms}}$ and the rolloff factor $r_t = 2/10 \;\underline{= 0.2}$. |
| − | '''(2)''' | + | '''(2)''' Proposed <u>solutions 2 and 3</u> are correct: |
| − | * | + | *The spectral value at $f = 0$ is $A \cdot \Delta t = 10 \,\text{mV/Hz}$. |
| − | * | + | *Since ${X(f)}$ is real and can assume both positive and negative values, only the two phase values $0$ und $\pi$ are possible. |
| − | * | + | *Zeros exist due to the first si-function at all multiples of $1/\Delta t = 100\, \text{Hz}$. |
| − | * | + | *The second si function leads to zero crossings at intervals of $1/(r_t \cdot \Delta t) = 500 \,\text{Hz}$. These coincide exactly with the zeros of the first si-function. |
| − | '''(3)''' <u> | + | '''(3)''' <u>All proposed solutions</u> are correct: |
| − | * | + | *With the equivalent pulse duration $\Delta t = 10 \,\text{ms}$ and the rolloff factor $r_t = 0$ one obtains: $R( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }} \cdot \Delta t \cdot f} ).$ |
| − | * | + | *It follows that $R( f = 0) = A \cdot \Delta t = X( f = 0).$ |
| − | '''(4)''' | + | '''(4)''' Proposed <u>solutions 2 and 3</u> are correct: |
| − | * | + | *For the triangular pulse, the rolloff factor is $r_t = 1$. |
| − | * | + | *The equivalent pulse duration is $\Delta t = 10 \,\text{ms}$. It follows that $D( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }} \cdot \Delta t \cdot f} )$ and $D( f = 0) = A \cdot \Delta t = X( f = 0)$. |
| − | * | + | *Since ${D(f)}$ cannot become negative, the phase $[{\rm arc} \; {D(f)}]$ is always zero. The phase value $\pi$ $(180°)$ is therefore not possible with the triangular form. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:31, 23 January 2021
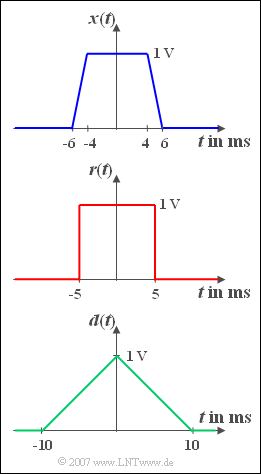
Three different pulse shapes are considered. The pulse ${x(t)}$ is trapezoidal. For $| t | < t_1 = 4 \,\text{ms}$ the time course is constant equal to ${A} = 1\, \text{V}$. Afterwards, ${x(t)}$ drops linearly to the value zero until the time $t_2 = 6\, \text{ms}$ . With the two derived system quantities, namely
- $$\Delta t = t_1 + t_2$$
- and the so-called roll-off factor (in the time domain)
- $$r_t = \frac{t_2 - t_1 }{t_2 + t_1 }$$
is the spectral function of the trapezoidal pulse:
- $$X( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits}( {{\rm \pi} \cdot \Delta t \cdot f} ) \cdot \hspace{0.1cm}{\mathop{\rm si}\nolimits}( {{\rm \pi}\cdot \Delta t \cdot r_t \cdot f} ).$$
Furthermore, the rectangular momentum ${r(t)}$ and the triangular momentum ${d(t)}$ are also shown in the graph, both of which can be interpreted as limiting cases of the trapezoidal momentum ${x(t)}$ .
Hints:
- This exercise belongs to the chapter Fourier Transform Laws.
- You can check your results using the two interactive applets Impulses and Spectra sowie Frequenzgang und Impulsantwort .
Questions
Solution
(1) The equivalent pulse duration is $\Delta t = t_1 + t_2 \;\underline{= 10 \,\text{ms}}$ and the rolloff factor $r_t = 2/10 \;\underline{= 0.2}$.
(2) Proposed solutions 2 and 3 are correct:
- The spectral value at $f = 0$ is $A \cdot \Delta t = 10 \,\text{mV/Hz}$.
- Since ${X(f)}$ is real and can assume both positive and negative values, only the two phase values $0$ und $\pi$ are possible.
- Zeros exist due to the first si-function at all multiples of $1/\Delta t = 100\, \text{Hz}$.
- The second si function leads to zero crossings at intervals of $1/(r_t \cdot \Delta t) = 500 \,\text{Hz}$. These coincide exactly with the zeros of the first si-function.
(3) All proposed solutions are correct:
- With the equivalent pulse duration $\Delta t = 10 \,\text{ms}$ and the rolloff factor $r_t = 0$ one obtains: $R( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }} \cdot \Delta t \cdot f} ).$
- It follows that $R( f = 0) = A \cdot \Delta t = X( f = 0).$
(4) Proposed solutions 2 and 3 are correct:
- For the triangular pulse, the rolloff factor is $r_t = 1$.
- The equivalent pulse duration is $\Delta t = 10 \,\text{ms}$. It follows that $D( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }} \cdot \Delta t \cdot f} )$ and $D( f = 0) = A \cdot \Delta t = X( f = 0)$.
- Since ${D(f)}$ cannot become negative, the phase $[{\rm arc} \; {D(f)}]$ is always zero. The phase value $\pi$ $(180°)$ is therefore not possible with the triangular form.