Difference between revisions of "Aufgaben:Exercise 3.5: Circuit with R, L and C"
m (Text replacement - "Category:Exercises for Linear and Time-Invariant Systems" to "Category:Linear and Time-Invariant Systems: Exercises") |
|||
| (23 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform |
}} | }} | ||
| − | [[File:P_ID1776__LZI_A_3_5.png|right|frame| | + | [[File:P_ID1776__LZI_A_3_5.png|right|frame|Two-port network with $R$, $L$, $C$]] |
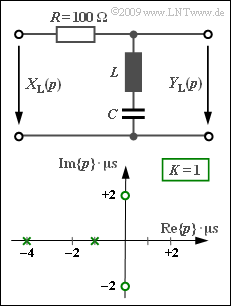
| − | + | We consider a two-port network with the resistance $R = 100 \ \rm \Omega$ in the longitudinal branch, while in the transverse branch an inductance $L$ and a capacitance $C$ are connected in series. The pole–zero diagram is drawn below. | |
| − | + | Note the normalization of the complex frequency $p = {\rm j} \cdot 2 \pi f$ to the value $1/T$ with $T = 1 \ \rm µ s$. As a consequence, for example the pole at $-1$ is at $-10^6 \cdot \ \rm 1/s$ in reality. | |
| − | + | The residue theorem can be applied to compute time functions: | |
| − | * | + | *For $N$ simple poles, the output $y(t)$ is composed of $N$ natural oscillations ("residuals") . |
| − | * | + | *For a simple pole at $p_{{\rm x}i}$, the following holds for the residual: |
:$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} | :$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} | ||
\hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= | \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= | ||
| Line 18: | Line 18: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | : | + | :However, this approach only works if the number $Z$ of zeros is less than $N$. In this exercise, for example if the step response $\sigma(t)$ is computed. In this case, $Z = 2$ and $N = 3$ hold since the step function at the input must additionally be taken into account by $X_{\rm L}(p) = 1/p$ . |
| − | * | + | *This approach does not work for the computation of the impulse response $h(t)$ due to $Z = N =2$ . |
| − | * | + | *Here, the fact that the integral over the impulse response $h(t)$ results in the step response $\sigma(t)$ can be considered. |
| Line 28: | Line 28: | ||
| − | + | Please note: | |
| − | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | |
| − | |||
| − | |||
| − | * | ||
| Line 38: | Line 35: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the function of the two-port network considered here? Is it |
|type="()"} | |type="()"} | ||
| − | - | + | - a low-pass filter, |
| − | - | + | - a high-pass filter, |
| − | - | + | - a band-pass filter, |
| − | + | + | + a band-stop filter? |
| − | { | + | {Compute $L$ and $C$ for the given pole–zero configuration. Consider the normalization value $1/T$ and the resistance $R = 100 \ \rm \Omega$. |
|type="{}"} | |type="{}"} | ||
$L \hspace{0.24cm} = \ $ { 20 3% } $\ \rm µ H$ | $L \hspace{0.24cm} = \ $ { 20 3% } $\ \rm µ H$ | ||
| Line 55: | Line 52: | ||
| − | { | + | {Compute the output signal $y(t) = \sigma(t)$ if a step function $x(t) = \gamma(t)$ is applied to the input. Enter the following signal values: |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { 1 3% } | $y(t = 0) \ = \ $ { 1 3% } | ||
| Line 63: | Line 60: | ||
| − | { | + | {Compute the impulse response $h(t)$ in particular for times $t = 0$ and $t = 1 \ \rm µ s$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $h(t)$ | + | + $h(t)$ includes a Dirac delta function at $t = 0$. |
| − | - | + | - The continuous part of $h(t)$ is negative in the whole range. |
| − | + | + | + The continuous part of $h(t)$ has a maximum. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Suggested solution 4</u> is correct: |
| − | * | + | *At extremely low frequencies $(f \rightarrow 0)$, the capacitance $C$ has infinite resistance and at very high frequencies $(f \rightarrow \infty)$ the inductance $L$. |
| − | *In | + | *In both cases, $Y(f) = X(f)$ ⇒ $H(f) = 1$ holds. |
| − | * | + | *In contrast, the LC series connection acts as a short circuit at the resonance frequency $f_0$ and $H(f = f_0) = 0$ holds. |
| − | * | + | *The followiong follows from the block diagram alone: It is a <u>band-stop filter</u>. |
| − | '''(2)''' | + | '''(2)''' The following $p$–transfer function $($without the normalization factor $1/T)$ is obtained from the pole–zero diagram: |
:$$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot | :$$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot | ||
2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} | 2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The capacitance for the circuit is obtained considering the voltage divider properties with the reactance $p \cdot L$ of the inductance and the reactance $1/(p \cdot C)$ of the capacitance: |
:$$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } | :$$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } | ||
{R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } | {R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } | ||
{p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$ | {p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$ | ||
| − | * | + | *Taking into account the normalization factor $1/T= 10^6 \cdot \rm 1/s$ and by comparison, the following is found: |
:$${R}/{L} \hspace{0.25cm} = \hspace{0.2cm} 5 \cdot 10^{6 }\, {\rm 1/s} | :$${R}/{L} \hspace{0.25cm} = \hspace{0.2cm} 5 \cdot 10^{6 }\, {\rm 1/s} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm | ||
| Line 102: | Line 99: | ||
| − | '''(3)''' | + | '''(3)''' The step function at the input is accounted for by $X_{\rm L}(p) = 1/p$ . This results in |
:$$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} | :$$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} | ||
| − | \hspace{0.05cm} ,$$ | + | \hspace{0.05cm}, $$ |
| − | + | whereof the time function $y(t)$ can be determined by applying the residue theorem: | |
:$$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} | :$$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} | ||
\frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | \frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | ||
| Line 128: | Line 125: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | [[File:P_ID1778__LZI_A_3_5_c.png|right|frame| | + | [[File:P_ID1778__LZI_A_3_5_c.png|right|frame|Step response of the RLC resonant circuit]] |
| − | + | Here, it is taken into account that the constant $10^6 \cdot \rm 1/s$, which is not considered in this calculation, is compensated for by time normalization to $T = 1 \ \rm µ s$. | |
| − | + | The signal values which are looked for are: | |
:$$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, | :$$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, | ||
| Line 138: | Line 135: | ||
\hspace{0.15cm}y(t = 5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.989}\hspace{0.05cm}. $$ | \hspace{0.15cm}y(t = 5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.989}\hspace{0.05cm}. $$ | ||
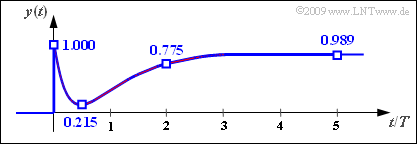
| − | + | The graph shows the signal curve. The searched-for numerical values are inscribed again. | |
| − | + | The following can be seen from this representation: | |
| − | * | + | * Since extremely high frequencies are not affected by the system (band-stop filter), the jump from $0$ to $1$ with infinite edge steepness can also be seen in the output signal $y(t)$. |
| − | + | * The limit of $y(t)$ for $t → \infty$ consequently also yields the value $1$ because of $H(f = 0) = 1$. | |
| − | * | + | * There is a drop in the signal curve due to the LC resonance frequency at $f_0 = 1/\pi$ (in $\rm MHz)$ . |
| − | * | + | *The signal minimum of $\approx 0.215$ is at approximately $t = 0.5 \ \rm µ s$. |
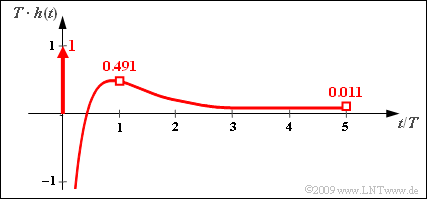
| − | [[File:P_ID1779__LZI_A_3_5_d.png|right|frame| | + | [[File:P_ID1779__LZI_A_3_5_d.png|right|frame|Impulse response of the RLC low-pass filter]] |
| − | '''(4)''' | + | '''(4)''' <u>Suggested solutions 1 and 3</u> are correct: |
| − | * | + | *The impulse response $h(t)$ is obtained from the step response $\sigma(t)=y(t)$ by differentiation: |
:$$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm | :$$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm | ||
d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ | d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ | ||
| Line 155: | Line 152: | ||
\hspace{0.05cm}-4t/T} | \hspace{0.05cm}-4t/T} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The first suggested solution is thus correct since differentiation of a step function $\gamma(t)$ yields the Dirac delta function $\delta(t)$. |
| − | * | + | *The following numerical values are obtained for the continuous part of $h(t)$ : |
:$$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}- {20}/{3}= -5 | :$$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}- {20}/{3}= -5 | ||
\hspace{0.05cm} ,$$ | \hspace{0.05cm} ,$$ | ||
| Line 164: | Line 161: | ||
0.018\approx 0.491 | 0.018\approx 0.491 | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *Since $h(t)$ tends to zero in the limiting case for $t → \infty$, the third proposed solution is also correct in contrast to the second one. |
| − | * | + | *The curve of $h(t)$ is shown in the adjacent diagram. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 171: | Line 168: | ||
| − | [[Category:Linear and Time-Invariant Systems: Exercises|^3.3 | + | [[Category:Linear and Time-Invariant Systems: Exercises|^3.3 Inverse Laplace Transform^]] |
Latest revision as of 11:12, 10 November 2021
We consider a two-port network with the resistance $R = 100 \ \rm \Omega$ in the longitudinal branch, while in the transverse branch an inductance $L$ and a capacitance $C$ are connected in series. The pole–zero diagram is drawn below.
Note the normalization of the complex frequency $p = {\rm j} \cdot 2 \pi f$ to the value $1/T$ with $T = 1 \ \rm µ s$. As a consequence, for example the pole at $-1$ is at $-10^6 \cdot \ \rm 1/s$ in reality.
The residue theorem can be applied to compute time functions:
- For $N$ simple poles, the output $y(t)$ is composed of $N$ natural oscillations ("residuals") .
- For a simple pole at $p_{{\rm x}i}$, the following holds for the residual:
- $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \hspace{0.05cm} .$$
- However, this approach only works if the number $Z$ of zeros is less than $N$. In this exercise, for example if the step response $\sigma(t)$ is computed. In this case, $Z = 2$ and $N = 3$ hold since the step function at the input must additionally be taken into account by $X_{\rm L}(p) = 1/p$ .
- This approach does not work for the computation of the impulse response $h(t)$ due to $Z = N =2$ .
- Here, the fact that the integral over the impulse response $h(t)$ results in the step response $\sigma(t)$ can be considered.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
Questions
Solution
- At extremely low frequencies $(f \rightarrow 0)$, the capacitance $C$ has infinite resistance and at very high frequencies $(f \rightarrow \infty)$ the inductance $L$.
- In both cases, $Y(f) = X(f)$ ⇒ $H(f) = 1$ holds.
- In contrast, the LC series connection acts as a short circuit at the resonance frequency $f_0$ and $H(f = f_0) = 0$ holds.
- The followiong follows from the block diagram alone: It is a band-stop filter.
(2) The following $p$–transfer function $($without the normalization factor $1/T)$ is obtained from the pole–zero diagram:
- $$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot 2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} \hspace{0.05cm} .$$
- The capacitance for the circuit is obtained considering the voltage divider properties with the reactance $p \cdot L$ of the inductance and the reactance $1/(p \cdot C)$ of the capacitance:
- $$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } {R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } {p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$
- Taking into account the normalization factor $1/T= 10^6 \cdot \rm 1/s$ and by comparison, the following is found:
- $${R}/{L} \hspace{0.25cm} = \hspace{0.2cm} 5 \cdot 10^{6 }\, {\rm 1/s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm 1/s}}\hspace{0.15cm}\underline{= 20\,{\rm µ H} \hspace{0.05cm}} ,$$
- $${1}/({LC}) \hspace{0.25cm} = \hspace{0.2cm}4 \cdot 10^{12 }\, {\rm 1/s^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}C= \frac{1}{4 \cdot 10^{12 }\, {\rm 1/s^2}\cdot 2 \cdot 10^{-5 }\, {\rm \Omega \cdot s} } \hspace{0.15cm}\underline{= 12.5\,{\rm nF}} \hspace{0.05cm} .$$
(3) The step function at the input is accounted for by $X_{\rm L}(p) = 1/p$ . This results in
- $$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} \hspace{0.05cm}, $$
whereof the time function $y(t)$ can be determined by applying the residue theorem:
- $$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}0}= 1 \hspace{0.05cm} ,$$
- $$ y_2(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { p\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= - {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-t} \hspace{0.05cm} ,$$
- $$ y_3(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { p\cdot(p +1 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-4}= {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4t}$$
- $$\Rightarrow \hspace{0.3cm}y(t)= y_1(t)+y_2(t)+y_3(t)= 1- {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}+\ {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4t/T} \hspace{0.05cm} .$$
Here, it is taken into account that the constant $10^6 \cdot \rm 1/s$, which is not considered in this calculation, is compensated for by time normalization to $T = 1 \ \rm µ s$.
The signal values which are looked for are:
- $$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, \hspace{0.15cm}y(t = 0.5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.215}\hspace{0.05cm}, $$
- $$y(t = 2\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.775}\hspace{0.05cm}, \hspace{0.15cm}y(t = 5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.989}\hspace{0.05cm}. $$
The graph shows the signal curve. The searched-for numerical values are inscribed again.
The following can be seen from this representation:
- Since extremely high frequencies are not affected by the system (band-stop filter), the jump from $0$ to $1$ with infinite edge steepness can also be seen in the output signal $y(t)$.
- The limit of $y(t)$ for $t → \infty$ consequently also yields the value $1$ because of $H(f = 0) = 1$.
- There is a drop in the signal curve due to the LC resonance frequency at $f_0 = 1/\pi$ (in $\rm MHz)$ .
- The signal minimum of $\approx 0.215$ is at approximately $t = 0.5 \ \rm µ s$.
(4) Suggested solutions 1 and 3 are correct:
- The impulse response $h(t)$ is obtained from the step response $\sigma(t)=y(t)$ by differentiation:
- $$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}- \frac {20}{3T}\cdot {\rm e}^{ \hspace{0.05cm}-4t/T} \hspace{0.05cm} .$$
- The first suggested solution is thus correct since differentiation of a step function $\gamma(t)$ yields the Dirac delta function $\delta(t)$.
- The following numerical values are obtained for the continuous part of $h(t)$ :
- $$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}- {20}/{3}= -5 \hspace{0.05cm} ,$$
- $$ T \cdot h(t = T )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-1}- {20}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4}= {5}/{3}\cdot 0.368- {20}/{3}\cdot 0.018\approx 0.491 \hspace{0.05cm} .$$
- Since $h(t)$ tends to zero in the limiting case for $t → \infty$, the third proposed solution is also correct in contrast to the second one.
- The curve of $h(t)$ is shown in the adjacent diagram.