Difference between revisions of "Aufgaben:Exercise 3.5: Triangular and Trapezoidal Signal"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Uniformly_Distributed_Random_Variables |
}} | }} | ||
| − | [[File:P_ID125__Sto_A_3_5.png|right|frame| | + | [[File:P_ID125__Sto_A_3_5.png|right|frame|rectangle–, triangle– and trapezoid signal ]] |
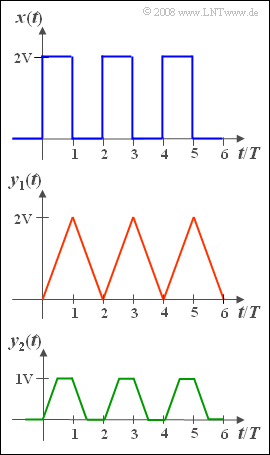
| − | + | We start from the rectangular signal $x(t)$ according to the upper graph. | |
| − | * | + | *The amplitude values are $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$. |
| − | * | + | *Let the duration of a rectangle and the distance between two successive rectangular pulses be equal to each $T$. |
| − | * | + | *The random variable $x$ – the instantaneous value of the rectangular signal $x(t)$ – thus has the following characteristic values: |
:$$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$ | :$$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$ | ||
| − | + | If we now apply this signal to a linear filter with the impulse response | |
| − | :$$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm | + | :$$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T} \\\ 0 & {\rm else} \end{array} \right. , $$ |
| − | + | then the triangular signal $y_1(t) = x(t) \star h_1(t)$ is obtained at its output according to the convolution with | |
| − | * | + | *the minimum values $0\hspace{0.05cm} \rm V$ $($at $t = 0, 2T, 4T,$ ...$)$, |
| − | * | + | *the maximum values $2\hspace{0.05cm} \rm V$ $($bei $t = T, 3T, 5T,$ ...$)$. |
| − | + | Thus, this low-pass filter is an integrator over the time duration $T$.<br> | |
| − | + | If, on the other hand, we apply the signal $x(t)$ to the input of a filter with the impulse response | |
| − | :$$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm | + | :$$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T/2} \\\ 0 & {\rm else} \end{array} \right. , $$ |
| − | so | + | so the trapezoidal signal $y_2(t) = x(t) \star h_2(t)$. This second filter thus acts as an integrator over the time duration $T/2$. |
<br> | <br> | ||
| Line 31: | Line 31: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Uniformly_Distributed_Random_Variables|Uniformly distributed random variables]]. |
| − | * | + | *For the corresponding frequency bands $H_1(f=0)= 1$ or $H_2(f=0)= 0.5$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $y_1(t)$ | + | + $y_1(t)$ is a continuous random variable. |
| − | - $y_1(t)$ | + | - $y_1(t)$ has a triangular PDF. |
| − | + $y_1(t)$ | + | + $y_1(t)$ is uniformly distributed. |
| − | + $y_2(t)$ | + | + $y_2(t)$ has continuous and discrete components. |
| − | { | + | {How large; is the uniform part of the signal $y_1(t)$? &Check this value $m_{y1}$ also by using the variables $m_x$ and $H_1(f=0)$. |
|type="{}"} | |type="{}"} | ||
| − | $m_{y1} \ = \ $ | + | $m_{y1} \ = \ $ { 1 3% } $\ \rm V$ |
| − | { | + | {Determine the power of the signal $y_1(t)$ by both time averaging and coulter averaging. |
|type="{}"} | |type="{}"} | ||
$P_{y1} \ = \ $ { 1.333 3% } $\ \rm V^2$ | $P_{y1} \ = \ $ { 1.333 3% } $\ \rm V^2$ | ||
| − | { | + | {What is the rms of the signal $y_1(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_{y1} \ = \ $ | + | $\sigma_{y1} \ = \ $ { 0.577 3% } $\ \rm V$ |
| − | { | + | {What is the probability that $y_1(t)$ is larger than $0.75\hspace{0.05cm} \rm V$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 62.5 3% } $ \ \%$ | ${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 62.5 3% } $ \ \%$ | ||
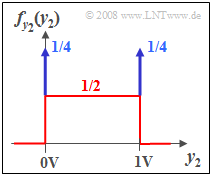
| − | { | + | {Determine the PDF of the signal $y_2(t)$ and sketch it. As a check, enter the PDF value at the point $y_2 = 0.5\hspace{0.05cm} \rm V$ Enter. |
|type="{}"} | |type="{}"} | ||
| − | $f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \ = \ $ | + | $f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \ = \ $ { 0.5 3% } $\ \rm 1/V$ |
| − | { | + | {What is the DC component of the signal $y_2(t)$? &Check this value $m_{y2}$ also using the quantities $m_x$ and $H_2(f=0)$. |
|type="{}"} | |type="{}"} | ||
$m_{y2} \ = \ ${ 0.5 3% } $\ \rm V$ | $m_{y2} \ = \ ${ 0.5 3% } $\ \rm V$ | ||
| − | { | + | {What is the rms value of the signal $y_2(t)$? |
|type="{}"} | |type="{}"} | ||
$\sigma_{y2} \ = \ $ { 0.409 3% } $\ \rm V$ | $\sigma_{y2} \ = \ $ { 0.409 3% } $\ \rm V$ | ||
| − | { | + | {What is the probability that $y_2(t)$ is larger than $0.75\hspace{0.05cm} \rm V$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y_2 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 37.5 3% } $ \ \%$ | ${\rm Pr}(y_2 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 37.5 3% } $ \ \%$ | ||
| Line 91: | Line 91: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solutions=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[File:P_ID121__Sto_A_3_5_a_neu.png|right|frame|Amplitudenbegrenzung, ablesbar in der WDF]] | [[File:P_ID121__Sto_A_3_5_a_neu.png|right|frame|Amplitudenbegrenzung, ablesbar in der WDF]] | ||
Revision as of 01:33, 29 December 2021
We start from the rectangular signal $x(t)$ according to the upper graph.
- The amplitude values are $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$.
- Let the duration of a rectangle and the distance between two successive rectangular pulses be equal to each $T$.
- The random variable $x$ – the instantaneous value of the rectangular signal $x(t)$ – thus has the following characteristic values:
- $$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$
If we now apply this signal to a linear filter with the impulse response
- $$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T} \\\ 0 & {\rm else} \end{array} \right. , $$
then the triangular signal $y_1(t) = x(t) \star h_1(t)$ is obtained at its output according to the convolution with
- the minimum values $0\hspace{0.05cm} \rm V$ $($at $t = 0, 2T, 4T,$ ...$)$,
- the maximum values $2\hspace{0.05cm} \rm V$ $($bei $t = T, 3T, 5T,$ ...$)$.
Thus, this low-pass filter is an integrator over the time duration $T$.
If, on the other hand, we apply the signal $x(t)$ to the input of a filter with the impulse response
- $$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T/2} \\\ 0 & {\rm else} \end{array} \right. , $$
so the trapezoidal signal $y_2(t) = x(t) \star h_2(t)$. This second filter thus acts as an integrator over the time duration $T/2$.
Hints:
- This exercise belongs to the chapter Uniformly distributed random variables.
- For the corresponding frequency bands $H_1(f=0)= 1$ or $H_2(f=0)= 0.5$.
Questions
Solutions
(1) Richtig sind die Lösungsvorschläge 1, 3 und 4:
- Die Zufallsgröße $y_1$ ist gleichverteilt und dadurch ebenso wie $x$ auch eine kontinuierliche Zufallsgröße.
- Die WDF von $y_2$ weist diskrete Anteile bei $0\hspace{0.05cm} \rm V$ und $2\hspace{0.05cm} \rm V$ auf.
- Zwischen diesen zwei Begrenzungen gibt es selbstverständlich auch kontinuierliche Anteile.
- In diesem Bereich gilt $f_{y2}(y_2) = 1/2$.
(2) Der lineare Mittelwert $m_x = 1\hspace{0.05cm} \rm V$ ist aus der Angabenskizze direkt abzulesen, könnte aber auch formal mit der Gleichung für die Gleichverteilung $($zwischen $0\hspace{0.05cm} \rm V$ und $2\hspace{0.05cm} \rm V)$ berechnet werden. Eine weitere Lösungsmöglichkeit bietet die Beziehung:
- $$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 1 \hspace{0.15cm}\underline{ =\rm 1\hspace{0.05cm} \rm V}.$$
(3) Eigentlich müsste die Mittelung über den gesamten Zeitbereich (beidseitig bis ins Unendliche) erfolgen.
- Aus Symmetriegründen genügt jedoch die Mittelung über das Zeitintervall $0 \le t \le T$:
- $$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}{\rm (}\it t{\rm {\rm )}}^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T}{\rm )}^{\rm 2} \hspace{0.1cm}{\rm d} t = \rm {4}/{3}\, V^2 \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$
- Die Scharmittelung liefert das gleiche Ergebnis. Mit der WDF $f_{y1}(y_1) = 1/(2\hspace{0.05cm} \rm V)$ gilt nämlich:
- $$P_{y_{\rm 1}}= \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}{\rm (}\it y_{\rm 1}{\rm )}\it \hspace{0.1cm}{\rm d}y_{\rm 1} =\rm\frac{1}{2V}\cdot \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\hspace{0.1cm}{\rm d}y_{\rm 1} =\rm \frac{8\,{\rm V^3}}{3 \cdot 2\,{\rm V}} \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$
(4) Die Varianz kann mit dem Satz von Steiner ermittelt werden und ergibt
- $$4/3\hspace{0.05cm} \rm V^2 - 1\hspace{0.05cm} \rm V^2 = 1/3\hspace{0.05cm} \rm V^2.$$
- Die Wurzel daraus ist die gesuchte Streuung (der Effektivwert):
- $$\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$$
(5) Die gesuchte Wahrscheinlichkeit ist das Integral über die WDF von $0.75\hspace{0.05cm} \rm V$ bis $2\hspace{0.05cm} \rm V$, also
- $${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{ = 62.5\%}.$$
(6) Die WDF besteht aus zwei Diracfunktionen bei $0\hspace{0.05cm} \rm V$ und $1\hspace{0.05cm} \rm V$ $($jeweils mit dem Gewicht $1/4)$ und einem konstanten kontinuierlichen Anteil von
- $$f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{=0.5 \cdot\rm 1/V}.$$
- Bei $y_2 = 0.5 \hspace{0.05cm} \rm V$ gibt es deshalb nur den kontinuierlichen Anteil.
(7) Der Mittelwert $m_{y_{\rm 2}}\hspace{0.15cm}\underline{ =\rm 0.5\hspace{0.05cm} \rm V}$ kann direkt aus obiger WDF-Skizze abgelesen werden oder wie in der Teilaufgabe (2) wie folgt berechnet werden:
- $$m_{y_{\rm 2}} = m_x\cdot H_{\rm 2}( f = 0) = 1\hspace{0.05cm} \rm V \cdot 0.5 {\hspace{0.1cm} = \rm 0.5\hspace{0.05cm} \rm V}.$$
(8) Mit obiger WDF gilt für die Leistung:
- $$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}{\rm (}\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 = 5/12 \,V^2 \hspace{0.15cm}{ =\rm 0.417\,V^2}.$$
- Der erste Anteil geht auf die kontinuierliche WDF zurück, der zweite auf die WDF–Diracfunktion bei $1\hspace{0.05cm} \rm V$.
- Die Diracfunktion bei $0\hspace{0.05cm} \rm V$ liefert keinen Beitrag zur Leistung. Daraus folgt für den Effektivwert:
- $$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= \sqrt{{\rm 1}/{\rm 6}\rm V^2} \hspace{0.15cm}\underline{=0.409\, \rm V}.$$
(9) Diese Wahrscheinlichkeit setzt sich ebenfalls aus zwei Anteilen zusammen:
- $${\rm Pr}(y_2 > 0.75 {\rm V} ) = {\rm Pr}(0.75 {\rm V} \le y_2 < 1 {\rm V} ) + {\rm Pr}(y_2 = 1 {\rm V} ) = \frac{1}{2} \cdot \frac{1}{4}+ \frac{1}{4} = \frac{3}{8}\hspace{0.15cm}\underline{ = 37.5\%}. $$