Difference between revisions of "Aufgaben:Exercise 3.6Z: Examination Correction"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables |
}} | }} | ||
| − | [[File:P_ID148__Sto_Z_3_6.png|right|frame| | + | [[File:P_ID148__Sto_Z_3_6.png|right|frame|table for ${\rm \phi}(x)$ and ${\rm Q}(x)$]] |
| − | + | In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades: | |
:$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | :$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | ||
| − | + | Further, the exercise must take into account: | |
| − | * | + | *The maximum achievable score is $100$. The best student achieved $88$ points. |
| − | * | + | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function|Gaussian_Distribution]] with mean $m_z = 60$ and rms (standard deviation) $\sigma_z = 10$. |
| − | * | + | *In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation. |
| − | + | For scoring, the guidelines given are: | |
| − | * | + | *Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0". |
| − | * | + | *If one $46\%$ of the total score, one has passed the exam. |
| − | * | + | *The points/grades assignment shall be linear. |
| Line 22: | Line 22: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian distributed random variables]]. |
| − | * | + | *Especially in the school curriculum, the "Gaussian distribution" is often called "normal distribution" This is not quite correct: |
| − | * | + | *A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and rms $\sigma_z = 1$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What criteria should be considered in problem creation so that the score will result in "approximately a normal distribution"? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + There are many exam participants. |
| − | - | + | - The subproblems depend on each other to a large extent. |
| − | + | + | + There are many independent problems. |
| − | - | + | - The exam consists of a single yes/no question. |
| − | { | + | {How many examinees are expected to score "1.0"? |
|type="{}"} | |type="{}"} | ||
$N_\text{1.0} \ = \ $ { 14 3% } | $N_\text{1.0} \ = \ $ { 14 3% } | ||
| − | { | + | {How many examinees are likely to fail the exam? Take into account that $z$ can be taken as a continuous random variable. |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{4.3 ... 5.0} \ = | + | $N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } |
| − | { | + | {Specify the points/grades–assignment. At what point do you get a "3.0"? How many examinees will get this grade? |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{3.0} \ = | + | $N_\text{3.0} \ = \ $ { 159 3% } |
| − | { | + | {How many examinees are expected to receive the grade "2.7"? Justify why exactly that many examinees will receive the grade "3.3". |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{2.7} \ = | + | $N_\text{2.7} \ = \ $ { 146 3% } |
| − | { | + | {What will be the mean grade on this exam? Consider the result of subtask '''(5)''' to solve this subtask. |
|type="{}"} | |type="{}"} | ||
| − | $\rm | + | $\rm mean grade \ = \ $ { 3 3% } |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind <u>die Lösungsvorschläge 1 und 3</u>: | '''(1)''' Richtig sind <u>die Lösungsvorschläge 1 und 3</u>: | ||
Revision as of 21:41, 1 January 2022
In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Further, the exercise must take into account:
- The maximum achievable score is $100$. The best student achieved $88$ points.
- Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a Gaussian_Distribution with mean $m_z = 60$ and rms (standard deviation) $\sigma_z = 10$.
- In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation.
For scoring, the guidelines given are:
- Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0".
- If one $46\%$ of the total score, one has passed the exam.
- The points/grades assignment shall be linear.
Hints:
- The exercise belongs to the chapter Gaussian distributed random variables.
- Especially in the school curriculum, the "Gaussian distribution" is often called "normal distribution" This is not quite correct:
- A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and rms $\sigma_z = 1$.
Questions
Solution
- Nach dem zentralen Grenzwertsatz erhält man für die Summe vieler unabhängiger Größen eine Gaußverteilung.
- Im Umkehrschluss ergibt sich bei nur wenigen und dazu noch abhängigen Aufgaben keine Gaußverteilung.
- Eine einzige Ja/Nein-Frage führt zu einer Zweipunktverteilung $(0$ Punkte oder Maximalpunktzahl$)$.
- Auch bei Einhaltung dieser Gebote wird man bei sehr wenigen Teilnehmern nicht mit einer Gaußverteilung rechnen können.
(2) Man bekommt eine "1.0" mit $82$ Punkten oder mehr.
- Deshalb gilt mit dem Mittelwert $m_z = 60$ und der Streuung $\sigma_z = 10$:
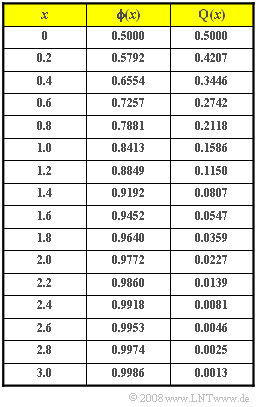
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
- Bei tausend Teilnehmern folgt daraus $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) Mit weniger als $46$ Punkten hat man die Prüfung nicht bestanden:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
- Also müssen wohl 81 Studenten nochmals antreten.
(4) Die Punktedifferenz $82 - 46 = 36$ muss auf neun Notenstufen $(1.3$, ... , $4.0)$ aufgeteilt werden.
- Jedes Intervall umfasst somit $4$ Punkte.
- Beispielsweise erhält man die Note "3.0", wenn man $58$ bis $62$ Punkte erreicht.
- Die Wahrscheinlichkeit, dass die Punktzahl in diesem Bereich liegt, ergibt sich zu
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
Unter Ausnutzung der Symmetrie erhält man:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm Teilnehmer)}.$$
Anmerkungen:
- $z$ ist als kontinuierliche Zufallsgröße aufzufassen. Deshalb ist die Punktzahl $62$ gleichzeitig die obere Grenze für den "3.0"–Bereich als auch die untere Grenze für die Note "2.7" ist.
- Wäre $z$ nur ganzzahlig, so müsste $62$ je nach Stimmung des Korrektors entweder der Note "2.7" oder der Note "3.0" zugeordnet werden. Natürlich müsste das bei allen Prüflingen in gleicher Weise gemacht werden.
(5) Analog zur Musterlösung der Teilaufgabe (4) gilt für die Note "2.7":
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
- Aus Symmetriegründen erhält man für die Note "3.3" den gleichen Wert:
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
- Also erhalten je 146 Teilnehmer die Note "2.7" bzw. "3.3".
(6) Mit der hier getroffenen Punkte–Noten–Zuordnung sind nicht nur die Punkte um $m_z = 60$ symmetrisch verteilt, sondern auch die Noten um „3.0“. Es gibt
- genau so viele „2.7“ wie „3.3“ $($um $±0.3$ von $3.0$ entfernt$)$,
- genau so viele „2.3“ wie „3.7“ $(3.0 ±0.7)$, und
- genau so viele „1.0“ wie „5.0“.
Deshalb ergibt sich die $\rm Mittelnote \hspace{0.15cm}\underline{ 3.0}$.