Difference between revisions of "Aufgaben:Exercise 3.6Z: Examination Correction"
| Line 8: | Line 8: | ||
Further, the exercise must take into account: | Further, the exercise must take into account: | ||
*The maximum achievable score is $100$. The best student achieved $88$ points. | *The maximum achievable score is $100$. The best student achieved $88$ points. | ||
| − | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function| | + | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function|Gaussian distribution]] with mean $m_z = 60$ and rms (standard deviation) $\sigma_z = 10$. |
*In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation. | *In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation. | ||
| Line 32: | Line 32: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What criteria should be considered in problem creation so that the | + | {What criteria should be considered in problem creation so that the grades will result in "approximately a normal distribution"? |
|type="[]"} | |type="[]"} | ||
+ There are many exam participants. | + There are many exam participants. | ||
| Line 62: | Line 62: | ||
{What will be the mean grade on this exam? Consider the result of subtask '''(5)''' to solve this subtask. | {What will be the mean grade on this exam? Consider the result of subtask '''(5)''' to solve this subtask. | ||
|type="{}"} | |type="{}"} | ||
| − | $\rm mean grade \ = \ $ { 3 3% } | + | $\rm mean\hspace{0.15cm}grade \ = \ $ { 3 3% } |
</quiz> | </quiz> | ||
| Line 68: | Line 68: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are <u>the solutions 1 and 3</u>: |
| − | * | + | *According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities. |
| − | * | + | *Conversely, if there are only a few dependent tasks, there is no Gaussian distribution. |
| − | * | + | *A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points). |
| − | * | + | *Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants. |
| − | '''(2)''' | + | '''(2)''' One gets a "1.0" with $82$ points or more. |
| − | * | + | *Therefore, with the mean $m_z = 60$ and the rms $\sigma_z = 10$: |
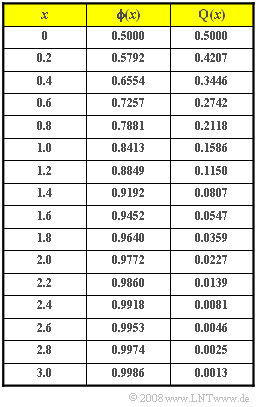
:$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | :$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | ||
\hspace{0.15cm}{=\rm 0.0139}.$$ | \hspace{0.15cm}{=\rm 0.0139}.$$ | ||
| − | * | + | *For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$. |
| − | '''(3)''' | + | '''(3)''' With less than $46$ points, one has failed the exam: |
:$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | :$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | ||
| − | * | + | *So <u>81 students have to compete again</u>. |
| − | '''(4)''' | + | '''(4)''' The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$ . |
| − | * | + | *Each interval thus comprises $4$ points. |
| − | * | + | *For example, one receives a grade of "3.0" if one $58$ to $62$ points. |
| − | * | + | *The probability that the grade is in this range is given by. |
:$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | :$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | ||
| − | + | Taking advantage of the symmetry, one obtains: | |
| − | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm | + | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$ |
| − | '' | + | ''Notes:'' |
| − | *$z$ | + | *$z$ is to be taken as a continuous random variable. Therefore, the score $62$ is simultaneously the upper bound for the "3.0"–range as well as the lower bound for the grade "2.7." |
| − | * | + | *If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector. Of course, this would have to be done in the same way for all examinees. |
| − | '''(5)''' | + | '''(5)''' Analogous to the sample solution of the subtask '''(4)''' applies to the grade "2.7": |
:$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | :$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | ||
| − | * | + | *For reasons of symmetry, the same value is obtained for the grade "3.3": |
:$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | :$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | ||
| − | * | + | *So <u>each 146 participants receive a grade of "2.7" or "3.3"</u>. |
| − | '''(6)''' | + | '''(6)''' With the points–scores–assignment made here, not only are the points distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are |
| − | * | + | *exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$, |
| − | * | + | *exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and |
| − | * | + | *exactly as many "1.0 "s as "5.0 "s. |
| − | + | Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 01:40, 2 January 2022
In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Further, the exercise must take into account:
- The maximum achievable score is $100$. The best student achieved $88$ points.
- Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a Gaussian distribution with mean $m_z = 60$ and rms (standard deviation) $\sigma_z = 10$.
- In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation.
For scoring, the guidelines given are:
- Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0".
- If one $46\%$ of the total score, one has passed the exam.
- The points/grades assignment shall be linear.
Hints:
- The exercise belongs to the chapter Gaussian distributed random variables.
- Especially in the school curriculum, the "Gaussian distribution" is often called "normal distribution" This is not quite correct:
- A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and rms $\sigma_z = 1$.
Questions
Solution
- According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities.
- Conversely, if there are only a few dependent tasks, there is no Gaussian distribution.
- A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points).
- Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants.
(2) One gets a "1.0" with $82$ points or more.
- Therefore, with the mean $m_z = 60$ and the rms $\sigma_z = 10$:
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
- For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) With less than $46$ points, one has failed the exam:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
- So 81 students have to compete again.
(4) The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$ .
- Each interval thus comprises $4$ points.
- For example, one receives a grade of "3.0" if one $58$ to $62$ points.
- The probability that the grade is in this range is given by.
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
Taking advantage of the symmetry, one obtains:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$
Notes:
- $z$ is to be taken as a continuous random variable. Therefore, the score $62$ is simultaneously the upper bound for the "3.0"–range as well as the lower bound for the grade "2.7."
- If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector. Of course, this would have to be done in the same way for all examinees.
(5) Analogous to the sample solution of the subtask (4) applies to the grade "2.7":
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
- For reasons of symmetry, the same value is obtained for the grade "3.3":
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
- So each 146 participants receive a grade of "2.7" or "3.3".
(6) With the points–scores–assignment made here, not only are the points distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are
- exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$,
- exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and
- exactly as many "1.0 "s as "5.0 "s.
Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results.