Difference between revisions of "Aufgaben:Exercise 3.6Z: Examination Correction"
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables |
}} | }} | ||
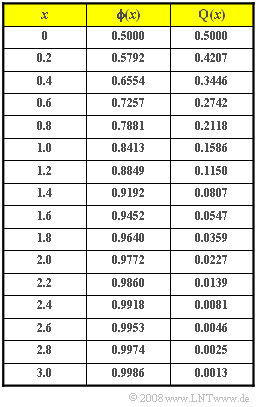
| − | [[File:P_ID148__Sto_Z_3_6.png|right|frame| | + | [[File:P_ID148__Sto_Z_3_6.png|right|frame|Table for ${\rm \phi}(x)$ and ${\rm Q}(x)$]] |
| − | + | In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades: | |
:$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | :$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | ||
| − | + | Further, the exercise must take into account: | |
| − | * | + | *The maximum achievable score is $100$. The best student achieved $88$ points. |
| − | * | + | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – has with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function|Gaussian distribution]] with mean $m_z = 60$ and standard deviation $\sigma_z = 10$. |
| − | * | + | *In the correction,&nbs |
| + | p; not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous valued" with good approximation. | ||
| − | + | For scoring, the guidelines given are: | |
| − | * | + | *Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0". |
| − | * | + | *If one reaches $46\%$ of the total score, one has passed the exam. |
| − | * | + | *The points/grades assignment shall be linear. |
| Line 22: | Line 23: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian distributed random variables]]. |
| − | + | *The "Gaussian distribution" is often called "normal distribution". This is not quite correct: | |
| − | * | + | *A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and standard deviation $\sigma_z = 1$. |
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What criteria should be considered in problem creation so that the grades will result in "approximately a normal distribution"? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + There are many exam participants. |
| − | - | + | - The subproblems depend on each other to a large extent. |
| − | + | + | + There are many independent problems. |
| − | - | + | - The exam consists of a single yes/no question. |
| − | { | + | {How many examinees are expected to score "1.0"? |
|type="{}"} | |type="{}"} | ||
$N_\text{1.0} \ = \ $ { 14 3% } | $N_\text{1.0} \ = \ $ { 14 3% } | ||
| − | { | + | {How many examinees are likely to fail the exam? Take into account that $z$ can be taken as a continuous valued random variable. |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{4.3 ... 5.0} \ = | + | $N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } |
| − | { | + | {Specify the points/grades assignment. At what point do you get a "3.0"? How many examinees will get this grade? |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{3.0} \ = | + | $N_\text{3.0} \ = \ $ { 159 3% } |
| − | { | + | {How many examinees are expected to receive the grade "2.7"? Justify why exactly that many examinees will receive the grade "3.3". |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{2.7} \ = | + | $N_\text{2.7} \ = \ $ { 146 3% } |
| − | { | + | {What will be the mean grade on this exam? Consider the result of subtask '''(5)''' to solve this subtask. |
|type="{}"} | |type="{}"} | ||
| − | $\rm | + | $\rm mean\hspace{0.15cm}grade \ = \ $ { 3 3% } |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are <u>the solutions 1 and 3</u>: |
| − | * | + | *According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities. |
| − | * | + | *Conversely, if there are only a few dependent tasks, there is no Gaussian distribution. |
| − | * | + | *A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points). |
| − | * | + | *Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants. |
| − | '''(2)''' | + | |
| + | '''(2)''' One gets a "1.0" with $82$ points or more. | ||
| + | *Therefore, with the mean $m_z = 60$ and the standard deviation $\sigma_z = 10$: | ||
:$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | :$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | ||
\hspace{0.15cm}{=\rm 0.0139}.$$ | \hspace{0.15cm}{=\rm 0.0139}.$$ | ||
| − | + | *For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$. | |
| + | |||
| − | '''(3)''' | + | '''(3)''' With less than $46$ points, one has failed the exam: |
:$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | :$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | ||
| − | + | *So <u>81 students have to compete again</u>. | |
| + | |||
| − | '''(4)''' | + | '''(4)''' The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$. |
| − | * | + | *Each interval thus comprises $4$ points. |
| − | * | + | *For example, one receives a grade of "3.0" if one has $58$ to $62$ points. |
| − | * | + | *The probability that the grade is in this range is given by |
:$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | :$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | ||
| − | + | *Taking advantage of the symmetry, one obtains: | |
| − | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm | + | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$ |
| − | + | Notes: | |
| − | *$z$ | + | *$z$ is to be taken as a continuous valued random variable. |
| − | * | + | *Therefore, the score $62$ is simultaneously the upper bound for the grade "3.0" as well as the lower bound for the grade "2.7." |
| + | *If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector. | ||
| + | *Of course, this would have to be done in the same way for all examinees. | ||
| − | '''(5)''' | + | |
| + | '''(5)''' Analogous to the solution of the subtask '''(4)''' applies to the grade "2.7": | ||
:$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | :$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | ||
| − | + | *For reasons of symmetry, the same value is obtained for the grade "3.3": | |
:$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | :$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | ||
| − | + | *So <u>each 146 participants receive a grade of "2.7" or "3.3"</u>. | |
| + | |||
| − | '''(6)''' | + | '''(6)''' With the points/grade assignment made here, not only the points are distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are |
| − | * | + | *exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$, |
| − | * | + | *exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and |
| − | * | + | *exactly as many "1.0 "s as "5.0 "s. |
| − | + | Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 123: | Line 130: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.5 Gaussian Random Variable^]] |
Latest revision as of 17:05, 17 February 2022
In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Further, the exercise must take into account:
- The maximum achievable score is $100$. The best student achieved $88$ points.
- Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – has with good approximation a Gaussian distribution with mean $m_z = 60$ and standard deviation $\sigma_z = 10$.
- In the correction,&nbs
p; not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous valued" with good approximation.
For scoring, the guidelines given are:
- Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0".
- If one reaches $46\%$ of the total score, one has passed the exam.
- The points/grades assignment shall be linear.
Hints:
- The exercise belongs to the chapter Gaussian distributed random variables.
- The "Gaussian distribution" is often called "normal distribution". This is not quite correct:
- A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and standard deviation $\sigma_z = 1$.
Questions
Solution
- According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities.
- Conversely, if there are only a few dependent tasks, there is no Gaussian distribution.
- A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points).
- Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants.
(2) One gets a "1.0" with $82$ points or more.
- Therefore, with the mean $m_z = 60$ and the standard deviation $\sigma_z = 10$:
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
- For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) With less than $46$ points, one has failed the exam:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
- So 81 students have to compete again.
(4) The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$.
- Each interval thus comprises $4$ points.
- For example, one receives a grade of "3.0" if one has $58$ to $62$ points.
- The probability that the grade is in this range is given by
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
- Taking advantage of the symmetry, one obtains:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$
Notes:
- $z$ is to be taken as a continuous valued random variable.
- Therefore, the score $62$ is simultaneously the upper bound for the grade "3.0" as well as the lower bound for the grade "2.7."
- If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector.
- Of course, this would have to be done in the same way for all examinees.
(5) Analogous to the solution of the subtask (4) applies to the grade "2.7":
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
- For reasons of symmetry, the same value is obtained for the grade "3.3":
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
- So each 146 participants receive a grade of "2.7" or "3.3".
(6) With the points/grade assignment made here, not only the points are distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are
- exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$,
- exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and
- exactly as many "1.0 "s as "5.0 "s.
Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results.