Difference between revisions of "Aufgaben:Exercise 3.6Z: Two Imaginary Poles"
| Line 60: | Line 60: | ||
+ Für $ \beta > 0$ verläuft $z(t)$ cosinusförmig. | + Für $ \beta > 0$ verläuft $z(t)$ cosinusförmig. | ||
- Für $ \beta > 0$ verläuft $z(t)$ sinusförmig. | - Für $ \beta > 0$ verläuft $z(t)$ sinusförmig. | ||
| − | + Der Grenzfall $\beta → 0$ führt zur Sprungfunktion. | + | + Der Grenzfall $\beta → 0$ führt zur Sprungfunktion $\gamma(t)$. |
| Line 68: | Line 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Durch Anwendung des Residuensatzes erhält man für das Signal $x(t)$ bei positiven Zeiten: | |
| − | + | $$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | |
\hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | ||
\frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | \frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | ||
| − | \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} , | + | \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,$$ |
| − | + | $$ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} | |
\hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | ||
\frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | \frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | ||
| Line 82: | Line 82: | ||
\frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} | \frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | $$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = | |
| − | + | {1}/{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | |
t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | ||
t}\right ] = \cos(2\pi t) | t}\right ] = \cos(2\pi t) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | Richtig sind somit <u>die Lösungsvorschläge 1, 3 und 4</u>. | |
| − | + | ||
| − | + | '''(2)''' Prinzipiell könnte diese Teilaufgabe in gleicher Weise gelöst werden wie die Teilaufgabe (1). Man kann aber auch den Integrationssatz heranziehen. Dieser besagt unter anderem, dass die Multiplikation mit $1p$ im Spektralbereich der Integration im Zeitbereich entspricht: | |
| − | \tau)\,\,{\rm d}\tau = | + | $$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi |
| + | \tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | Richtig sind dementsprechend <u>die Lösungsalternativen 2 und 4</u>. | |
| + | |||
| + | ''Hinweis'': Das kausale Cosinussignal $x(t)$ sowie das hier berechnete kausale Sinussignal $y(t)$ sind auf dem Angabenblatt zu [[Aufgaben:3.6_Einschwingverhalten|Aufgabe 3.6]] als $c_{\rm K}(t)$ bzw. $s_{\rm K}(t)$ dargestellt. | ||
| + | |||
| − | + | '''(3)''' Ein Vergleich mit der Berechnung von $x(t)$ zeigt, dass $z(t) = \cos (\beta \cdot t)$ für $t \ge 0$ und $z(t) = 0$ für $t < 0$0 gilt. Der Grenzübergang für $\beta → 0$ führt damit zur Sprungfunktion $\gamma(t)$ ⇒ <u>Lösungsvorschläge 1 und 3</u>. | |
| − | + | Zum gleichen Ergebnis kommt man durch die Betrachtung im Spektralbereich: | |
| − | + | $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} | |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
z(t) = \gamma(t) | z(t) = \gamma(t) | ||
Revision as of 14:49, 13 February 2017
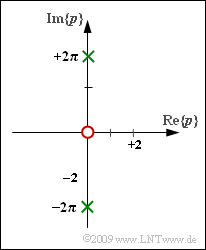
In dieser Aufgabe betrachten wir ein kausales Signal $x(t)$ mit der Laplace–Transformierten $$X_{\rm L}(p) = \frac { p} { p^2 + 4 \pi^2}= \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} \hspace{0.05cm}$$ entsprechend der Grafik (eine rote Nullstelle und zwei grüne Pole).
Das Signal $y(t)$ besitze dagegen die Laplace–Spektralfunktion
- $$Y_{\rm L}(p) = \frac { 1} { p^2 + 4 \pi^2} \hspace{0.05cm}.$$
Die rote Nullstelle gehört somit nicht zu $Y_{\rm L}(p)$.
Abschließend wird noch das Signal $z(t)$ mit der Laplace–Transformierten $$Z_{\rm L}(p) = \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} \hspace{0.05cm}$$ betrachtet, insbesondere der Grenzfall für $\beta → 0$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Frequenzvariable $p$ ist so normiert, dass nach Anwendung des Residuensatzes die Zeit $t$ in Mikrosekunden angegeben ist.
- Ein Ergebnis $t = 1$ ist somit als $t = T$ mit $T = 1 \ \rm \mu s$ zu interpretieren.
- Der Residuensatz lautet am Beispiel der Funktion $X_{\rm L}(p)$ mit zwei einfachen Polstellen bei $ \pm {\rm j} \cdot \beta$:
- $$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \it \beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \it \beta}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(2) Prinzipiell könnte diese Teilaufgabe in gleicher Weise gelöst werden wie die Teilaufgabe (1). Man kann aber auch den Integrationssatz heranziehen. Dieser besagt unter anderem, dass die Multiplikation mit $1p$ im Spektralbereich der Integration im Zeitbereich entspricht:
$$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi
\tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t)
\hspace{0.05cm} .$$
Richtig sind dementsprechend die Lösungsalternativen 2 und 4.
Hinweis: Das kausale Cosinussignal $x(t)$ sowie das hier berechnete kausale Sinussignal $y(t)$ sind auf dem Angabenblatt zu Aufgabe 3.6 als $c_{\rm K}(t)$ bzw. $s_{\rm K}(t)$ dargestellt.
(3) Ein Vergleich mit der Berechnung von $x(t)$ zeigt, dass $z(t) = \cos (\beta \cdot t)$ für $t \ge 0$ und $z(t) = 0$ für $t < 0$0 gilt. Der Grenzübergang für $\beta → 0$ führt damit zur Sprungfunktion $\gamma(t)$ ⇒ Lösungsvorschläge 1 und 3.
Zum gleichen Ergebnis kommt man durch die Betrachtung im Spektralbereich: $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z(t) = \gamma(t) \hspace{0.05cm} .$$