Difference between revisions of "Aufgaben:Exercise 3.7: Impulse Response of a High-Pass Filter"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:EN_LZI_A_3_7.png|right|frame| | + | [[File:EN_LZI_A_3_7.png|right|frame|High-pass filter of second-order]] |
| − | + | We assume the sketched arrangement. The transfer functions of the two identical high-pass filters are: | |
:$$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} | :$$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | Since the two-port networks are decoupled in terms of resistance by an isolation amplifier, the total transfer function can be written as follows: | |
:$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) | :$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | At the same time it is known that the following equation is valid: | |
:$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} | :$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | If this function is represented in pole–zero notation, it will turn out that here the number of zeros $(Z)$ is equal to the number of poles $(N)$ . Therefore, a direct application of the residue theorem is not possible here. | |
| − | + | Instead, in order to compute the time function $h(t)$ a partial fraction decomposition corresponding to | |
$H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) | $H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) | ||
\hspace{0.05cm}$ | \hspace{0.05cm}$ | ||
| − | + | must be made. Thus, the following holds for the impulse response: | |
:$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) | :$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | $Z' < N'$ holds with respect to $H_{\rm L}'(p)$. Thus, the continuous component $h'(t)$ of the impulse response can be determined using the residue theorem. | |
| Line 28: | Line 28: | ||
| − | + | Please note: | |
| − | |||
| − | |||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | ||
| − | + | *The residual of an $l$–fold pole $p_{\rm x}$ within the function $H_{\rm L}(p)$ is: | |
| − | * | ||
:$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | :$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | ||
\hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | \hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | ||
| Line 41: | Line 38: | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The derivative of the product $y(x) = f(x) \cdot g(x)$ is given as follows: |
:$$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm | :$$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm | ||
d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm | d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm | ||
| Line 51: | Line 48: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Represent $H_{\rm L}(p)$ in pole–zero notation. How many zeros $(Z)$ and poles $(N)$ are there? What is the constant factor $K$? |
|type="{}"} | |type="{}"} | ||
$Z \hspace{0.28cm} = \ $ { 2 } | $Z \hspace{0.28cm} = \ $ { 2 } | ||
| Line 58: | Line 55: | ||
| − | { | + | {What is the parameter $A$ of the two partial two-port networks? |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 0.5 3% } | $A \ = \ $ { 0.5 3% } | ||
| − | { | + | {Convert $H_{\rm L}(p) = 1 - H_{\rm L}'(p)$ . What result is obtained for $H_{\rm L}'(p)$? |
| − | |type=" | + | |type="()"} |
- $H_{\rm L}'(p) = p^2/(p+0.5)^2$, | - $H_{\rm L}'(p) = p^2/(p+0.5)^2$, | ||
- $H_{\rm L}'(p) = p/(p+0.5)^2$, | - $H_{\rm L}'(p) = p/(p+0.5)^2$, | ||
| Line 70: | Line 67: | ||
| − | { | + | {Compute the time function $h'(t)$. What are the numerical values for the given times? |
|type="{}"} | |type="{}"} | ||
$h'(t = 0) \ = \ $ { 1 3% } | $h'(t = 0) \ = \ $ { 1 3% } | ||
| Line 82: | Line 79: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Starting from the given equation, $H_{\rm L}(p)$ can be transformed as follows: |
:$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4}=\frac{p^2}{p^2 + p +1/4}=\frac{p^2}{(p +1/2)^2} | :$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4}=\frac{p^2}{p^2 + p +1/4}=\frac{p^2}{(p +1/2)^2} | ||
\hspace{0.3cm} | \hspace{0.3cm} | ||
| Line 91: | Line 88: | ||
| − | '''(2)''' | + | '''(2)''' The total transfer function is as follows according to the information page: |
:$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2} | :$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | A comparison with the result of subtask '''(1)''' shows that $\underline{A = 0.5}$ must hold. | |
| − | '''(3)''' | + | '''(3)''' The <u>last suggested solution</u> is correct: |
| − | * | + | *The following is obtained based on the equation computed in subtask '''(1)''' : |
:$$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p | :$$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p | ||
+0.25}- \frac{p +0.25}{p^2 + p | +0.25}- \frac{p +0.25}{p^2 + p | ||
| Line 109: | Line 106: | ||
| − | '''(4)''' | + | '''(4)''' Concerning the function $H_{\rm L}'(p)$ ⇒ $Z' = 1$, $N' = 2$ and $K' = 1$ hold. |
| − | + | *The two poles at $p_{\rm x} = -0.5$ coincide such that only one residual needs to be determined: | |
:$$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | :$$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | ||
\hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}= | \hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}= | ||
| Line 126: | Line 123: | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | [[File:P_ID1788__LZI_A_3_7_d.png|right|frame| | + | [[File:P_ID1788__LZI_A_3_7_d.png|right|frame|Impulse response of the high-pass filter including Dirac delta (red); <br>continuous component $h\hspace{0.03cm}'(t)$ (blue)]] |
| − | + | *The following is obtained using the product rule of differential calculus: | |
| − | $$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} | + | :$$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} |
{\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | {\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} | ||
| Line 134: | Line 131: | ||
\cdot{\rm e}^{-t/2} | \cdot{\rm e}^{-t/2} | ||
\hspace{0.05cm} $$ | \hspace{0.05cm} $$ | ||
| − | $$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \hspace{0.05cm} ,\hspace{0.3cm} | + | :$$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \hspace{0.05cm} ,\hspace{0.3cm} |
h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$ | h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$ | ||
| − | + | ||
| − | * | + | The graph shows in each case for non–negative times |
| − | * | + | *the impulse response $h'(t)$ of the equivalent low-pass filter as a blue curve, |
| + | *the total impulse response of the considered high-pass filter as a red curve: | ||
:$$h(t) = | :$$h(t) = | ||
\delta (t) - (1- {t}/{4}) | \delta (t) - (1- {t}/{4}) | ||
Latest revision as of 15:21, 25 January 2022
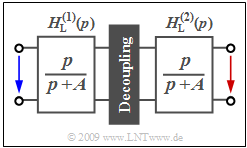
We assume the sketched arrangement. The transfer functions of the two identical high-pass filters are:
- $$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} \hspace{0.05cm} .$$
Since the two-port networks are decoupled in terms of resistance by an isolation amplifier, the total transfer function can be written as follows:
- $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) \hspace{0.05cm} .$$
At the same time it is known that the following equation is valid:
- $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} \hspace{0.05cm} .$$
If this function is represented in pole–zero notation, it will turn out that here the number of zeros $(Z)$ is equal to the number of poles $(N)$ . Therefore, a direct application of the residue theorem is not possible here.
Instead, in order to compute the time function $h(t)$ a partial fraction decomposition corresponding to $H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.05cm}$ must be made. Thus, the following holds for the impulse response:
- $$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm}.$$
$Z' < N'$ holds with respect to $H_{\rm L}'(p)$. Thus, the continuous component $h'(t)$ of the impulse response can be determined using the residue theorem.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
- The residual of an $l$–fold pole $p_{\rm x}$ within the function $H_{\rm L}(p)$ is:
- $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.05cm} .$$
- The derivative of the product $y(x) = f(x) \cdot g(x)$ is given as follows:
- $$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm d}\hspace{0.05cm}x}\cdot f(x) \hspace{0.05cm} .$$
Questions
Solution
- $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4}=\frac{p^2}{p^2 + p +1/4}=\frac{p^2}{(p +1/2)^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{ Z = 2\hspace{0.05cm} , \hspace{0.2cm}N = 2\hspace{0.05cm} , \hspace{0.2cm}K = 1} \hspace{0.05cm} .$$
(2) The total transfer function is as follows according to the information page:
- $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2} \hspace{0.05cm} .$$
A comparison with the result of subtask (1) shows that $\underline{A = 0.5}$ must hold.
(3) The last suggested solution is correct:
- The following is obtained based on the equation computed in subtask (1) :
- $$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p +0.25}- \frac{p +0.25}{p^2 + p +0.25}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{p +0.25}{p^2 + p +0.25}= \frac{p +0.25}{(p +0.5)^2} \hspace{0.05cm} .$$
(4) Concerning the function $H_{\rm L}'(p)$ ⇒ $Z' = 1$, $N' = 2$ and $K' = 1$ hold.
- The two poles at $p_{\rm x} = -0.5$ coincide such that only one residual needs to be determined:
- $$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}= \frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ \frac{p +0.25}{(p +0.5)^2} \cdot (p +0.5)^2 \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} = \hspace{0.2cm}\frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ (p +0.25) \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} \hspace{0.05cm} .$$
- The following is obtained using the product rule of differential calculus:
- $$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} {\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} = \hspace{0.15cm} (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm} $$
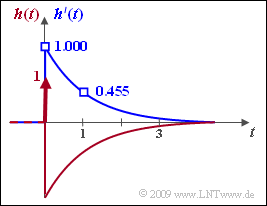
- $$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$
The graph shows in each case for non–negative times
- the impulse response $h'(t)$ of the equivalent low-pass filter as a blue curve,
- the total impulse response of the considered high-pass filter as a red curve:
- $$h(t) = \delta (t) - (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm}.$$