Exercise 3.7Z: Rectangular Signal with Echo
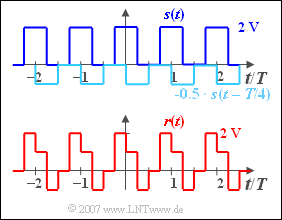
We consider a periodic square wave signal $s(t)$ with the possible amplitude values $0\text{ V}$ and $2\text{ V}$ and the period duration $T_0 = T = 1 \text{ ms}$. At the jump points, for example at $t = T/4$, the signal value is $1\text{ V}$. The DC component $($also i.e. the Fourier coefficient $A_0)$ of the signal is also $1\text{ V}$.
Further applies:
- Due to symmetry (even function), all sine coefficients $B_n = 0$.
- The coefficients $A_n$ with even $n$ are also zero.
- For odd values of $n$ on the other hand, the following applies:
- $$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$
The signal $s(t)$ reaches the receiver via two paths (see sketch below):
- Once on the direct path and secondly via a secondary path.
- The latter is characterised by the attenuation factor $\alpha$ and the transit time $\tau$ .
- Therefore, the following applies to the received signal:
$$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$ The frequency response of the channel is $H(f) = R(f)/S(f)$, the impulse response is denoted by $h(t)$ .
Hints:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
- Important information can be found in particular on the page Convolution of a Function With a Dirac Function.
Questions
Musterlösung
- Die Impulsantwort ist gleich dem Empfangssignal $r(t)$, wenn am Eingang ein einzelner Diracimpuls zum Zeitpunkt $t = 0$ anliegt:
- $$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$
(2) Es gilt $r(t) = s(t) ∗ h(t)$. Diese Faltungsoperation lässt sich am einfachsten grafisch ausführen:
Die Werte des Empfangssignals lauten allgemein:
- $0.00 < t/T < 0.25\text{:}\hspace{0.4cm} r(t) = +1\hspace{0.02cm}\text{ V}$,
- $0.25 < t/T < 0.50\text{:}\hspace{0.4cm} r(t) = -1 \hspace{0.02cm}\text{ V}$,
- $0.50 < t/T < 0.75\text{:}\hspace{0.4cm} r(t) = 0 \hspace{0.02cm}\text{ V}$,
- $0.75 < t/T < 1.00\text{:}\hspace{0.4cm} r(t) = +2 \hspace{0.02cm}\text{ V}$.
Die gesuchten Werte sind somit
- $$r(t = 0.2 \cdot T) \hspace{0.15cm}\underline{= +1 \hspace{0.02cm}\text{ V}},$$
- $$r(t = 0.3 · T) \hspace{0.15cm}\underline{= -1 \hspace{0.02cm}\text{ V}}.$$
(3) Bei ähnlicher Vorgehensweise wie unter (2) erhält man für $r(t)$ ein Gleichsignal von $2 \hspace{0.02cm}\text{ V}$:
- Die Lücken im Signal $s(t)$ werden durch das Echo $s(t - T/2)$ vollständig aufgefüllt.
- Dieses Ergebnis lässt sich auch im Frequenzbereich ableiten.
- Der Kanalfrequenzgang lautet mit $\alpha = 1$ und $\tau = T/2$:
- $$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$
- Das Eingangssignal ${s(t)}$ hat außer dem Gleichanteil nur Anteile bei $f = f_0 = 1/T$, $f = 3 \cdot f_0$, $f = 5 \cdot f_0$ usw..
- Bei diesen Frequenzen sind aber sowohl der Real– als auch der Imaginärteil von ${H(f)}$ gleich Null.
- Damit erhält man für das Ausgangsspektrum mit $A_0 = 1 \text{ V}$ und $H(f = 0) = 2$:
- $$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$
Die Fourierrücktransformation liefert damit ebenfalls $r(t) \underline{= 2 \text{ V= const}}$.