Difference between revisions of "Aufgaben:Exercise 3.7Z: Regenerator Field Length"
| (30 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Linear_Nyquist_Equalization}} |
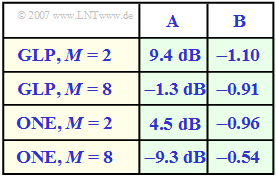
| − | [[File: | + | [[File:EN_Dig_z_3_7.png|right|frame|Results of a system simulation]] |
| − | + | By simulation, it was shown that there is approximately a linear relationship between the so-called "system efficiency" $\eta$ and the "characteristic cable attenuation" $a_*$ of a coaxial cable – both plotted in $\rm dB$ – if the characteristic cable attenuation is sufficiently large $(a_* ≥ 40 \ \rm dB)$: | |
:$$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} | :$$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In the table, the empirically found coefficients $A$ and $B$ are given for four exemplary system variants: |
| − | * | + | * for the intersymbol interference binary system $(M = 2)$ with Gaussian low-pass filter $\rm (GLP)$, see chapter <br>[[Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference|"Error Probability with Intersymbol Interference"]], |
| − | * | + | |
| + | * for the intersymbol interference octal system $(M = 8)$ with Gaussian low-pass filter $\rm (GLP)$, see chapter <br>[[Digital_Signal_Transmission/Intersymbol_Interference_for_Multi-Level_Transmission|"Intersymbol Interference for Multi-Level Transmission"]], | ||
| + | *for optimal ISI–free systems $\rm (ONE)$, see chapter [[Digital_Signal_Transmission/Linear_Nyquist_Equalization|"Linear Nyquist Equalization"]]; $M = 2$ and $M = 8$. | ||
| − | |||
| − | + | The larger the system efficiency $\eta$, the better a system is for a given value $a_*$ (and thus a fixed cable length). | |
| − | + | For the calculation of the '''regenerator field length''' (distance between two repeaters), it should be noted: | |
| − | * | + | * The worst-case error probability should not be larger than $10^{-10}$, which results in the minimum sink SNR: |
| − | :$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_ | + | :$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm |
dB} \hspace{0.05cm},$$ | dB} \hspace{0.05cm},$$ | ||
| − | * | + | * The logarithmized ratio of transmit energy (per bit) and AWGN noise power density is about $100 \ \rm dB$, for example: |
:$$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm | :$$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm | ||
Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$ | Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$ | ||
| Line 27: | Line 28: | ||
\cdot 10^{-9}\,{\rm 1/s}} | \cdot 10^{-9}\,{\rm 1/s}} | ||
= 100\,{\rm | = 100\,{\rm | ||
| − | dB} \hspace{0.05cm} | + | dB} \hspace{0.05cm}.$$ |
| − | * | + | * A standard coaxial cable with dimensions $2.6 \ \rm mm$ (inside) and $9.5 \ \rm mm$ (outside) is to be used, for which the following relationship is valid: |
:$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | :$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | ||
MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | :Here, $a_*$ denotes the characteristic attenuation at half the bit rate – in the example at $500 \ \rm MHz$ – and $l$ denotes the cable length. | |
| + | |||
| − | + | Note: The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Nyquist_Equalization|"Linear Nyquist Equalization"]]. | |
| − | + | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The system $({\rm ONE}, \ M = 8)$ is best for any $a_*$. |
| − | - | + | - The system $({\rm GLP}, \ M = 2)$ is worst for $a_* ≥ 40 \ \rm dB$. |
| + | |||
| + | {Starting from which cable attenuation is the system $({\rm GLP}, \ M = 8)$ better than the system $({\rm ONE}, \ M = 2)$? | ||
| + | |type="{}"} | ||
| + | $a_{\rm *, \ limit}\ = \ $ { 116 3% } $\ \rm dB$ | ||
| − | { | + | {What is the minimum value $\eta_{\hspace{0.05cm}\rm min}$ that the system efficiency must never fall below? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $10 \cdot {\rm lg} \ \eta_{\hspace{0.05cm}\rm min} \ = \ $ { -86.417--81.383 } $\ \rm dB$ |
| + | |||
| + | {What is the maximum length of the coaxial cable for the system $({\rm ONE}, \ M = 8)$? | ||
| + | |type="{}"} | ||
| + | $l_{\hspace{0.05cm}\rm max}\ = \ $ { 2.62 3% } $\ \rm km$ | ||
| + | |||
| + | {What is the maximum length of the coaxial cable for the system $({\rm GTP}, \ M = 2)$? | ||
| + | |type="{}"} | ||
| + | $l_{\hspace{0.05cm}\rm max}\ = \ $ { 1.61 3% } $\ \rm km$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Calculating the system efficiency under the assumption $a_* = 40 \ \rm dB$, we obtain for the four system variants: |
| − | '''(2)''' | + | :$$({\rm GLP},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm} 10 \cdot {\rm |
| − | '''(3)''' | + | lg}\hspace{0.1cm}\eta |
| − | '''(4)''' | + | = +9.4\,{\rm dB} -1.10 \cdot 40\,{\rm dB} = -34.6\,{\rm dB}\hspace{0.05cm},$$ |
| − | '''(5)''' | + | :$$({\rm GLP},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm}10 \cdot {\rm |
| + | lg}\hspace{0.1cm}\eta | ||
| + | = -1.3\,{\rm dB} -0.91 \cdot 40\,{\rm dB} = -37.7\,{\rm dB}\hspace{0.05cm},$$ | ||
| + | :$$({\rm ONE},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm}10 \cdot {\rm | ||
| + | lg}\hspace{0.1cm}\eta | ||
| + | = +4.5\,{\rm dB} -0.96 \cdot 40 \,{\rm dB}= -33.9\,{\rm dB}\hspace{0.05cm},$$ | ||
| + | :$$({\rm ONE},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm} 10 \cdot {\rm | ||
| + | lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot 40\,{\rm dB} = -30.9\,{\rm | ||
| + | dB}\hspace{0.05cm}.$$ | ||
| + | |||
| + | From this it follows: | ||
| + | *The <u>first statement</u> is true because the system $({\rm ONE},\hspace{0.1cm} M = 8)$ is already best at $40 \ \rm dB$ cable attenuation and has the most favorable $\rm B$ coefficient. | ||
| + | |||
| + | *In contrast, the second statement is false because, for example, at $40 \ \rm dB$ cable attenuation, the octal $\rm GLP$ system is worse than the binary one. | ||
| + | |||
| + | |||
| + | '''(2)''' As a determination equation, we use here: | ||
| + | :$$-1.3\,{\rm dB} -0.91 \cdot a_{\star} = +4.5 \,{\rm dB}-0.96 \cdot a_{\star}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} 0.05 \cdot a_{\star} = 5.8\,{\rm dB} | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\star,\hspace{0.05cm}{\rm limit}} \hspace{0.15cm}\underline {= 116\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | That is: | ||
| + | *Up to the characteristic cable attenuation $a_* = 116 \ \rm dB$ $($note: this is an unrealistically large value for currently realized systems$)$, the binary Nyquist system is superior to the system $({\rm GLP},\hspace{0.1cm} M = 8)$. | ||
| + | |||
| + | *Only for larger values than $a_{\rm *, \ limit} = 116 \ \rm dB$ does the advantage of the latter $(M = 8$ and thus significantly lower symbol rate$)$ outweigh the disadvantage $($octal decision and thus greater weight of intersymbol interference$)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The sink SNR should be at least $16.1 \ \rm dB$, which means that it must be valid: | ||
| + | :$$10 \cdot {\rm lg}\hspace{0.1cm}\rho = 10 \cdot {\rm lg} | ||
| + | \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} + 10 \cdot {\rm | ||
| + | lg}\hspace{0.1cm}\eta \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta \ > | ||
| + | \ 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} - 10 \cdot {\rm | ||
| + | lg} | ||
| + | \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} = | ||
| + | \ 16.1- 100\hspace{0.15cm}\underline {= -83.9\,{\rm dB} = 10 \cdot {\rm | ||
| + | lg}\hspace{0.1cm}\eta_{\hspace{0.05cm} \rm min}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' For the system considered here: $10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot a_{\star}.$ | ||
| + | *Thus, from the system efficiency condition ⇒ $10 \cdot {\rm lg} \, \eta > \hspace{0.1cm}–83.9 \ \rm dB $, the characteristic cable attenuation condition is: | ||
| + | :$$a_{\star} < \frac{-83.9\,{\rm dB} + 9.3\,{\rm dB}} {-0.54} \approx | ||
| + | 138.1\,{\rm dB} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *With the given equation | ||
| + | :$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | ||
| + | MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | :thus the maximum cable length ("regenerator field length") can be specified: | ||
| + | :$$l_{\rm max} = \frac{138.1\,{\rm dB} } {2.36\,{\rm dB}/{\rm | ||
| + | km} \cdot \sqrt{\rm MHz})\cdot \sqrt{500\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 2.62\, | ||
| + | {\rm km}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Following the same procedure, but in a more compact notation, results in a smaller "regenerator field length" for this "worse" system: | ||
| + | :$$l_{\rm max} = \frac{-(83.9\,{\rm dB}+A)/B } {2.36\,{\rm dB}/{\rm | ||
| + | km} \cdot \sqrt{500}} = \frac{+(83.9+9.4)/1.10 } {2.36\cdot | ||
| + | \sqrt{500}}\hspace{0.1cm}{\rm km}\hspace{0.15cm}\underline {\approx 1.61\, {\rm km}} | ||
| + | \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^3.5 Linear Nyquist Equalization^]] |
Latest revision as of 16:51, 28 June 2022
By simulation, it was shown that there is approximately a linear relationship between the so-called "system efficiency" $\eta$ and the "characteristic cable attenuation" $a_*$ of a coaxial cable – both plotted in $\rm dB$ – if the characteristic cable attenuation is sufficiently large $(a_* ≥ 40 \ \rm dB)$:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} \hspace{0.05cm}.$$
In the table, the empirically found coefficients $A$ and $B$ are given for four exemplary system variants:
- for the intersymbol interference binary system $(M = 2)$ with Gaussian low-pass filter $\rm (GLP)$, see chapter
"Error Probability with Intersymbol Interference",
- for the intersymbol interference octal system $(M = 8)$ with Gaussian low-pass filter $\rm (GLP)$, see chapter
"Intersymbol Interference for Multi-Level Transmission",
- for optimal ISI–free systems $\rm (ONE)$, see chapter "Linear Nyquist Equalization"; $M = 2$ and $M = 8$.
The larger the system efficiency $\eta$, the better a system is for a given value $a_*$ (and thus a fixed cable length).
For the calculation of the regenerator field length (distance between two repeaters), it should be noted:
- The worst-case error probability should not be larger than $10^{-10}$, which results in the minimum sink SNR:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm dB} \hspace{0.05cm},$$
- The logarithmized ratio of transmit energy (per bit) and AWGN noise power density is about $100 \ \rm dB$, for example:
- $$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}}= 10 \cdot {\rm lg} \hspace{0.1cm} \frac{9\,{\rm V^2} } {9 \cdot 10^{-19}\,{\rm V^2/Hz} \cdot 10^{-9}\,{\rm 1/s}} = 100\,{\rm dB} \hspace{0.05cm}.$$
- A standard coaxial cable with dimensions $2.6 \ \rm mm$ (inside) and $9.5 \ \rm mm$ (outside) is to be used, for which the following relationship is valid:
- $$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} \hspace{0.05cm}.$$
- Here, $a_*$ denotes the characteristic attenuation at half the bit rate – in the example at $500 \ \rm MHz$ – and $l$ denotes the cable length.
Note: The exercise belongs to the chapter "Linear Nyquist Equalization".
Questions
Solution
- $$({\rm GLP},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\eta = +9.4\,{\rm dB} -1.10 \cdot 40\,{\rm dB} = -34.6\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm GLP},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta = -1.3\,{\rm dB} -0.91 \cdot 40\,{\rm dB} = -37.7\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm ONE},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta = +4.5\,{\rm dB} -0.96 \cdot 40 \,{\rm dB}= -33.9\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm ONE},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot 40\,{\rm dB} = -30.9\,{\rm dB}\hspace{0.05cm}.$$
From this it follows:
- The first statement is true because the system $({\rm ONE},\hspace{0.1cm} M = 8)$ is already best at $40 \ \rm dB$ cable attenuation and has the most favorable $\rm B$ coefficient.
- In contrast, the second statement is false because, for example, at $40 \ \rm dB$ cable attenuation, the octal $\rm GLP$ system is worse than the binary one.
(2) As a determination equation, we use here:
- $$-1.3\,{\rm dB} -0.91 \cdot a_{\star} = +4.5 \,{\rm dB}-0.96 \cdot a_{\star}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 0.05 \cdot a_{\star} = 5.8\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\star,\hspace{0.05cm}{\rm limit}} \hspace{0.15cm}\underline {= 116\,{\rm dB}}\hspace{0.05cm}.$$
That is:
- Up to the characteristic cable attenuation $a_* = 116 \ \rm dB$ $($note: this is an unrealistically large value for currently realized systems$)$, the binary Nyquist system is superior to the system $({\rm GLP},\hspace{0.1cm} M = 8)$.
- Only for larger values than $a_{\rm *, \ limit} = 116 \ \rm dB$ does the advantage of the latter $(M = 8$ and thus significantly lower symbol rate$)$ outweigh the disadvantage $($octal decision and thus greater weight of intersymbol interference$)$.
(3) The sink SNR should be at least $16.1 \ \rm dB$, which means that it must be valid:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\rho = 10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} + 10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta \ > \ 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} - 10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} = \ 16.1- 100\hspace{0.15cm}\underline {= -83.9\,{\rm dB} = 10 \cdot {\rm lg}\hspace{0.1cm}\eta_{\hspace{0.05cm} \rm min}}\hspace{0.05cm}.$$
(4) For the system considered here: $10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot a_{\star}.$
- Thus, from the system efficiency condition ⇒ $10 \cdot {\rm lg} \, \eta > \hspace{0.1cm}–83.9 \ \rm dB $, the characteristic cable attenuation condition is:
- $$a_{\star} < \frac{-83.9\,{\rm dB} + 9.3\,{\rm dB}} {-0.54} \approx 138.1\,{\rm dB} \hspace{0.05cm}.$$
- With the given equation
- $$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} \hspace{0.05cm}.$$
- thus the maximum cable length ("regenerator field length") can be specified:
- $$l_{\rm max} = \frac{138.1\,{\rm dB} } {2.36\,{\rm dB}/{\rm km} \cdot \sqrt{\rm MHz})\cdot \sqrt{500\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 2.62\, {\rm km}} \hspace{0.05cm}.$$
(5) Following the same procedure, but in a more compact notation, results in a smaller "regenerator field length" for this "worse" system:
- $$l_{\rm max} = \frac{-(83.9\,{\rm dB}+A)/B } {2.36\,{\rm dB}/{\rm km} \cdot \sqrt{500}} = \frac{+(83.9+9.4)/1.10 } {2.36\cdot \sqrt{500}}\hspace{0.1cm}{\rm km}\hspace{0.15cm}\underline {\approx 1.61\, {\rm km}} \hspace{0.05cm}.$$