Difference between revisions of "Aufgaben:Exercise 3.8Z: Circle (Ring) Area"
m (Guenter verschob die Seite 3.8Z Kreis(ring)fläche nach Aufgabe 3.8: Kreis(ring)fläche) |
|||
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables |
}} | }} | ||
| − | [[File:P_ID133__Sto_Z_3_8.png|right| | + | [[File:P_ID133__Sto_Z_3_8.png|right|frame|About the circular ring area]] |
| − | + | We consider circles of different sizes: | |
| − | * | + | *The radius $r$ and the area $A$ can be thought of as interdependent random variables. |
| − | * | + | *It is assumed that the radius is restricted to the area $6 \le r \le 8$ . |
| − | |||
| − | |||
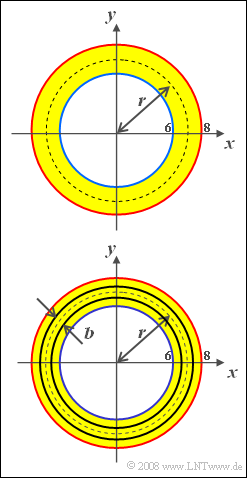
| − | + | In the sketch above, the area in which such circles $($all with center at coordinate origin$)$ can lie is marked in yellow. Furthermore, it can be assumed that the radius in this interval is uniformly distributed: | |
| − | + | :$$f_r(r)=\left\{ \begin{array}{*{4}{c}} 0.5 & \rm for\hspace{0.2cm}{\rm 6\le \it r \le \rm 8}, \\\rm 0 & \rm else. \end{array} \right.$$ | |
| − | |||
| − | '' | + | From subtask '''(5)''' narrow circular rings with center radius $r$ and width $b$ are considered $($lower sketch$)$: |
| − | * | + | *The area of such a circular ring is denoted by $R$. |
| − | * | + | *The possible center radii $r$ are again uniformly distributed between $6$ and $8$. |
| − | + | *The circular ring width is $b = 0.1$. | |
| − | === | + | |
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables|Exponentially distributed random variables]]. | ||
| + | *In particular, reference is made to the page [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|Transformation of random variables]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the transformation characteristic curve $A = g(r)$ analytically. What is the minimum value of the random variable $A$? |
|type="{}"} | |type="{}"} | ||
| − | $A_\text{min} \ = $ { 113.09 3% } | + | $A_\text{min} \ = \ $ { 113.09 3% } |
| − | { | + | {What is the maximum value of the random variable $A$? |
|type="{}"} | |type="{}"} | ||
| − | $A_\text{max} \ = $ { 201.06 3% } | + | $A_\text{max} \ = \ $ { 201.06 3% } |
| − | { | + | {What value $m_{A} = {\rm E}\big[A\big]$ results for the "mean" circular area? |
|type="{}"} | |type="{}"} | ||
| − | $m_{ A} \ = $ { 154.98 3% } | + | $m_{ A} \ = \ $ { 154.98 3% } |
| − | { | + | {Calculate the probability density function of the random variable $A$. What is the probability that the area $A> 150$ ? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(A > 150) \ = $ { | + | ${\rm Pr}(A > 150) \ = \ $ { 54.5 3% } $\ \%$ |
| − | { | + | {What is the PDF of the random variable $R$ $($area of the circular rings according to the sketch below$)$? What is its minimum value? Let $b = 0.1$. |
|type="{}"} | |type="{}"} | ||
| − | + | $R_\text{min} \ = \ $ { 3.77 3% } | |
| − | { | + | {It continues to apply $b = 0.1$. What is the maximum value of the random variable $R$? |
|type="{}"} | |type="{}"} | ||
| − | + | $R_\text{max} \ = \ $ { 5.03 3% } | |
| − | { | + | {What is the expected value of the random variable $R$ for $b = 0.1$? |
|type="{}"} | |type="{}"} | ||
| − | + | ${\rm E}\big[R\big] \ = \ $ { 4.4 3% } | |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equation of the circular area is at the same time the transformation characteristic: $A = \pi \cdot r^2$. |
| + | *From this, with $r = 6$ for the minimum value: | ||
| + | :$$A_\text{min} \hspace{0.15cm}\underline {= 113.09}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Correspondingly, with $r = 8$ for the maximum value: |
| + | :$$A_\text{max} \hspace{0.15cm}\underline {= 201.06}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The simplest way to solve this problem is as follows: |
| − | $$m_{A}={\rm E}[A]={\rm E}[g(r)]=\int_{ -\infty}^{+\infty}g(r)\cdot f_r(r) {\rm d}r.$$ | + | :$$m_{\rm A}={\rm E}\big[A\big]={\rm E}\big[g(r)\big]=\int_{ -\infty}^{+\infty}g(r)\cdot f_r(r) {\rm d}r.$$ |
| − | + | *With $g(r) = \pi \cdot r^2$ and $f_r(r) = 1/2$ in the range of $6$ ... $8$ obtains: | |
| − | $$m_{A}=\int_{\rm 6}^{\rm 8}1/2 \cdot\pi\cdot r^{\rm 2}\, {\rm d} \it r=\frac{\pi}{\rm 6}\cdot \rm ( 8^3-6^3) | + | :$$m_{\rm A}=\int_{\rm 6}^{\rm 8}1/2 \cdot\pi\cdot r^{\rm 2}\, {\rm d} \it r=\frac{\pi}{\rm 6}\cdot \rm ( 8^3-6^3) |
\hspace{0.15cm}\underline{=\rm 154.98}.$$ | \hspace{0.15cm}\underline{=\rm 154.98}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The PDF of the transformed random variable $A$ is: |
| − | $$f_A(A)=\frac{f_r(r)}{|g'(r)|}\Bigg|_{r=h(y) = \sqrt{A/ \pi }}.$$ | + | :$$f_A(A)=\frac{f_r(r)}{|g\hspace{0.05cm}'(r)|}\Bigg|_{r=h(y) = \sqrt{A/ \pi }}.$$ |
| + | |||
| + | *In the range between $A_\text{min} {= 113.09}$ and $A_\text{max} {= 201.06}$ then holds: | ||
| + | :$$f_A(A)=\frac{\rm 1/2}{\rm 2\cdot \pi\cdot\it r}\Bigg|_{\it r=\sqrt{\it A/\rm \pi}}=\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}}.$$ | ||
| − | + | *The probability we are looking for is obtained by integration: | |
| − | + | :$${\rm Pr}(A> 150)=\int_{\rm 150}^{\it A_{\rm max}}\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}} \; \rm d \it A= \frac{\rm 2\cdot\sqrt{\it A}}{\rm 4\cdot\sqrt{\pi}}\Big|_{\rm 150}^{\it A_{\rm max}}.$$ | |
| − | + | *The upper limit of integration yields the value $4$ and the lower limit $3.455$. This yields the probability we are looking for: | |
| − | $${\rm Pr}(A> 150) | + | :$${\rm Pr}(A> 150) \hspace{0.15cm}\underline {=54.5\%}.$$ |
| − | |||
| + | '''(5)''' For the circular ring area $R$ holds for a given radius $r$: | ||
| + | :$$R=\left (r+{b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi-\left ({\it r}-{\it b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi= \rm2\cdot\pi\cdot\it r \cdot b.$$ | ||
| − | + | *There is thus a linear relationship between $R$ and $r$ . | |
| − | $$ | + | *That is: $R$ is also uniformly distributed independently of the width $b$ as long as $b \ll r$. |
| + | *For the minimum value holds: | ||
| + | :$$R_{\rm min}=\rm 2\pi\cdot 6\cdot 0.1\hspace{0.15cm}\underline{\approx3.77}. $$ | ||
| − | |||
| − | |||
| − | '''(6)''' | + | '''(6)''' Accordingly, the maximum value is: |
| − | $$R_{\rm max}=\rm 2\pi\cdot 8\cdot 0.1\hspace{0.15cm}\underline{\approx 5.03}.$$ | + | :$$R_{\rm max}=\rm 2\pi\cdot 8\cdot 0.1\hspace{0.15cm}\underline{\approx 5.03}.$$ |
| − | |||
| − | |||
| + | '''(7)''' Due to the linear relationship between $R$ and $r$ the mean radius $r = 7$ also leads to the mean circular ring area: | ||
| + | :$${\rm E}\big[R\big]=\rm 2\pi\cdot 7\cdot 0.1\hspace{0.15cm}\underline{\approx 4.4}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.6 Exponentially Distributed Random Variables^]] |
Latest revision as of 16:03, 2 February 2022
We consider circles of different sizes:
- The radius $r$ and the area $A$ can be thought of as interdependent random variables.
- It is assumed that the radius is restricted to the area $6 \le r \le 8$ .
In the sketch above, the area in which such circles $($all with center at coordinate origin$)$ can lie is marked in yellow. Furthermore, it can be assumed that the radius in this interval is uniformly distributed:
- $$f_r(r)=\left\{ \begin{array}{*{4}{c}} 0.5 & \rm for\hspace{0.2cm}{\rm 6\le \it r \le \rm 8}, \\\rm 0 & \rm else. \end{array} \right.$$
From subtask (5) narrow circular rings with center radius $r$ and width $b$ are considered $($lower sketch$)$:
- The area of such a circular ring is denoted by $R$.
- The possible center radii $r$ are again uniformly distributed between $6$ and $8$.
- The circular ring width is $b = 0.1$.
Hints:
- The exercise belongs to the chapter Exponentially distributed random variables.
- In particular, reference is made to the page Transformation of random variables.
Questions
Solution
- From this, with $r = 6$ for the minimum value:
- $$A_\text{min} \hspace{0.15cm}\underline {= 113.09}.$$
(2) Correspondingly, with $r = 8$ for the maximum value:
- $$A_\text{max} \hspace{0.15cm}\underline {= 201.06}.$$
(3) The simplest way to solve this problem is as follows:
- $$m_{\rm A}={\rm E}\big[A\big]={\rm E}\big[g(r)\big]=\int_{ -\infty}^{+\infty}g(r)\cdot f_r(r) {\rm d}r.$$
- With $g(r) = \pi \cdot r^2$ and $f_r(r) = 1/2$ in the range of $6$ ... $8$ obtains:
- $$m_{\rm A}=\int_{\rm 6}^{\rm 8}1/2 \cdot\pi\cdot r^{\rm 2}\, {\rm d} \it r=\frac{\pi}{\rm 6}\cdot \rm ( 8^3-6^3) \hspace{0.15cm}\underline{=\rm 154.98}.$$
(4) The PDF of the transformed random variable $A$ is:
- $$f_A(A)=\frac{f_r(r)}{|g\hspace{0.05cm}'(r)|}\Bigg|_{r=h(y) = \sqrt{A/ \pi }}.$$
- In the range between $A_\text{min} {= 113.09}$ and $A_\text{max} {= 201.06}$ then holds:
- $$f_A(A)=\frac{\rm 1/2}{\rm 2\cdot \pi\cdot\it r}\Bigg|_{\it r=\sqrt{\it A/\rm \pi}}=\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}}.$$
- The probability we are looking for is obtained by integration:
- $${\rm Pr}(A> 150)=\int_{\rm 150}^{\it A_{\rm max}}\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}} \; \rm d \it A= \frac{\rm 2\cdot\sqrt{\it A}}{\rm 4\cdot\sqrt{\pi}}\Big|_{\rm 150}^{\it A_{\rm max}}.$$
- The upper limit of integration yields the value $4$ and the lower limit $3.455$. This yields the probability we are looking for:
- $${\rm Pr}(A> 150) \hspace{0.15cm}\underline {=54.5\%}.$$
(5) For the circular ring area $R$ holds for a given radius $r$:
- $$R=\left (r+{b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi-\left ({\it r}-{\it b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi= \rm2\cdot\pi\cdot\it r \cdot b.$$
- There is thus a linear relationship between $R$ and $r$ .
- That is: $R$ is also uniformly distributed independently of the width $b$ as long as $b \ll r$.
- For the minimum value holds:
- $$R_{\rm min}=\rm 2\pi\cdot 6\cdot 0.1\hspace{0.15cm}\underline{\approx3.77}. $$
(6) Accordingly, the maximum value is:
- $$R_{\rm max}=\rm 2\pi\cdot 8\cdot 0.1\hspace{0.15cm}\underline{\approx 5.03}.$$
(7) Due to the linear relationship between $R$ and $r$ the mean radius $r = 7$ also leads to the mean circular ring area:
- $${\rm E}\big[R\big]=\rm 2\pi\cdot 7\cdot 0.1\hspace{0.15cm}\underline{\approx 4.4}.$$