Aufgaben:Exercise 3.8Z: Convolution of Two Rectangles

• Return to book

For the convolution of two rectangles

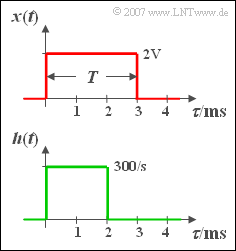
At the input of a causal LTI system (i.e. linear and time-invariant) with a rectangular impulse response  ${h(t)}$  of duration  $2 \,\text{ms}$ , a rectangular impulse  ${x(t)}$  of duration  $T = 3 \,\text{ms}$  and amplitude  $A = 2\,\text{ V}$  is applied. The square-wave functions each start at the time  $t = 0$.

In this task you are to calculate the output signal  ${y(t)}$  with the help of the graphic convolution. As you can easily check, the output signal  ${y(t)}$

• differs from zero only in the range from  $0$  to  $5 \, \text{ms}$  and
• is symmetrical at the time  $t = 2.5 \, \text{ms}$.

Hinweise:

• This exercise belongs to the chapter  The Convolution Theorem and Operation.
• It mainly refers to the page  Graphical Convolution
• The topic of this section is also illustrated in the interactive applet  To illustrate the graphical convolution veranschaulicht.

Questions

1

Calculate the signal values at the times   $t = 1 \,\text{ms}$  and  $t = 2 \,\text{ms}$.

$y(t = 1 \,\text{ms})\ = \ $  $\text{V}$

$y(t = 2 \,\text{ms})\ = \ $  $\text{V}$

2

Determine the signal values for the time points  $t = 3 \,\text{ms}$  and  $t = 4 \,\text{ms}$  by exploiting the symmetry properties.

$y(t = 3 \,\text{ms})\ = \ $  $\text{V}$

$y(t = 4 \,\text{ms})\ = \ $  $\text{V}$

3

Which of the following statements are true?

	The output signal  ${y(t)}$  has a trapezoidal shape.
	The spectrum is:   ${Y(f)} = Y_0 \cdot \text{si}^{2}(\pi f T)$.
	With  $T = 2 \,\text{ms}$ , a triangular shape would result.

Solution

Solution

To illustrate the graphical convolution $x(t) \star h(t)$

(1)  In general, the following applies to the convolution integral:

$$y(t) = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot h( {t - \tau } )}\hspace{0.1cm} {\rm d}\tau.$$

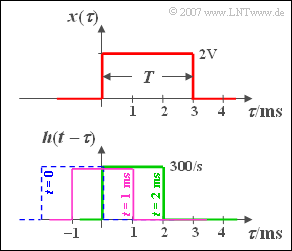
Hints:  The abscissas in the graph opposite have been renamed  $\tau$ .

The signal value at time  $t = 1 \,\text{ms}$  ms can be calculated as follows:

• Reflection of the impulse response  ${h(\tau)}$,
• shift by  $t = 1 \text{ ms}$  to the right (violet curve in the sketch),
• multiplication of the two functions and integration.

The product is also rectangular with the height  $2 \text{ V} \cdot 300 \; \text{1/s}$  and width  $1 \,\text{ms}$. This results in for the area:

$$y( {t = 1\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= 0.6\;{\rm{V}}}{\rm{.}}$$

The green rectangle illustrates the calculation of the second signal value. Now the resulting rectangle is twice as wide after the multiplication and we get:

$$y( {t = 2\;{\rm{ms}}} ) = 2\;{\rm{V}} \cdot {\rm{300}}\;{1}/{{\rm{s}}} \cdot 2\;{\rm{ms}}\hspace{0.15 cm}\underline{={\rm{1.2}}\;{\rm{V}}}{\rm{.}}$$

(2)  Because of the symmetry of ${y(t)}$ with respect to the time  $t = 2.5\, \text {ms}$  holds:

$$y( {t = 3\;{\rm{ms}}} ) = y( {t = 2\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= {\rm{1}}{\rm{.2}}\;{\rm{V}}}{\rm{,}}$$

$$y( {t = 4\;{\rm{ms}}} ) = y( {t = 1\;{\rm{ms}}} )\hspace{0.15 cm}\underline{ = 0.6\;{\rm{V}}}{\rm{.}}$$

Convolution result  $y(t)$

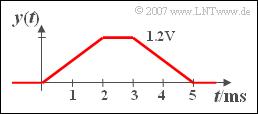
(3)  In subtasks  (1)  and  (2)  the signal values were calculated at discrete time points.

• All points are to be connected by straight line segments, since the integration over rectangular functions of increasing width results in a linear course.
• This means:  The output signal  ${y(t)}$  is trapezoidal.

• The associated spectrum is complex and reads:

$$Y(f) = 6 \cdot 10^{ - 3} \;{{\rm{V}}}/{{{\rm{Hz}}}} \cdot {\mathop{\rm si}\nolimits} ( {2\;{\rm{ms}}\cdot{\rm{\pi }}f} ) \cdot {\mathop{\rm si}\nolimits} ( {3\;{\rm{ms}}\cdot{\rm{\pi }}f}) \cdot {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \hspace{0.05cm}\cdot \hspace{0.05cm}2.5\;{\rm{ms}}\hspace{0.05cm}\cdot \hspace{0.05cm} \pi }}f} .$$

• If the input pulse  ${x(t)}$  had the duration  $T = 2\, \text {ms}$, had the duration  ${y(t)}$  would show a triangular waveform between  ${t = 0}$  and  $t = 4 \text { ms}$ .
• The maximum  $1.2 \, \text {V}$  would then only result at the time  $t = 2 \, \text {ms}$.

Proposed solutions 1 and 3 are therefore correct.