Difference between revisions of "Aufgaben:Exercise 3.9: Convolution of Rectangle and Gaussian Pulse"
| Line 42: | Line 42: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the signa $y_1(t) = x_1(t) \ast h(t)$. <br>What values result at times $t = 0$ und $t = 20\,\text{ns}$ with the approximation $(2\pi )^{1/2} \approx 2.5$? |
|type="{}"} | |type="{}"} | ||
$y_1(t=0)\ = \ $ { 0.682 3% } $\text{V}$ | $y_1(t=0)\ = \ $ { 0.682 3% } $\text{V}$ | ||
$y_1(t=20\,\text{ns})\ = \ $ { 0.158 3% } $\text{V}$ | $y_1(t=20\,\text{ns})\ = \ $ { 0.158 3% } $\text{V}$ | ||
| − | { | + | {What are the signal values of the output signal $y_2(t) = x_2(t) \ast h(t)$ at the points in time considered? |
|type="{}"} | |type="{}"} | ||
$y_2(t=0)\ = \ $ { 0.8 3% } $\text{V}$ | $y_2(t=0)\ = \ $ { 0.8 3% } $\text{V}$ | ||
$y_2(t=20 \,\text{ns})\ = \ $ { 0.11 3% } $\text{V}$ | $y_2(t=20 \,\text{ns})\ = \ $ { 0.11 3% } $\text{V}$ | ||
| − | { | + | {What is the magnitude of the output signa $y_3(t) = x_3(t) \ast h(t)$ at the points in time considered? Interpret the result. |
|type="{}"} | |type="{}"} | ||
$y_3(t=0)\ = \ $ { 0.8 3% } $\text{V}$ | $y_3(t=0)\ = \ $ { 0.8 3% } $\text{V}$ | ||
| Line 61: | Line 61: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The convolution integral here is: |
:$$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$ | :$$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$ | ||
| − | * | + | *Here the substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ was used. The integration limits are at: |
:$$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$ | :$$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$ | ||
| − | * | + | *Using the complementary Gaussian error integral, it is also possible to write for this: |
:$$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$ | :$$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$ | ||
| − | * | + | *For time $t = 0$ one obtains with $(2\pi )^{1/2} \approx 2.5$: |
:$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ | :$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ | ||
| − | * | + | *With $u_1 = -u_2 = -1$ , it follows for the two signal values we are looking for: |
:$$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$ | :$$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$ | ||
| Line 85: | Line 85: | ||
| − | '''(2)''' | + | '''(2)''' Analogous to the first sample solution, one obtains $x_2(t)$ for the narrower input pulse: |
:$$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$ | :$$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$ | ||
Revision as of 23:39, 28 January 2021
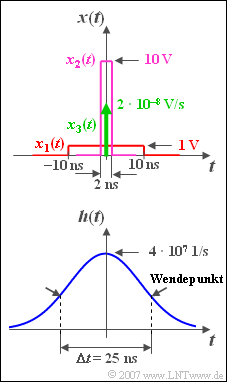
We consider a Gaussian low pass with the equivalent bandwidth $\Delta f = 40 \,\text{MHz}$:
- $$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$
The corresponding impulse response is:
- $$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$
From the sketch it can be seen that the equivalent time duration ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ the impulse response $h(t)$ can be read at the two inflection points of the Gaussian function.
Three different pulse-like signals are now applied to the input of the low-pass filter:
- a square-wave pulse $x_1(t)$ with amplitude $A_1 =1\,\text{V}$ and duration $T_1 = 20\,\text{ns}$ (red curve),
- a rectangular pulse $x_2(t)$ with amplitude $A_2 =10\,\text{V}$ and duration $T_2 = 2\,\text{ns}$ (violet curve),
- a Dirac pulse $x_3(t)$ with pulse weight $2 \cdot 10^{–8}\text{ Vs}$ (green arrow).
Hints:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
- To answer the questions, you can use the complementary Gaussian error integral, which is defined as follows:
- $${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$
This table gives some function values.
Questions
Solution
- $$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$
- Here the substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ was used. The integration limits are at:
- $$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$
- Using the complementary Gaussian error integral, it is also possible to write for this:
- $$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$
- For time $t = 0$ one obtains with $(2\pi )^{1/2} \approx 2.5$:
- $$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$
- With $u_1 = -u_2 = -1$ , it follows for the two signal values we are looking for:
- $$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$
- $$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \big[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \big] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$
(2) Analogous to the first sample solution, one obtains $x_2(t)$ for the narrower input pulse:
- $$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$
- $$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \big[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \big] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$
(3) Beim diracförmigen Eingangssignal $x_3(t)$ ist das Ausgangssignal $y_3(t)$ gleich der Impulsantwort $h(t)$, gewichtet mit dem Gewicht der Diracfunktion:
- $$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$
- Zum Zeitpunkt $t = 0$ erhält man auch hier mit guter Näherung $y_3( t=0)\hspace{0.15 cm}\underline{ =0.8\, {\rm V}}$.
- Nach $20\, \rm ns$ ist der Ausgangsimpuls um den Faktor ${\rm e}^{–0.64π} \hspace{0.15 cm}\underline{\approx 0.136}$ kleiner und man erhält $y_3( t = 20 \,\text{ns}) ≈ 0.11 \,\text{V}$.
Man erkennt aus dem Vergleich der Resultate aus (2) und (3), dass $y_3(t)$ ≈ $y_2(t)$ gilt.
- Der Grund hierfür ist, dass der Diracimpuls eine gute Näherung für einen rechteckförmigen Eingangsimpuls gleicher Fläche ist, wenn die Rechteckdauer $T$ deutlich kleiner als die äquivalente Impulsdauer $\Delta t$ der Impulsantwort ist.
- Das heißt für unser Beispiel: Ist die Dauer $T$ des rechteckförmigen Eingangsimpulses $x(t)$ deutlich kleiner als die äquivalente Dauer $\Delta t$ der gaußförmigen Impulsantwort $h(t)$, dann ist auch der Ausgangsimpuls $y(t)$ nahezu gaußförmig. Aber: Gauß (einmal) gefaltet mit Nicht–Gauß ergibt nie (exakt) Gauß!