Difference between revisions of "Aufgaben:Exercise 3.9Z: Sine Transformation"
| (27 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables |
}} | }} | ||
| − | [[File:P_ID137__Sto_Z_3_9.png|right| | + | [[File:P_ID137__Sto_Z_3_9.png|right|frame|Input PDF, characteristic curve]] |
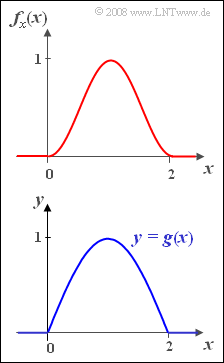
| − | + | In this task, we consider a random variable $x$ with sine-square shaped $\rm PDF$ in the range between $x= 0$ and $x= 2$: | |
| − | $$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot | + | :$$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm for\hspace{0.25cm}{\rm 0\le \it x \le \rm 2} .$$ |
| − | + | Outside of this, the PDF is identically zero. | |
| − | |||
| − | + | The mean and the standard deviation of this random variable $x$ have already been determined in the [[Aufgaben:Exercise_3.3:_Moments_for_cos²-PDF|Exercise 3.3]]: | |
| − | $$ | + | :$$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$ |
| − | + | Another random variable is obtained by transformation using the nonlinear characteristic curve | |
| − | + | :$$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$ | |
| − | |||
| + | The figure shows in each case in the range $0 \le x \le 2$: | ||
| + | *above the PDF $f_x(x)$, | ||
| + | *below the nonlinear characteristic $y = g(x)$. | ||
| − | + | ||
| − | * | + | |
| − | * | + | |
| − | + | ||
| − | * | + | |
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables|Exponentially Distributed Random Variables]]. | ||
| + | *In particular, reference is made to the section [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|"Transformation of random variables"]] and the chapter [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|"Expected Values and Moments"]]. | ||
| + | |||
| + | *Given are the two indefinite integrals: | ||
:$$\int \sin^{\rm 3}( ax)\,{\rm d}x = \frac{\rm 1}{ 3 a} \cdot \cos^{\rm 3}( ax)-\frac{\rm 1}{ a}\cdot \cos(ax),$$ | :$$\int \sin^{\rm 3}( ax)\,{\rm d}x = \frac{\rm 1}{ 3 a} \cdot \cos^{\rm 3}( ax)-\frac{\rm 1}{ a}\cdot \cos(ax),$$ | ||
:$$\int \sin^{\rm 4}(ax)\,{\rm d}x =\frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 4 a} \cdot \sin(2 ax)+\frac{\rm 1}{32 a}\cdot \sin(4 ax).$$ | :$$\int \sin^{\rm 4}(ax)\,{\rm d}x =\frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 4 a} \cdot \sin(2 ax)+\frac{\rm 1}{32 a}\cdot \sin(4 ax).$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - $y$ | + | - $y$ is limited to the range $0 \le y \le 1$ . |
| − | + $y$ | + | + $y$ is limited to the range $0 < y \le 1$ . |
| − | + | + | + The mean $m_y$ is less than the mean $m_x$. |
| − | { | + | {Calculate the mean of the random variable $y$. |
|type="{}"} | |type="{}"} | ||
| − | $m_y \ =$ | + | $m_y \ = \ $ { 0.849 3% } |
| − | { | + | {Calculate the the standard deviation of the random variable $y$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_y \ =$ | + | $\sigma_y \ = \ $ { 0.172 3% } |
| − | { | + | {Calculate the PDF $f_y(y)$. Note the symmetry properties. What PDF value results for $y = 0.6$? |
|type="{}"} | |type="{}"} | ||
| − | $f_y(y=0.6) \ =$ { 0.573 3% } | + | $f_y(y=0.6) \ = \ $ { 0.573 3% } |
| − | { | + | {What is the PDF value for $y = 1$? Interpret the result. What is the probability that $y$ is exactly equal $1$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(y=1) \ =$ { 0. } | + | ${\rm Pr}(y=1) \ = \ $ { 0. } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Correct are <u>the second and the third suggested solutions</u>: | |
| + | *Because of the range of values of $x$ and the given characteristic curve, $y$ cannot take values smaller than $0$ or larger than $1$ respectively. | ||
| + | *The value $y = 0$ cannot occur either, however, since neither $x = 0$ nor $x = 2$ are possible. | ||
| + | *With these properties, the result is surely $m_y < 1$, i.e., a smaller value than $m_x = 1$ (see specification). | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' To solve this task, one could, for example, first determine the PDF $f_y(y)$ and calculate $m_y$ from it in the usual way. | ||
| + | *The direct way leads to the same result: | ||
| + | :$$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$ | ||
| − | + | *With the current functions $g(x)$ and $f_x(x)$ we obtain: | |
| − | :$$ | + | :$$m_y=\int_{\rm 0}^{\rm 2}\hspace{-0.1cm}\sin^{\rm 3}({\pi}/{ 2}\cdot x)\,{\rm d}x=\frac{\rm 2}{\rm 3\cdot \pi}\cdot \cos^{\rm 3}({\pi}/{ 2}\cdot x)-\frac{\rm 2}{\rm \pi} \cdot \cos({3 \rm \pi}/{\rm 2}\cdot x)\Big|_{\rm 0}^{\rm 2}=\frac{\rm 8}{\rm 3\cdot \pi} \hspace{0.15cm}\underline{=\rm 0.849}.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' By analogy with point '''(2)''' holds: | |
| − | :$$\ | + | :$$m_{2 y}={\rm E}[y^{\rm 2}]={\rm E}[g^{\rm 2}( x)]=\int_{-\infty}^{+\infty}\hspace{-0.35cm}g^{2}( x)\cdot f_x(x)\,{\rm d}x.$$ |
| + | |||
| + | *This leads to the result: | ||
| + | :$$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0.15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\,{\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm | ||
0.75}.$$ | 0.75}.$$ | ||
| − | + | *With the result from '''(2)''' it thus follows for the standard deviation: | |
| − | :$$ | + | :$$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$ |
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Due to the symmetry of the PDF $f_x(x)$ and the characteristic curve $y =g(x)$ um $x = 1$ the two domains yield. | ||
| + | *$0 \le x \le 1$ and | ||
| + | *$1 \le x \le 2$ | ||
| + | |||
| + | |||
| + | each give the same contribution for $f_y(y)$. | ||
| + | *In the first domain, the derivative of the characteristic curve is positive: $g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x).$ | ||
| + | |||
| + | *The inverse function is: $ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$ | ||
| + | |||
| + | *Taking into account the second contribution by the factor $2$ we get the searched PDF in the range $0 \le y \le 1$: | ||
| + | :$$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$ | ||
| + | [[File:P_ID138__Sto_Z_3_9_e_neu.png|right|frame|PDF after transformation]] | ||
| + | *Outside of this range: $f_y(y) \equiv 0$. This leads to the intermediate result | ||
| + | :$$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}}.$$ | ||
| + | *And because of $\sin\big (\arcsin(y)\big) = y$: | ||
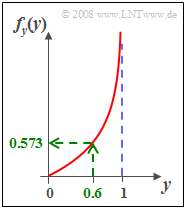
| + | :$$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}}.$$ | ||
| − | + | *At the point $y = 0.6$ one obtains the value $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$. | |
| − | + | *On the right, this PDF $f_y(y)$ is shown graphically. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(5)''' The PDF is infinitely large at the point $y = 1$. | |
| − | + | *This is due to the fact that at this point the derivative $g\hspace{0.05cm}'(x)$ of the characteristic curve runs horizontally. | |
| + | * However, since $y$ is a continuous random quantity, nevertheless ${\rm Pr}(y = 1) \hspace{0.15cm}\underline{= 0}$ holds. | ||
| − | |||
| − | : | + | This means: |
| + | *An infinity point in the PDF is not identical to a Dirac delta function. | ||
| + | *Or more casually expressed: An infinity point in the PDF is "less" than a Dirac delta function. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.6 Exponentially Distributed Random Variables^]] |
Latest revision as of 17:09, 17 February 2022
In this task, we consider a random variable $x$ with sine-square shaped $\rm PDF$ in the range between $x= 0$ and $x= 2$:
- $$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm for\hspace{0.25cm}{\rm 0\le \it x \le \rm 2} .$$
Outside of this, the PDF is identically zero.
The mean and the standard deviation of this random variable $x$ have already been determined in the Exercise 3.3:
- $$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$
Another random variable is obtained by transformation using the nonlinear characteristic curve
- $$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$
The figure shows in each case in the range $0 \le x \le 2$:
- above the PDF $f_x(x)$,
- below the nonlinear characteristic $y = g(x)$.
Hints:
- The exercise belongs to the chapter Exponentially Distributed Random Variables.
- In particular, reference is made to the section "Transformation of random variables" and the chapter "Expected Values and Moments".
- Given are the two indefinite integrals:
- $$\int \sin^{\rm 3}( ax)\,{\rm d}x = \frac{\rm 1}{ 3 a} \cdot \cos^{\rm 3}( ax)-\frac{\rm 1}{ a}\cdot \cos(ax),$$
- $$\int \sin^{\rm 4}(ax)\,{\rm d}x =\frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 4 a} \cdot \sin(2 ax)+\frac{\rm 1}{32 a}\cdot \sin(4 ax).$$
Questions
Solution
- Because of the range of values of $x$ and the given characteristic curve, $y$ cannot take values smaller than $0$ or larger than $1$ respectively.
- The value $y = 0$ cannot occur either, however, since neither $x = 0$ nor $x = 2$ are possible.
- With these properties, the result is surely $m_y < 1$, i.e., a smaller value than $m_x = 1$ (see specification).
(2) To solve this task, one could, for example, first determine the PDF $f_y(y)$ and calculate $m_y$ from it in the usual way.
- The direct way leads to the same result:
- $$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$
- With the current functions $g(x)$ and $f_x(x)$ we obtain:
- $$m_y=\int_{\rm 0}^{\rm 2}\hspace{-0.1cm}\sin^{\rm 3}({\pi}/{ 2}\cdot x)\,{\rm d}x=\frac{\rm 2}{\rm 3\cdot \pi}\cdot \cos^{\rm 3}({\pi}/{ 2}\cdot x)-\frac{\rm 2}{\rm \pi} \cdot \cos({3 \rm \pi}/{\rm 2}\cdot x)\Big|_{\rm 0}^{\rm 2}=\frac{\rm 8}{\rm 3\cdot \pi} \hspace{0.15cm}\underline{=\rm 0.849}.$$
(3) By analogy with point (2) holds:
- $$m_{2 y}={\rm E}[y^{\rm 2}]={\rm E}[g^{\rm 2}( x)]=\int_{-\infty}^{+\infty}\hspace{-0.35cm}g^{2}( x)\cdot f_x(x)\,{\rm d}x.$$
- This leads to the result:
- $$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0.15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\,{\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm 0.75}.$$
- With the result from (2) it thus follows for the standard deviation:
- $$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$
(4) Due to the symmetry of the PDF $f_x(x)$ and the characteristic curve $y =g(x)$ um $x = 1$ the two domains yield.
- $0 \le x \le 1$ and
- $1 \le x \le 2$
each give the same contribution for $f_y(y)$.
- In the first domain, the derivative of the characteristic curve is positive: $g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x).$
- The inverse function is: $ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$
- Taking into account the second contribution by the factor $2$ we get the searched PDF in the range $0 \le y \le 1$:
- $$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$
- Outside of this range: $f_y(y) \equiv 0$. This leads to the intermediate result
- $$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}}.$$
- And because of $\sin\big (\arcsin(y)\big) = y$:
- $$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}}.$$
- At the point $y = 0.6$ one obtains the value $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$.
- On the right, this PDF $f_y(y)$ is shown graphically.
(5) The PDF is infinitely large at the point $y = 1$.
- This is due to the fact that at this point the derivative $g\hspace{0.05cm}'(x)$ of the characteristic curve runs horizontally.
- However, since $y$ is a continuous random quantity, nevertheless ${\rm Pr}(y = 1) \hspace{0.15cm}\underline{= 0}$ holds.
This means:
- An infinity point in the PDF is not identical to a Dirac delta function.
- Or more casually expressed: An infinity point in the PDF is "less" than a Dirac delta function.