Difference between revisions of "Aufgaben:Exercise 4.07: Decision Boundaries once again"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} Datei:P_ID2016__Dig_Z_4_6.png|right|frame|Drei Signalraumkon…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
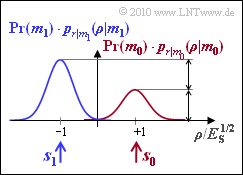
| − | [[File: | + | [[File:P_ID2017__Dig_A_4_7.png|right|frame|WDF mit ungleichen Symbolwahrscheinlichkeiten]] |
| + | Wir betrachten ein Übertragungssystem mit | ||
| + | * nur einer Basisfunktino ($N = 1$), | ||
| + | * zwei Signalen $s_0 = E_s^{\rm 1/2}$ und $s_1 = \, –E_s^{\rm 1/2} (M = 2)$, | ||
| + | * einem AWGN–Kanal mit Varianz $\sigma_n^2 = N_0/2$. | ||
| + | |||
| + | Da in dieser Aufgabe der allgemeine Fall ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$ behandelt wird, genügt es nicht, die bedingten Dichtefunktionen $p_{\it r|m_i}(\rho |m_i)$ zu betrachten. Vielmehr müssen diese noch mit den Symbolwahrscheinlichkeiten ${\rm Pr}(m_i)$ multipliziert weden (für $i$ sind hier die Werte $0$ und $1$ einzusetzen). | ||
| + | |||
| + | Liegt die Entscheidungsgrenze zwischen den beiden Regionen $I_0$ und $I_1$ bei $G = 0$, also in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$, so ist die Fehlerwahrscheinlichkeit unabhängig von den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$: | ||
| + | :$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei gibt $d$ den Abstand zwischen den Signalpunkten $s_0$ und $s_1$ an und $d/2$ dementsprechend den jeweiligen Abstand von $s_0$ bzw. $s_1$ von der Entscheidungsgrenze $G = 0$. Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist $\sigma_n$. | ||
| + | |||
| + | Sind dagegen die Auftrittswahrscheinlichkeiten unterschiedlich ⇒ ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, so kann durch eine Verschiebung der Entscheidergrenze $G$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden: | ||
| + | :$$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) | ||
| + | + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$ | ||
| + | |||
| + | wobei die Hilfsgröße $\gamma$ wie folgt definiert ist: | ||
| + | :$$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} | ||
| + | \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot E_{\rm S}^{1/2}\hspace{0.05cm}.$$ | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | ||
| + | * Die Werte der Q–Funktion können Sie mit folgendem Interaktionsmodul ermitteln: [[Komplementäre Gaußsche Fehlerfunktion]]. | ||
| + | |||
Revision as of 13:53, 7 November 2017
Wir betrachten ein Übertragungssystem mit
- nur einer Basisfunktino ($N = 1$),
- zwei Signalen $s_0 = E_s^{\rm 1/2}$ und $s_1 = \, –E_s^{\rm 1/2} (M = 2)$,
- einem AWGN–Kanal mit Varianz $\sigma_n^2 = N_0/2$.
Da in dieser Aufgabe der allgemeine Fall ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$ behandelt wird, genügt es nicht, die bedingten Dichtefunktionen $p_{\it r|m_i}(\rho |m_i)$ zu betrachten. Vielmehr müssen diese noch mit den Symbolwahrscheinlichkeiten ${\rm Pr}(m_i)$ multipliziert weden (für $i$ sind hier die Werte $0$ und $1$ einzusetzen).
Liegt die Entscheidungsgrenze zwischen den beiden Regionen $I_0$ und $I_1$ bei $G = 0$, also in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$, so ist die Fehlerwahrscheinlichkeit unabhängig von den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$
Hierbei gibt $d$ den Abstand zwischen den Signalpunkten $s_0$ und $s_1$ an und $d/2$ dementsprechend den jeweiligen Abstand von $s_0$ bzw. $s_1$ von der Entscheidungsgrenze $G = 0$. Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist $\sigma_n$.
Sind dagegen die Auftrittswahrscheinlichkeiten unterschiedlich ⇒ ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, so kann durch eine Verschiebung der Entscheidergrenze $G$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden:
- $$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$
wobei die Hilfsgröße $\gamma$ wie folgt definiert ist:
- $$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot E_{\rm S}^{1/2}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Die Werte der Q–Funktion können Sie mit folgendem Interaktionsmodul ermitteln: Komplementäre Gaußsche Fehlerfunktion.
Fragebogen
Musterlösung
(2)
(3)
(4)
(5)